2014. Longest Subsequence Repeated k Times

Description

You are given a string s of length n, and an integer k. You are tasked to find the longest subsequence repeated k times in string s.

A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.

A subsequence seq is repeated k times in the string s if seq * k is a subsequence of s, where seq * k represents a string constructed by concatenating seq k times.

• For example, "bba" is repeated 2 times in the string "bababcba", because the string "bbabba", constructed by concatenating "bba" 2 times, is a subsequence of the string "bababcba".

Return the longest subsequence repeated k times in string s. If multiple such subsequences are found, return the lexicographically largest one. If there is no such subsequence, return an empty string.

 

Example 1:

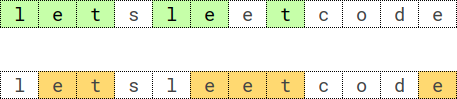
Input: s = "letsleetcode", k = 2
Output: "let"
Explanation: There are two longest subsequences repeated 2 times: "let" and "ete".
"let" is the lexicographically largest one.

Example 2:

Input: s = "bb", k = 2
Output: "b"
Explanation: The longest subsequence repeated 2 times is "b".

Example 3:

Input: s = "ab", k = 2
Output: ""
Explanation: There is no subsequence repeated 2 times. Empty string is returned.

 

Constraints:

• n == s.length
• 2 <= k <= 2000
• 2 <= n < min(2001, k * 8)
• s consists of lowercase English letters.

Solutions

Solution 1: BFS

We can first count the occurrences of each character in the string, and then store the characters that appear at least \(k\) times in a list \(\textit{cs}\) in ascending order. Next, we can use BFS to enumerate all possible subsequences.

We define a queue \(\textit{q}\), initially putting the empty string into the queue. Then, we take out a string \(\textit{cur}\) from the queue and try to append each character \(c \in \textit{cs}\) to the end of \(\textit{cur}\) to form a new string \(\textit{nxt}\). If \(\textit{nxt}\) is a subsequence that can be repeated \(k\) times, we add it to the answer and put \(\textit{nxt}\) back into the queue for further processing.

We need an auxiliary function \(\textit{check(t, k)}\) to determine whether the string \(\textit{t}\) is a repeated \(k\) times subsequence of string \(s\). Specifically, we can use two pointers to traverse \(s\) and \(\textit{t}\). If we can find all characters of \(\textit{t}\) in \(s\) and repeat this process \(k\) times, then return \(\textit{true}\); otherwise, return \(\textit{false}\).

Python3JavaC++GoTypeScript

class Solution:
    def longestSubsequenceRepeatedK(self, s: str, k: int) -> str:
        def check(t: str, k: int) -> bool:
            i = 0
            for c in s:
                if c == t[i]:
                    i += 1
                    if i == len(t):
                        k -= 1
                        if k == 0:
                            return True
                        i = 0
            return False

        cnt = Counter(s)
        cs = [c for c in ascii_lowercase if cnt[c] >= k]
        q = deque([""])
        ans = ""
        while q:
            cur = q.popleft()
            for c in cs:
                nxt = cur + c
                if check(nxt, k):
                    ans = nxt
                    q.append(nxt)
        return ans

class Solution {
    private char[] s;

    public String longestSubsequenceRepeatedK(String s, int k) {
        this.s = s.toCharArray();
        int[] cnt = new int[26];
        for (char c : this.s) {
            cnt[c - 'a']++;
        }

        List<Character> cs = new ArrayList<>();
        for (char c = 'a'; c <= 'z'; ++c) {
            if (cnt[c - 'a'] >= k) {
                cs.add(c);
            }
        }
        Deque<String> q = new ArrayDeque<>();
        q.offer("");
        String ans = "";
        while (!q.isEmpty()) {
            String cur = q.poll();
            for (char c : cs) {
                String nxt = cur + c;
                if (check(nxt, k)) {
                    ans = nxt;
                    q.offer(nxt);
                }
            }
        }
        return ans;
    }

    private boolean check(String t, int k) {
        int i = 0;
        for (char c : s) {
            if (c == t.charAt(i)) {
                i++;
                if (i == t.length()) {
                    if (--k == 0) {
                        return true;
                    }
                    i = 0;
                }
            }
        }
        return false;
    }
}

class Solution {
public:
    string longestSubsequenceRepeatedK(string s, int k) {
        auto check = [&](const string& t, int k) -> bool {
            int i = 0;
            for (char c : s) {
                if (c == t[i]) {
                    i++;
                    if (i == t.size()) {
                        if (--k == 0) {
                            return true;
                        }
                        i = 0;
                    }
                }
            }
            return false;
        };
        int cnt[26] = {};
        for (char c : s) {
            cnt[c - 'a']++;
        }

        vector<char> cs;
        for (char c = 'a'; c <= 'z'; ++c) {
            if (cnt[c - 'a'] >= k) {
                cs.push_back(c);
            }
        }

        queue<string> q;
        q.push("");
        string ans;
        while (!q.empty()) {
            string cur = q.front();
            q.pop();
            for (char c : cs) {
                string nxt = cur + c;
                if (check(nxt, k)) {
                    ans = nxt;
                    q.push(nxt);
                }
            }
        }
        return ans;
    }
};

func longestSubsequenceRepeatedK(s string, k int) string {
    check := func(t string, k int) bool {
        i := 0
        for _, c := range s {
            if byte(c) == t[i] {
                i++
                if i == len(t) {
                    k--
                    if k == 0 {
                        return true
                    }
                    i = 0
                }
            }
        }
        return false
    }

    cnt := [26]int{}
    for i := 0; i < len(s); i++ {
        cnt[s[i]-'a']++
    }

    cs := []byte{}
    for c := byte('a'); c <= 'z'; c++ {
        if cnt[c-'a'] >= k {
            cs = append(cs, c)
        }
    }

    q := []string{""}
    ans := ""
    for len(q) > 0 {
        cur := q[0]
        q = q[1:]
        for _, c := range cs {
            nxt := cur + string(c)
            if check(nxt, k) {
                ans = nxt
                q = append(q, nxt)
            }
        }
    }
    return ans
}

function longestSubsequenceRepeatedK(s: string, k: number): string {
    const check = (t: string, k: number): boolean => {
        let i = 0;
        for (const c of s) {
            if (c === t[i]) {
                i++;
                if (i === t.length) {
                    k--;
                    if (k === 0) {
                        return true;
                    }
                    i = 0;
                }
            }
        }
        return false;
    };

    const cnt = new Array(26).fill(0);
    for (const c of s) {
        cnt[c.charCodeAt(0) - 97]++;
    }

    const cs: string[] = [];
    for (let i = 0; i < 26; ++i) {
        if (cnt[i] >= k) {
            cs.push(String.fromCharCode(97 + i));
        }
    }

    const q: string[] = [''];
    let ans = '';
    while (q.length > 0) {
        const cur = q.shift()!;
        for (const c of cs) {
            const nxt = cur + c;
            if (check(nxt, k)) {
                ans = nxt;
                q.push(nxt);
            }
        }
    }

    return ans;
}

Comments