跳转至

654. 最大二叉树

难度中等

题目描述

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

  1. 创建一个根节点，其值为 nums 中的最大值。
  2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
  3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

 

示例 1：

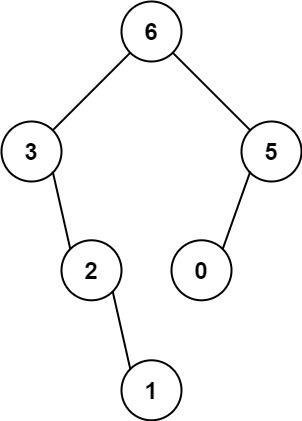
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

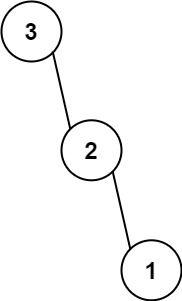
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

 

提示：

  • 1 <= nums.length <= 1000
  • 0 <= nums[i] <= 1000
  • nums 中的所有整数 互不相同

解法

方法一：递归

思考

根是区间最大值，左右递归同一规则。每次线性找最大值，最坏 \(O(n^2)\)，但 \(n\le 10^3\) 可通过。

对当前数组取 max 与下标，切开左右再递归即可对应定义。

先找到数组 \(nums\) 的最大元素所在的位置 \(i\)，将 \(nums[i]\) 作为根节点，然后递归左右两侧的子数组，构建左右子树。

时间复杂度 \(O(n^2)\)，空间复杂度 \(O(n)\)，其中 \(n\) 是数组的长度。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        def dfs(nums):
            if not nums:
                return None
            val = max(nums)
            i = nums.index(val)
            root = TreeNode(val)
            root.left = dfs(nums[:i])
            root.right = dfs(nums[i + 1 :])
            return root

        return dfs(nums)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int[] nums;

    public TreeNode constructMaximumBinaryTree(int[] nums) {
        this.nums = nums;
        return dfs(0, nums.length - 1);
    }

    private TreeNode dfs(int l, int r) {
        if (l > r) {
            return null;
        }
        int i = l;
        for (int j = l; j <= r; ++j) {
            if (nums[i] < nums[j]) {
                i = j;
            }
        }
        TreeNode root = new TreeNode(nums[i]);
        root.left = dfs(l, i - 1);
        root.right = dfs(i + 1, r);
        return root;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return dfs(nums, 0, nums.size() - 1);
    }

    TreeNode* dfs(vector<int>& nums, int l, int r) {
        if (l > r) return nullptr;
        int i = l;
        for (int j = l; j <= r; ++j) {
            if (nums[i] < nums[j]) {
                i = j;
            }
        }
        TreeNode* root = new TreeNode(nums[i]);
        root->left = dfs(nums, l, i - 1);
        root->right = dfs(nums, i + 1, r);
        return root;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func constructMaximumBinaryTree(nums []int) *TreeNode {
    var dfs func(l, r int) *TreeNode
    dfs = func(l, r int) *TreeNode {
        if l > r {
            return nil
        }
        i := l
        for j := l; j <= r; j++ {
            if nums[i] < nums[j] {
                i = j
            }
        }
        root := &TreeNode{Val: nums[i]}
        root.Left = dfs(l, i-1)
        root.Right = dfs(i+1, r)
        return root
    }
    return dfs(0, len(nums)-1)
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function constructMaximumBinaryTree(nums: number[]): TreeNode | null {
    const n = nums.length;
    if (n === 0) {
        return null;
    }
    const [val, i] = nums.reduce((r, v, i) => (r[0] < v ? [v, i] : r), [-1, 0]);
    return new TreeNode(
        val,
        constructMaximumBinaryTree(nums.slice(0, i)),
        constructMaximumBinaryTree(nums.slice(i + 1)),
    );
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    fn construct(nums: &Vec<i32>, start: usize, end: usize) -> Option<Rc<RefCell<TreeNode>>> {
        if start >= end {
            return None;
        }
        let mut idx = 0;
        let mut max_val = -1;
        for i in start..end {
            if nums[i] > max_val {
                idx = i;
                max_val = nums[i];
            }
        }
        Some(Rc::new(RefCell::new(TreeNode {
            val: max_val,
            left: Self::construct(nums, start, idx),
            right: Self::construct(nums, idx + 1, end),
        })))
    }

    pub fn construct_maximum_binary_tree(nums: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
        Self::construct(&nums, 0, nums.len())
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

struct TreeNode* construct(int* nums, int start, int end) {
    if (start >= end) {
        return NULL;
    }
    int idx = 0;
    int maxVal = -1;
    for (int i = start; i < end; i++) {
        if (nums[i] > maxVal) {
            idx = i;
            maxVal = nums[i];
        }
    }
    struct TreeNode* res = (struct TreeNode*) malloc(sizeof(struct TreeNode));
    res->val = maxVal;
    res->left = construct(nums, start, idx);
    res->right = construct(nums, idx + 1, end);
    return res;
}

struct TreeNode* constructMaximumBinaryTree(int* nums, int numsSize) {
    return construct(nums, 0, numsSize);
}

方法二：线段树

思考

方法一每次找最大值是线性。线段树把区间最大查询降到 \(O(\log n)\)，再按下标切开递归，总时间 \(O(n\log n)\)。

方法一中，每次查找区间最大值，需要 \(O(n)\) 的时间，我们可以借助线段树，将每次查询区间最大值的时间降至 \(O(\log n)\)。

最多需要查询 \(n\) 次，因此，总的时间复杂度为 \(O(n \times \log n)\)，空间复杂度 \(O(n)\)，其中 \(n\) 是数组的长度。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        def dfs(l, r):
            if l > r:
                return None
            val = tree.query(1, l, r)
            root = TreeNode(val)
            root.left = dfs(l, d[val] - 1)
            root.right = dfs(d[val] + 1, r)
            return root

        d = {v: i for i, v in enumerate(nums, 1)}
        tree = SegmentTree(nums)
        return dfs(1, len(nums))


class Node:
    def __init__(self):
        self.l = 0
        self.r = 0
        self.v = 0


class SegmentTree:
    def __init__(self, nums):
        self.nums = nums
        n = len(nums)
        self.tr = [Node() for _ in range(n << 2)]
        self.build(1, 1, n)

    def build(self, u, l, r):
        self.tr[u].l, self.tr[u].r = l, r
        if l == r:
            self.tr[u].v = self.nums[l - 1]
            return
        mid = (l + r) >> 1
        self.build(u << 1, l, mid)
        self.build(u << 1 | 1, mid + 1, r)
        self.pushup(u)

    def query(self, u, l, r):
        if self.tr[u].l >= l and self.tr[u].r <= r:
            return self.tr[u].v
        mid = (self.tr[u].l + self.tr[u].r) >> 1
        v = 0
        if l <= mid:
            v = max(v, self.query(u << 1, l, r))
        if r > mid:
            v = max(v, self.query(u << 1 | 1, l, r))
        return v

    def pushup(self, u):
        self.tr[u].v = max(self.tr[u << 1].v, self.tr[u << 1 | 1].v)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private SegmentTree tree;
    private int[] nums;
    private static int[] d = new int[1010];

    public TreeNode constructMaximumBinaryTree(int[] nums) {
        int n = nums.length;
        this.nums = nums;
        tree = new SegmentTree(nums);
        for (int i = 0; i < n; ++i) {
            d[nums[i]] = i + 1;
        }
        return dfs(1, n);
    }

    private TreeNode dfs(int l, int r) {
        if (l > r) {
            return null;
        }
        int val = tree.query(1, l, r);
        TreeNode root = new TreeNode(val);
        root.left = dfs(l, d[val] - 1);
        root.right = dfs(d[val] + 1, r);
        return root;
    }
}

class Node {
    int l;
    int r;
    int v;
}

class SegmentTree {
    Node[] tr;
    int[] nums;

    public SegmentTree(int[] nums) {
        int n = nums.length;
        this.nums = nums;
        tr = new Node[n << 2];
        for (int i = 0; i < tr.length; ++i) {
            tr[i] = new Node();
        }
        build(1, 1, n);
    }

    private void build(int u, int l, int r) {
        tr[u].l = l;
        tr[u].r = r;
        if (l == r) {
            tr[u].v = nums[l - 1];
            return;
        }
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    public int query(int u, int l, int r) {
        if (tr[u].l >= l && tr[u].r <= r) {
            return tr[u].v;
        }
        int mid = (tr[u].l + tr[u].r) >> 1;
        int v = 0;
        if (l <= mid) {
            v = query(u << 1, l, r);
        }
        if (r > mid) {
            v = Math.max(v, query(u << 1 | 1, l, r));
        }
        return v;
    }

    private void pushup(int u) {
        tr[u].v = Math.max(tr[u << 1].v, tr[u << 1 | 1].v);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Node {
public:
    int l, r, v;
};

class SegmentTree {
public:
    vector<Node*> tr;
    vector<int> nums;

    SegmentTree(vector<int>& nums) {
        this->nums = nums;
        int n = nums.size();
        tr.resize(n << 2);
        for (int i = 0; i < tr.size(); ++i) tr[i] = new Node();
        build(1, 1, n);
    }

    void build(int u, int l, int r) {
        tr[u]->l = l;
        tr[u]->r = r;
        if (l == r) {
            tr[u]->v = nums[l - 1];
            return;
        }
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    int query(int u, int l, int r) {
        if (tr[u]->l >= l && tr[u]->r <= r) return tr[u]->v;
        int mid = (tr[u]->l + tr[u]->r) >> 1;
        int v = 0;
        if (l <= mid) v = query(u << 1, l, r);
        if (r > mid) v = max(v, query(u << 1 | 1, l, r));
        return v;
    }

    void pushup(int u) {
        tr[u]->v = max(tr[u << 1]->v, tr[u << 1 | 1]->v);
    }
};

class Solution {
public:
    SegmentTree* tree;
    vector<int> nums;
    vector<int> d;

    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        tree = new SegmentTree(nums);
        this->nums = nums;
        d.assign(1010, 0);
        int n = nums.size();
        for (int i = 0; i < n; ++i) d[nums[i]] = i + 1;
        return dfs(1, nums.size());
    }

    TreeNode* dfs(int l, int r) {
        if (l > r) {
            return nullptr;
        }
        int val = tree->query(1, l, r);
        TreeNode* root = new TreeNode(val);
        root->left = dfs(l, d[val] - 1);
        root->right = dfs(d[val] + 1, r);
        return root;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func constructMaximumBinaryTree(nums []int) *TreeNode {
    d := make([]int, 1010)
    for i, v := range nums {
        d[v] = i + 1
    }
    tree := newSegmentTree(nums)
    var dfs func(l, r int) *TreeNode
    dfs = func(l, r int) *TreeNode {
        if l > r {
            return nil
        }
        val := tree.query(1, l, r)
        root := &TreeNode{Val: val}
        root.Left = dfs(l, d[val]-1)
        root.Right = dfs(d[val]+1, r)
        return root
    }

    return dfs(1, len(nums))
}

type node struct {
    l int
    r int
    v int
}

type segmentTree struct {
    nums []int
    tr   []*node
}

func newSegmentTree(nums []int) *segmentTree {
    n := len(nums)
    tr := make([]*node, n<<2)
    for i := range tr {
        tr[i] = &node{}
    }
    t := &segmentTree{nums, tr}
    t.build(1, 1, n)
    return t
}

func (t *segmentTree) build(u, l, r int) {
    t.tr[u].l, t.tr[u].r = l, r
    if l == r {
        t.tr[u].v = t.nums[l-1]
        return
    }
    mid := (l + r) >> 1
    t.build(u<<1, l, mid)
    t.build(u<<1|1, mid+1, r)
    t.pushup(u)
}

func (t *segmentTree) query(u, l, r int) int {
    if t.tr[u].l >= l && t.tr[u].r <= r {
        return t.tr[u].v
    }
    mid := (t.tr[u].l + t.tr[u].r) >> 1
    v := 0
    if l <= mid {
        v = t.query(u<<1, l, r)
    }
    if r > mid {
        v = max(v, t.query(u<<1|1, l, r))
    }
    return v
}

func (t *segmentTree) pushup(u int) {
    t.tr[u].v = max(t.tr[u<<1].v, t.tr[u<<1|1].v)
}

方法三：单调栈

思考

线段树仍要建树。从左到右扫，单调递减栈维护「左侧最近更大元」：弹出的最后节点成为当前左孩子，栈顶则把当前收为右孩子。一次入出栈即建完。

题目表达了一个意思：如果 \(nums\) 中间有一个数字 \(v\)，找出它左右两侧最大的数，这两个最大的数应该比 \(v\) 小。

了解单调栈的朋友，或许会注意到：

当我们尝试向栈中压入一个数字 \(v\) 时，如果栈顶元素比 \(v\) 小，则循环弹出栈顶元素，并记录最后一个弹出的元素 \(last\)。那么循环结束， \(last\) 必须位于 \(v\) 的左侧，因为 \(last\) 是 \(v\) 的左侧最大的数。令 \(node(val=v).left\) 指向 \(last\)。

如果此时存在栈顶元素，栈顶元素一定大于 \(v\)。 \(v\) 成为栈顶元素的候选右子树节点。令 \(stk.top().right\) 指向 \(v\)。然后 \(v\) 入栈。

遍历结束，栈底元素成为树的根节点。

时间复杂度 \(O(n)\)，空间复杂度 \(O(n)\)。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        stk = []
        for v in nums:
            node = TreeNode(v)
            last = None
            while stk and stk[-1].val < v:
                last = stk.pop()
            node.left = last
            if stk:
                stk[-1].right = node
            stk.append(node)
        return stk[0]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        Deque<TreeNode> stk = new ArrayDeque<>();
        for (int v : nums) {
            TreeNode node = new TreeNode(v);
            TreeNode last = null;
            while (!stk.isEmpty() && stk.peek().val < v) {
                last = stk.pop();
            }
            node.left = last;
            if (!stk.isEmpty()) {
                stk.peek().right = node;
            }
            stk.push(node);
        }
        return stk.getLast();
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        stack<TreeNode*> stk;
        for (int v : nums) {
            TreeNode* node = new TreeNode(v);
            TreeNode* last = nullptr;
            while (!stk.empty() && stk.top()->val < v) {
                last = stk.top();
                stk.pop();
            }
            node->left = last;
            if (!stk.empty()) {
                stk.top()->right = node;
            }
            stk.push(node);
        }
        while (stk.size() > 1) {
            stk.pop();
        }
        return stk.top();
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func constructMaximumBinaryTree(nums []int) *TreeNode {
    stk := []*TreeNode{}
    for _, v := range nums {
        node := &TreeNode{Val: v}
        var last *TreeNode
        for len(stk) > 0 && stk[len(stk)-1].Val < v {
            last = stk[len(stk)-1]
            stk = stk[:len(stk)-1]
        }
        node.Left = last
        if len(stk) > 0 {
            stk[len(stk)-1].Right = node
        }
        stk = append(stk, node)
    }
    return stk[0]
}

方法四：显式栈

思考

根是区间最大值，左右子树遵守同一规则。\(n \le 1000\)，每次线性扫描最大值是 \(O(n^2)\)，时间上可以通过。递增数组的最大值总在右端，第一次调用总是处理左侧剩下的 \(n-1\) 个元素，递归深度就是 \(n\)，会超出默认递归上限。

一段区间的根只由左右端点决定，不需要把子数组复制出来。

因此用下标区间 \([l, r)\) 表示当前段，栈里保存待建区间以及它挂在父节点的哪一侧。弹出区间后线性找出最大值建成节点，再把右区间和左区间压栈，左区间后进先出。空区间直接跳过。

在下标区间 \([l, r)\) 上线性找出最大值的下标 \(i\)，以 \(nums[i]\) 为根。左子树对应 \([l, i)\)，右子树对应 \([i + 1, r)\)。待建区间放在显式栈里：弹出一个区间后建好根，再把右区间和左区间压栈。空区间直接跳过。初始区间是 \([0, n)\)。

时间复杂度 \(O(n^2)\)，空间复杂度 \(O(n)\)，其中 \(n\) 是数组的长度。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        n = len(nums)
        root = None
        stk = [(0, n, None, 0)]
        while stk:
            l, r, parent, side = stk.pop()
            if l >= r:
                continue
            i = l
            for j in range(l + 1, r):
                if nums[j] > nums[i]:
                    i = j
            node = TreeNode(nums[i])
            if parent is None:
                root = node
            elif side == 0:
                parent.left = node
            else:
                parent.right = node
            stk.append((i + 1, r, node, 1))
            stk.append((l, i, node, 0))
        return root

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        int n = nums.length;
        TreeNode root = null;
        Deque<Frame> stk = new ArrayDeque<>();
        stk.push(new Frame(0, n - 1, null, 0));
        while (!stk.isEmpty()) {
            Frame cur = stk.pop();
            if (cur.l > cur.r) {
                continue;
            }
            int i = cur.l;
            for (int j = cur.l; j <= cur.r; ++j) {
                if (nums[i] < nums[j]) {
                    i = j;
                }
            }
            TreeNode node = new TreeNode(nums[i]);
            if (cur.parent == null) {
                root = node;
            } else if (cur.side == 0) {
                cur.parent.left = node;
            } else {
                cur.parent.right = node;
            }
            stk.push(new Frame(i + 1, cur.r, node, 1));
            stk.push(new Frame(cur.l, i - 1, node, 0));
        }
        return root;
    }

    private static class Frame {
        int l, r, side;
        TreeNode parent;

        Frame(int l, int r, TreeNode parent, int side) {
            this.l = l;
            this.r = r;
            this.parent = parent;
            this.side = side;
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        struct Frame {
            int l, r, side;
            TreeNode* parent;
        };
        int n = nums.size();
        TreeNode* root = nullptr;
        vector<Frame> stk{{0, n - 1, 0, nullptr}};
        while (!stk.empty()) {
            auto cur = stk.back();
            stk.pop_back();
            if (cur.l > cur.r) {
                continue;
            }
            int i = cur.l;
            for (int j = cur.l; j <= cur.r; ++j) {
                if (nums[i] < nums[j]) {
                    i = j;
                }
            }
            TreeNode* node = new TreeNode(nums[i]);
            if (cur.parent == nullptr) {
                root = node;
            } else if (cur.side == 0) {
                cur.parent->left = node;
            } else {
                cur.parent->right = node;
            }
            stk.push_back({i + 1, cur.r, 1, node});
            stk.push_back({cur.l, i - 1, 0, node});
        }
        return root;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func constructMaximumBinaryTree(nums []int) *TreeNode {
    type frame struct {
        l, r, side int
        parent     *TreeNode
    }
    n := len(nums)
    var root *TreeNode
    stk := []frame{{0, n - 1, 0, nil}}
    for len(stk) > 0 {
        cur := stk[len(stk)-1]
        stk = stk[:len(stk)-1]
        if cur.l > cur.r {
            continue
        }
        i := cur.l
        for j := cur.l; j <= cur.r; j++ {
            if nums[j] > nums[i] {
                i = j
            }
        }
        node := &TreeNode{Val: nums[i]}
        if cur.parent == nil {
            root = node
        } else if cur.side == 0 {
            cur.parent.Left = node
        } else {
            cur.parent.Right = node
        }
        stk = append(stk, frame{i + 1, cur.r, 1, node}, frame{cur.l, i - 1, 0, node})
    }
    return root
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function constructMaximumBinaryTree(nums: number[]): TreeNode | null {
    const n = nums.length;
    let root: TreeNode | null = null;
    const stk: [number, number, TreeNode | null, number][] = [[0, n, null, 0]];
    while (stk.length) {
        const [l, r, parent, side] = stk.pop()!;
        if (l >= r) {
            continue;
        }
        let i = l;
        for (let j = l + 1; j < r; ++j) {
            if (nums[j] > nums[i]) {
                i = j;
            }
        }
        const node = new TreeNode(nums[i]);
        if (parent === null) {
            root = node;
        } else if (side === 0) {
            parent.left = node;
        } else {
            parent.right = node;
        }
        stk.push([i + 1, r, node, 1]);
        stk.push([l, i, node, 0]);
    }
    return root;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    pub fn construct_maximum_binary_tree(nums: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
        let n = nums.len();
        let mut root: Option<Rc<RefCell<TreeNode>>> = None;
        let mut stk: Vec<(usize, usize, Option<Rc<RefCell<TreeNode>>>, u8)> = vec![(0, n, None, 0)];
        while let Some((l, r, parent, side)) = stk.pop() {
            if l >= r {
                continue;
            }
            let mut idx = l;
            for i in l + 1..r {
                if nums[i] > nums[idx] {
                    idx = i;
                }
            }
            let node = Rc::new(RefCell::new(TreeNode {
                val: nums[idx],
                left: None,
                right: None,
            }));
            if let Some(p) = parent {
                if side == 0 {
                    p.borrow_mut().left = Some(Rc::clone(&node));
                } else {
                    p.borrow_mut().right = Some(Rc::clone(&node));
                }
            } else {
                root = Some(Rc::clone(&node));
            }
            stk.push((idx + 1, r, Some(Rc::clone(&node)), 1));
            stk.push((l, idx, Some(Rc::clone(&node)), 0));
        }
        root
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

struct TreeNode* constructMaximumBinaryTree(int* nums, int numsSize) {
    typedef struct {
        int l, r, side;
        struct TreeNode* parent;
    } Frame;
    Frame* stk = (Frame*) malloc(sizeof(Frame) * (numsSize * 2 + 5));
    int top = 0;
    stk[top++] = (Frame) {0, numsSize, 0, NULL};
    struct TreeNode* root = NULL;
    while (top) {
        Frame cur = stk[--top];
        if (cur.l >= cur.r) {
            continue;
        }
        int idx = cur.l;
        for (int i = cur.l + 1; i < cur.r; ++i) {
            if (nums[i] > nums[idx]) {
                idx = i;
            }
        }
        struct TreeNode* node = (struct TreeNode*) malloc(sizeof(struct TreeNode));
        node->val = nums[idx];
        node->left = node->right = NULL;
        if (cur.parent == NULL) {
            root = node;
        } else if (cur.side == 0) {
            cur.parent->left = node;
        } else {
            cur.parent->right = node;
        }
        stk[top++] = (Frame) {idx + 1, cur.r, 1, node};
        stk[top++] = (Frame) {cur.l, idx, 0, node};
    }
    free(stk);
    return root;
}

方法五：线段树 + 显式栈

思考

方法一已经用显式栈按区间最大值建树，但每次找最大值仍是线性扫描。线段树把区间最大查询降到 \(O(\log n)\)。左区间仍可能连成 \(n\) 层，所以切开左右子树也放在同一个显式栈上，总时间 \(O(n \log n)\)。

方法一中，每次查找区间最大值，需要 \(O(n)\) 的时间，我们可以借助线段树，将每次查询区间最大值的时间降至 \(O(\log n)\)。左右子树的区间放进显式栈，弹出时用线段树取出该区间的最大值并建节点。

最多需要查询 \(n\) 次，因此，总的时间复杂度为 \(O(n \times \log n)\)，空间复杂度 \(O(n)\)，其中 \(n\) 是数组的长度。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        d = {v: i for i, v in enumerate(nums, 1)}
        tree = SegmentTree(nums)
        root = None
        stk = [(1, len(nums), None, 0)]
        while stk:
            l, r, parent, side = stk.pop()
            if l > r:
                continue
            val = tree.query(1, l, r)
            node = TreeNode(val)
            i = d[val]
            if parent is None:
                root = node
            elif side == 0:
                parent.left = node
            else:
                parent.right = node
            stk.append((i + 1, r, node, 1))
            stk.append((l, i - 1, node, 0))
        return root


class Node:
    def __init__(self):
        self.l = 0
        self.r = 0
        self.v = 0


class SegmentTree:
    def __init__(self, nums):
        self.nums = nums
        n = len(nums)
        self.tr = [Node() for _ in range(n << 2)]
        self.build(1, 1, n)

    def build(self, u, l, r):
        self.tr[u].l, self.tr[u].r = l, r
        if l == r:
            self.tr[u].v = self.nums[l - 1]
            return
        mid = (l + r) >> 1
        self.build(u << 1, l, mid)
        self.build(u << 1 | 1, mid + 1, r)
        self.pushup(u)

    def query(self, u, l, r):
        if self.tr[u].l >= l and self.tr[u].r <= r:
            return self.tr[u].v
        mid = (self.tr[u].l + self.tr[u].r) >> 1
        v = 0
        if l <= mid:
            v = max(v, self.query(u << 1, l, r))
        if r > mid:
            v = max(v, self.query(u << 1 | 1, l, r))
        return v

    def pushup(self, u):
        self.tr[u].v = max(self.tr[u << 1].v, self.tr[u << 1 | 1].v)

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private SegmentTree tree;
    private int[] nums;
    private static int[] d = new int[1010];

    public TreeNode constructMaximumBinaryTree(int[] nums) {
        int n = nums.length;
        this.nums = nums;
        tree = new SegmentTree(nums);
        for (int i = 0; i < n; ++i) {
            d[nums[i]] = i + 1;
        }
        TreeNode root = null;
        Deque<Frame> stk = new ArrayDeque<>();
        stk.push(new Frame(1, n, null, 0));
        while (!stk.isEmpty()) {
            Frame cur = stk.pop();
            if (cur.l > cur.r) {
                continue;
            }
            int val = tree.query(1, cur.l, cur.r);
            TreeNode node = new TreeNode(val);
            if (cur.parent == null) {
                root = node;
            } else if (cur.side == 0) {
                cur.parent.left = node;
            } else {
                cur.parent.right = node;
            }
            int i = d[val];
            stk.push(new Frame(i + 1, cur.r, node, 1));
            stk.push(new Frame(cur.l, i - 1, node, 0));
        }
        return root;
    }

    private static class Frame {
        int l, r, side;
        TreeNode parent;

        Frame(int l, int r, TreeNode parent, int side) {
            this.l = l;
            this.r = r;
            this.parent = parent;
            this.side = side;
        }
    }
}

class Node {
    int l;
    int r;
    int v;
}

class SegmentTree {
    Node[] tr;
    int[] nums;

    public SegmentTree(int[] nums) {
        int n = nums.length;
        this.nums = nums;
        tr = new Node[n << 2];
        for (int i = 0; i < tr.length; ++i) {
            tr[i] = new Node();
        }
        build(1, 1, n);
    }

    private void build(int u, int l, int r) {
        tr[u].l = l;
        tr[u].r = r;
        if (l == r) {
            tr[u].v = nums[l - 1];
            return;
        }
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    public int query(int u, int l, int r) {
        if (tr[u].l >= l && tr[u].r <= r) {
            return tr[u].v;
        }
        int mid = (tr[u].l + tr[u].r) >> 1;
        int v = 0;
        if (l <= mid) {
            v = query(u << 1, l, r);
        }
        if (r > mid) {
            v = Math.max(v, query(u << 1 | 1, l, r));
        }
        return v;
    }

    private void pushup(int u) {
        tr[u].v = Math.max(tr[u << 1].v, tr[u << 1 | 1].v);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Node {
public:
    int l, r, v;
};

class SegmentTree {
public:
    vector<Node*> tr;
    vector<int> nums;

    SegmentTree(vector<int>& nums) {
        this->nums = nums;
        int n = nums.size();
        tr.resize(n << 2);
        for (int i = 0; i < tr.size(); ++i) tr[i] = new Node();
        build(1, 1, n);
    }

    void build(int u, int l, int r) {
        tr[u]->l = l;
        tr[u]->r = r;
        if (l == r) {
            tr[u]->v = nums[l - 1];
            return;
        }
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    int query(int u, int l, int r) {
        if (tr[u]->l >= l && tr[u]->r <= r) return tr[u]->v;
        int mid = (tr[u]->l + tr[u]->r) >> 1;
        int v = 0;
        if (l <= mid) v = query(u << 1, l, r);
        if (r > mid) v = max(v, query(u << 1 | 1, l, r));
        return v;
    }

    void pushup(int u) {
        tr[u]->v = max(tr[u << 1]->v, tr[u << 1 | 1]->v);
    }
};

class Solution {
public:
    SegmentTree* tree;
    vector<int> nums;
    vector<int> d;

    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        tree = new SegmentTree(nums);
        this->nums = nums;
        d.assign(1010, 0);
        int n = nums.size();
        for (int i = 0; i < n; ++i) d[nums[i]] = i + 1;
        struct Frame {
            int l, r, side;
            TreeNode* parent;
        };
        TreeNode* root = nullptr;
        vector<Frame> stk{{1, n, 0, nullptr}};
        while (!stk.empty()) {
            auto cur = stk.back();
            stk.pop_back();
            if (cur.l > cur.r) {
                continue;
            }
            int val = tree->query(1, cur.l, cur.r);
            TreeNode* node = new TreeNode(val);
            if (cur.parent == nullptr) {
                root = node;
            } else if (cur.side == 0) {
                cur.parent->left = node;
            } else {
                cur.parent->right = node;
            }
            int i = d[val];
            stk.push_back({i + 1, cur.r, 1, node});
            stk.push_back({cur.l, i - 1, 0, node});
        }
        return root;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func constructMaximumBinaryTree(nums []int) *TreeNode {
    d := make([]int, 1010)
    for i, v := range nums {
        d[v] = i + 1
    }
    tree := newSegmentTree(nums)
    type frame struct {
        l, r, side int
        parent     *TreeNode
    }
    var root *TreeNode
    stk := []frame{{1, len(nums), 0, nil}}
    for len(stk) > 0 {
        cur := stk[len(stk)-1]
        stk = stk[:len(stk)-1]
        if cur.l > cur.r {
            continue
        }
        val := tree.query(1, cur.l, cur.r)
        node := &TreeNode{Val: val}
        if cur.parent == nil {
            root = node
        } else if cur.side == 0 {
            cur.parent.Left = node
        } else {
            cur.parent.Right = node
        }
        i := d[val]
        stk = append(stk, frame{i + 1, cur.r, 1, node}, frame{cur.l, i - 1, 0, node})
    }
    return root
}

type node struct {
    l int
    r int
    v int
}

type segmentTree struct {
    nums []int
    tr   []*node
}

func newSegmentTree(nums []int) *segmentTree {
    n := len(nums)
    tr := make([]*node, n<<2)
    for i := range tr {
        tr[i] = &node{}
    }
    t := &segmentTree{nums, tr}
    t.build(1, 1, n)
    return t
}

func (t *segmentTree) build(u, l, r int) {
    t.tr[u].l, t.tr[u].r = l, r
    if l == r {
        t.tr[u].v = t.nums[l-1]
        return
    }
    mid := (l + r) >> 1
    t.build(u<<1, l, mid)
    t.build(u<<1|1, mid+1, r)
    t.pushup(u)
}

func (t *segmentTree) query(u, l, r int) int {
    if t.tr[u].l >= l && t.tr[u].r <= r {
        return t.tr[u].v
    }
    mid := (t.tr[u].l + t.tr[u].r) >> 1
    v := 0
    if l <= mid {
        v = t.query(u<<1, l, r)
    }
    if r > mid {
        v = max(v, t.query(u<<1|1, l, r))
    }
    return v
}

func (t *segmentTree) pushup(u int) {
    t.tr[u].v = max(t.tr[u<<1].v, t.tr[u<<1|1].v)
}

评论