
题目描述
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:
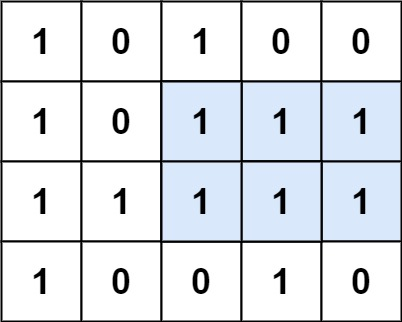
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:6
解释:最大矩形如上图所示。
示例 2:
输入:matrix = [["0"]]
输出:0
示例 3:
输入:matrix = [["1"]]
输出:1
提示:
rows == matrix.lengthcols == matrix[0].length1 <= rows, cols <= 200matrix[i][j] 为 '0' 或 '1'
解法
方法一:单调栈
我们把每一行视为柱状图的底部,对每一行求柱状图的最大面积即可。
具体地,我们维护一个与矩阵列数相同的数组 \(\textit{heights}\),其中 \(\textit{heights}[j]\) 表示以当前行为底部、以第 \(j\) 列为高度的柱子的高度。对于每一行,我们遍历每一列:
- 如果当前元素为 '1',则将 \(\textit{heights}[j]\) 加 \(1\)。
- 如果当前元素为 '0',则将 \(\textit{heights}[j]\) 置为 \(0\)。
然后,我们使用单调栈算法计算当前柱状图的最大矩形面积,并更新答案。
单调栈的具体做法如下:
- 初始化一个空栈 \(\textit{stk}\),用于存储柱子的索引。
- 初始化两个数组 \(\textit{left}\) 和 \(\textit{right}\),分别表示每个柱子左侧和右侧第一个小于当前柱子的柱子的索引。
- 遍历柱子高度数组 \(\textit{heights}\),首先计算每个柱子左侧第一个小于当前柱子的柱子的索引,并存储在 \(\textit{left}\) 中。
- 然后反向遍历柱子高度数组 \(\textit{heights}\),计算每个柱子右侧第一个小于当前柱子的柱子的索引,并存储在 \(\textit{right}\) 中。
- 最后,计算每个柱子的最大矩形面积,并更新答案。
时间复杂度 \(O(m \times n)\),其中 \(m\) 表示 \(matrix\) 的行数,\(n\) 表示 \(matrix\) 的列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | class Solution:
def maximalRectangle(self, matrix: List[List[str]]) -> int:
heights = [0] * len(matrix[0])
ans = 0
for row in matrix:
for j, v in enumerate(row):
if v == "1":
heights[j] += 1
else:
heights[j] = 0
ans = max(ans, self.largestRectangleArea(heights))
return ans
def largestRectangleArea(self, heights: List[int]) -> int:
n = len(heights)
stk = []
left = [-1] * n
right = [n] * n
for i, h in enumerate(heights):
while stk and heights[stk[-1]] >= h:
stk.pop()
if stk:
left[i] = stk[-1]
stk.append(i)
stk = []
for i in range(n - 1, -1, -1):
h = heights[i]
while stk and heights[stk[-1]] >= h:
stk.pop()
if stk:
right[i] = stk[-1]
stk.append(i)
return max(h * (right[i] - left[i] - 1) for i, h in enumerate(heights))
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 | class Solution {
public int maximalRectangle(char[][] matrix) {
int n = matrix[0].length;
int[] heights = new int[n];
int ans = 0;
for (var row : matrix) {
for (int j = 0; j < n; ++j) {
if (row[j] == '1') {
heights[j] += 1;
} else {
heights[j] = 0;
}
}
ans = Math.max(ans, largestRectangleArea(heights));
}
return ans;
}
private int largestRectangleArea(int[] heights) {
int res = 0, n = heights.length;
Deque<Integer> stk = new ArrayDeque<>();
int[] left = new int[n];
int[] right = new int[n];
Arrays.fill(right, n);
for (int i = 0; i < n; ++i) {
while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) {
right[stk.pop()] = i;
}
left[i] = stk.isEmpty() ? -1 : stk.peek();
stk.push(i);
}
for (int i = 0; i < n; ++i) {
res = Math.max(res, heights[i] * (right[i] - left[i] - 1));
}
return res;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 | class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
int n = matrix[0].size();
vector<int> heights(n);
int ans = 0;
for (auto& row : matrix) {
for (int j = 0; j < n; ++j) {
if (row[j] == '1')
++heights[j];
else
heights[j] = 0;
}
ans = max(ans, largestRectangleArea(heights));
}
return ans;
}
int largestRectangleArea(vector<int>& heights) {
int res = 0, n = heights.size();
stack<int> stk;
vector<int> left(n, -1);
vector<int> right(n, n);
for (int i = 0; i < n; ++i) {
while (!stk.empty() && heights[stk.top()] >= heights[i]) {
right[stk.top()] = i;
stk.pop();
}
if (!stk.empty()) left[i] = stk.top();
stk.push(i);
}
for (int i = 0; i < n; ++i)
res = max(res, heights[i] * (right[i] - left[i] - 1));
return res;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | func maximalRectangle(matrix [][]byte) int {
n := len(matrix[0])
heights := make([]int, n)
ans := 0
for _, row := range matrix {
for j, v := range row {
if v == '1' {
heights[j]++
} else {
heights[j] = 0
}
}
ans = max(ans, largestRectangleArea(heights))
}
return ans
}
func largestRectangleArea(heights []int) int {
res, n := 0, len(heights)
var stk []int
left, right := make([]int, n), make([]int, n)
for i := range right {
right[i] = n
}
for i, h := range heights {
for len(stk) > 0 && heights[stk[len(stk)-1]] >= h {
right[stk[len(stk)-1]] = i
stk = stk[:len(stk)-1]
}
if len(stk) > 0 {
left[i] = stk[len(stk)-1]
} else {
left[i] = -1
}
stk = append(stk, i)
}
for i, h := range heights {
res = max(res, h*(right[i]-left[i]-1))
}
return res
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | function maximalRectangle(matrix: string[][]): number {
const n = matrix[0].length;
const heights: number[] = new Array(n).fill(0);
let ans = 0;
for (const row of matrix) {
for (let j = 0; j < n; ++j) {
if (row[j] === '1') {
heights[j] += 1;
} else {
heights[j] = 0;
}
}
ans = Math.max(ans, largestRectangleArea(heights));
}
return ans;
}
function largestRectangleArea(heights: number[]): number {
let res = 0;
const n = heights.length;
const stk: number[] = [];
const left: number[] = new Array(n);
const right: number[] = new Array(n).fill(n);
for (let i = 0; i < n; ++i) {
while (stk.length && heights[stk[stk.length - 1]] >= heights[i]) {
right[stk.pop()!] = i;
}
left[i] = stk.length === 0 ? -1 : stk[stk.length - 1];
stk.push(i);
}
for (let i = 0; i < n; ++i) {
res = Math.max(res, heights[i] * (right[i] - left[i] - 1));
}
return res;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 | impl Solution {
pub fn maximal_rectangle(matrix: Vec<Vec<char>>) -> i32 {
let n = matrix[0].len();
let mut heights = vec![0; n];
let mut ans = 0;
for row in matrix {
for j in 0..n {
if row[j] == '1' {
heights[j] += 1;
} else {
heights[j] = 0;
}
}
ans = ans.max(Self::largest_rectangle_area(&heights));
}
ans
}
fn largest_rectangle_area(heights: &Vec<i32>) -> i32 {
let mut res = 0;
let n = heights.len();
let mut stk: Vec<usize> = Vec::new();
let mut left = vec![0; n];
let mut right = vec![n; n];
for i in 0..n {
while let Some(&top) = stk.last() {
if heights[top] >= heights[i] {
right[top] = i;
stk.pop();
} else {
break;
}
}
left[i] = if stk.is_empty() { -1 } else { stk[stk.len() - 1] as i32 };
stk.push(i);
}
for i in 0..n {
res = res.max(heights[i] * (right[i] as i32 - left[i] - 1));
}
res
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 | public class Solution {
public int MaximalRectangle(char[][] matrix) {
int n = matrix[0].Length;
int[] heights = new int[n];
int ans = 0;
foreach (var row in matrix) {
for (int j = 0; j < n; ++j) {
if (row[j] == '1') {
heights[j] += 1;
} else {
heights[j] = 0;
}
}
ans = Math.Max(ans, LargestRectangleArea(heights));
}
return ans;
}
private int LargestRectangleArea(int[] heights) {
int res = 0, n = heights.Length;
Stack<int> stk = new Stack<int>();
int[] left = new int[n];
int[] right = new int[n];
Array.Fill(right, n);
for (int i = 0; i < n; ++i) {
while (stk.Count > 0 && heights[stk.Peek()] >= heights[i]) {
right[stk.Pop()] = i;
}
left[i] = stk.Count == 0 ? -1 : stk.Peek();
stk.Push(i);
}
for (int i = 0; i < n; ++i) {
res = Math.Max(res, heights[i] * (right[i] - left[i] - 1));
}
return res;
}
}
|

