
题目描述
给你一个由 X-Y 平面上的点组成的数组 points ,其中 points[i] = [xi, yi] 。从其中取任意三个不同的点组成三角形,返回能组成的最大三角形的面积。与真实值误差在 10-5 内的答案将会视为正确答案。
示例 1:
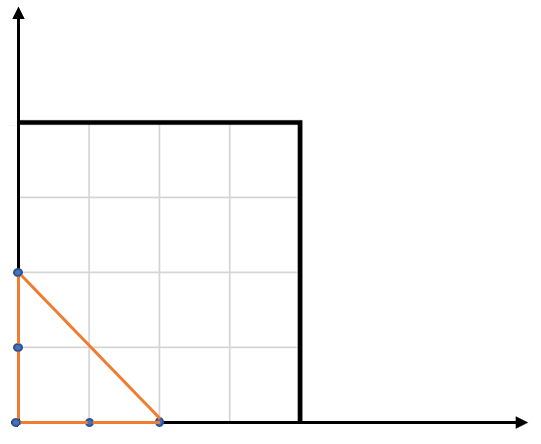
输入:points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出:2.00000
解释:输入中的 5 个点如上图所示,红色的三角形面积最大。
示例 2:
输入:points = [[1,0],[0,0],[0,1]]
输出:0.50000
提示:
3 <= points.length <= 50-50 <= xi, yi <= 50- 给出的所有点 互不相同
解法
方法一:枚举三点面积公式
给定平面上三点 \((x_1, y_1)\), \((x_2, y_2)\), \((x_3, y_3)\),其面积公式为:
\[S = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_1 - x_1y_3 - x_2y_1 - x_3y_2 \right|\]
我们可以枚举所有的三点组合,计算面积的最大值。
时间复杂度 \(O(n^3)\),其中 \(n\) 是点的数量。空间复杂度 \(O(1)\)。
| class Solution:
def largestTriangleArea(self, points: List[List[int]]) -> float:
ans = 0
for x1, y1 in points:
for x2, y2 in points:
for x3, y3 in points:
u1, v1 = x2 - x1, y2 - y1
u2, v2 = x3 - x1, y3 - y1
t = abs(u1 * v2 - u2 * v1) / 2
ans = max(ans, t)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | class Solution {
public double largestTriangleArea(int[][] points) {
double ans = 0;
for (int[] p1 : points) {
int x1 = p1[0], y1 = p1[1];
for (int[] p2 : points) {
int x2 = p2[0], y2 = p2[1];
for (int[] p3 : points) {
int x3 = p3[0], y3 = p3[1];
int u1 = x2 - x1, v1 = y2 - y1;
int u2 = x3 - x1, v2 = y3 - y1;
double t = Math.abs(u1 * v2 - u2 * v1) / 2.0;
ans = Math.max(ans, t);
}
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution {
public:
double largestTriangleArea(vector<vector<int>>& points) {
double ans = 0;
for (auto& p1 : points) {
int x1 = p1[0], y1 = p1[1];
for (auto& p2 : points) {
int x2 = p2[0], y2 = p2[1];
for (auto& p3 : points) {
int x3 = p3[0], y3 = p3[1];
int u1 = x2 - x1, v1 = y2 - y1;
int u2 = x3 - x1, v2 = y3 - y1;
double t = abs(u1 * v2 - u2 * v1) / 2.0;
ans = max(ans, t);
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | func largestTriangleArea(points [][]int) float64 {
ans := 0.0
for _, p1 := range points {
x1, y1 := p1[0], p1[1]
for _, p2 := range points {
x2, y2 := p2[0], p2[1]
for _, p3 := range points {
x3, y3 := p3[0], p3[1]
u1, v1 := x2-x1, y2-y1
u2, v2 := x3-x1, y3-y1
t := float64(abs(u1*v2-u2*v1)) / 2.0
ans = math.Max(ans, t)
}
}
}
return ans
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | function largestTriangleArea(points: number[][]): number {
let ans = 0;
for (const [x1, y1] of points) {
for (const [x2, y2] of points) {
for (const [x3, y3] of points) {
const u1 = x2 - x1,
v1 = y2 - y1;
const u2 = x3 - x1,
v2 = y3 - y1;
const t = Math.abs(u1 * v2 - u2 * v1) / 2;
ans = Math.max(ans, t);
}
}
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | impl Solution {
pub fn largest_triangle_area(points: Vec<Vec<i32>>) -> f64 {
let mut ans: f64 = 0.0;
for point1 in &points {
let (x1, y1) = (point1[0], point1[1]);
for point2 in &points {
let (x2, y2) = (point2[0], point2[1]);
for point3 in &points {
let (x3, y3) = (point3[0], point3[1]);
let u1 = x2 - x1;
let v1 = y2 - y1;
let u2 = x3 - x1;
let v2 = y3 - y1;
let t = ((u1 * v2 - u2 * v1) as f64).abs() / 2.0;
ans = ans.max(t);
}
}
}
ans
}
}
|

