二叉搜索树 二叉树 树
题目描述 给定二叉搜索树(BST)的根节点root 和一个整数值val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回null 。
示例 1:
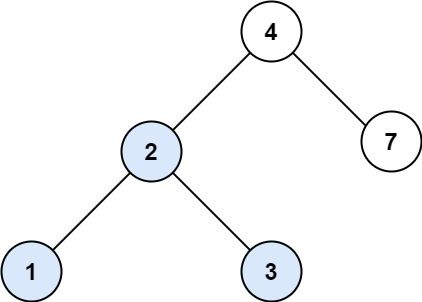
输入: root = [4,2,7,1,3], val = 2
输出: [2,1,3]
示例 2:
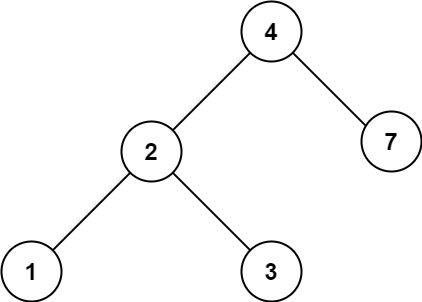
输入: root = [4,2,7,1,3], val = 5
输出: []
提示:
树中节点数在 [1, 5000] 范围内 1 <= Node.val <= 107 root 是二叉搜索树1 <= val <= 107 解法 方法一:递归 我们判断当前节点是否为空或者当前节点的值是否等于目标值,如果是则返回当前节点。
否则,如果当前节点的值大于目标值,则递归搜索左子树,否则递归搜索右子树。
时间复杂度 \(O(n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 是二叉树的节点数。
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def searchBST ( self , root : Optional [ TreeNode ], val : int ) -> Optional [ TreeNode ]:
if root is None or root . val == val :
return root
return (
self . searchBST ( root . left , val )
if root . val > val
else self . searchBST ( root . right , val )
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode searchBST ( TreeNode root , int val ) {
if ( root == null || root . val == val ) {
return root ;
}
return root . val > val ? searchBST ( root . left , val ) : searchBST ( root . right , val );
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
TreeNode * searchBST ( TreeNode * root , int val ) {
if ( ! root || root -> val == val ) {
return root ;
}
return root -> val > val ? searchBST ( root -> left , val ) : searchBST ( root -> right , val );
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func searchBST ( root * TreeNode , val int ) * TreeNode {
if root == nil || root . Val == val {
return root
}
if root . Val > val {
return searchBST ( root . Left , val )
}
return searchBST ( root . Right , val )
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function searchBST ( root : TreeNode | null , val : number ) : TreeNode | null {
if ( root === null || root . val === val ) {
return root ;
}
return root . val > val ? searchBST ( root . left , val ) : searchBST ( root . right , val );
}
GitHub