
题目描述
给定一个下标从 0 到 n - 1 的 n 个节点的 无向图。该图由 m 条边组成,用一个二维整数数组 edges 表示,其中 edges[i] = [ui, vi, wi] 表示节点 ui 和 vi 之间有一条修复成本为 wi 的边。
同时给定一个整数 k。一开始,所有 边都是被损坏的。
你可以选择一个非负整数 money并修复所有修复成本 小于或等于 money 的边。其他所有边保持损坏状态,无法使用。
你想要从节点 0 出发,使用最多 k 条边到达节点 n - 1。
返回一个整数,表示实现此目标所需的 最小 成本,如果不可能则返回 -1。
示例 1:
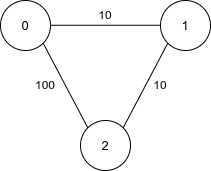
输入:n = 3, edges = [[0,1,10],[1,2,10],[0,2,100]], k = 1
输出:100
解释:
唯一使用最多 k = 1 条边的合法路径是 0 -> 2,这需要花费 100 来修复边。因此,所需的最低成本是 100。
示例 2:
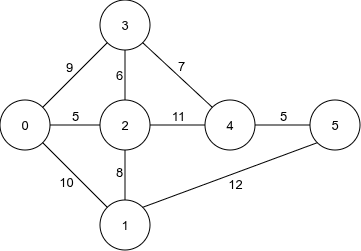
输入:n = 6, edges = [[0,2,5],[2,3,6],[3,4,7],[4,5,5],[0,1,10],[1,5,12],[0,3,9],[1,2,8],[2,4,11]], k = 2
输出:12
解释:
- 由于
money = 12,所有修复成本不超过 12 的边都变得可用。 - 这使得存在路径
0 -> 1 -> 5,使用恰好 2 条边到达节点 5。 - 如果
money < 12,不存在从节点 0 到节点 5 长度最多为 k = 2 的合法路径。 - 因此,所需的最少成本是 12。
示例 3:

输入:n = 3, edges = [[0,1,1]], k = 1
输出:-1
解释:
从节点 0 无法使用任何金额到达节点 2。因此,答案是 -1。
提示:
2 <= n <= 5 * 1041 <= edges.length == m <= 105edges[i] = [ui, vi, wi]0 <= ui, vi < n1 <= wi <= 1091 <= k <= n- 图中没有自环或重复边。
解法
方法一:二分查找 + BFS
我们注意到,修复边的成本越高,可用的边就越多,越容易满足从节点 \(0\) 出发,使用最多 \(k\) 条边到达节点 \(n - 1\) 的要求。并且,最小的修复成本一定在 \(\textit{edges}\) 中,因此,我们先对 \(\textit{edges}\) 按照修复成本进行排序,然后使用二分查找来寻找满足要求的最小修复成本。
我们二分枚举修复成本的下标,定义左边界 \(l = 0\),右边界 \(r = |\textit{edges}| - 1\)。对于中间位置 \(mid = \lfloor (l + r) / 2 \rfloor\),我们将修复成本小于等于 \(\textit{edges}[mid][2]\) 的边加入图中,然后使用 BFS 判断从节点 \(0\) 出发,是否可以使用最多 \(k\) 条边到达节点 \(n - 1\)。如果可以,则将右边界更新为 \(r = mid\);否则,将左边界更新为 \(l = mid + 1\)。当二分查找结束后,我们需要再进行一次 BFS 判断 \(\textit{edges}[l][2]\) 是否满足要求,如果满足则返回 \(\textit{edges}[l][2]\),否则返回 \(-1\)。
时间复杂度 \(O((m + n) \times \log m)\),空间复杂度 \(O(n)\)。其中 \(n\) 和 \(m\) 分别是节点数和边数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 | class Solution:
def minCost(self, n: int, edges: List[List[int]], k: int) -> int:
def check(idx: int) -> bool:
g = [[] for _ in range(n)]
for u, v, _ in edges[: idx + 1]:
g[u].append(v)
g[v].append(u)
q = [0]
dist = 0
vis = [False] * n
vis[0] = True
while q:
nq = []
for u in q:
if u == n - 1:
return dist <= k
for v in g[u]:
if not vis[v]:
vis[v] = True
nq.append(v)
q = nq
dist += 1
return False
m = len(edges)
edges.sort(key=lambda x: x[2])
l, r = 0, m - 1
while l < r:
mid = (l + r) >> 1
if check(mid):
r = mid
else:
l = mid + 1
return edges[l][2] if check(l) else -1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54 | class Solution {
private int n;
private int[][] edges;
private int k;
public int minCost(int n, int[][] edges, int k) {
this.n = n;
this.edges = edges;
this.k = k;
Arrays.sort(edges, (a, b) -> a[2] - b[2]);
int l = 0, r = edges.length - 1;
while (l < r) {
int mid = (l + r) >> 1;
if (check(mid)) {
r = mid;
} else {
l = mid + 1;
}
}
return check(l) ? edges[l][2] : -1;
}
private boolean check(int idx) {
List<Integer>[] g = new List[n];
Arrays.setAll(g, i -> new ArrayList<>());
for (int i = 0; i <= idx; ++i) {
int u = edges[i][0], v = edges[i][1];
g[u].add(v);
g[v].add(u);
}
List<Integer> q = new ArrayList<>();
q.add(0);
int dist = 0;
boolean[] vis = new boolean[n];
vis[0] = true;
while (!q.isEmpty()) {
List<Integer> nq = new ArrayList<>();
for (int u : q) {
if (u == n - 1) {
return dist <= k;
}
for (int v : g[u]) {
if (!vis[v]) {
vis[v] = true;
nq.add(v);
}
}
}
q = nq;
++dist;
}
return false;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54 | class Solution {
public:
int minCost(int n, vector<vector<int>>& edges, int k) {
sort(edges.begin(), edges.end(),
[](const vector<int>& a, const vector<int>& b) {
return a[2] < b[2];
});
auto check = [&](int idx) -> bool {
vector<vector<int>> g(n);
for (int i = 0; i <= idx; ++i) {
int u = edges[i][0], v = edges[i][1];
g[u].push_back(v);
g[v].push_back(u);
}
vector<int> q;
q.push_back(0);
vector<char> vis(n, 0);
vis[0] = 1;
int dist = 0;
while (!q.empty()) {
vector<int> nq;
for (int u : q) {
if (u == n - 1) {
return dist <= k;
}
for (int v : g[u]) {
if (!vis[v]) {
vis[v] = 1;
nq.push_back(v);
}
}
}
q.swap(nq);
++dist;
}
return false;
};
int m = edges.size();
int l = 0, r = m - 1;
while (l < r) {
int mid = (l + r) >> 1;
if (check(mid)) {
r = mid;
} else {
l = mid + 1;
}
}
return check(l) ? edges[l][2] : -1;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53 | func minCost(n int, edges [][]int, k int) int {
sort.Slice(edges, func(i, j int) bool {
return edges[i][2] < edges[j][2]
})
check := func(idx int) bool {
g := make([][]int, n)
for i := 0; i <= idx; i++ {
u, v := edges[i][0], edges[i][1]
g[u] = append(g[u], v)
g[v] = append(g[v], u)
}
q := make([]int, 0, n)
q = append(q, 0)
vis := make([]bool, n)
vis[0] = true
dist := 0
for len(q) > 0 {
nq := make([]int, 0)
for _, u := range q {
if u == n-1 {
return dist <= k
}
for _, v := range g[u] {
if !vis[v] {
vis[v] = true
nq = append(nq, v)
}
}
}
q = nq
dist++
}
return false
}
m := len(edges)
l, r := 0, m-1
for l < r {
mid := (l + r) >> 1
if check(mid) {
r = mid
} else {
l = mid + 1
}
}
if check(l) {
return edges[l][2]
}
return -1
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 | function minCost(n: number, edges: number[][], k: number): number {
edges.sort((a, b) => a[2] - b[2]);
const check = (idx: number): boolean => {
const g: number[][] = Array.from({ length: n }, () => []);
for (let i = 0; i <= idx; i++) {
const [u, v] = edges[i];
g[u].push(v);
g[v].push(u);
}
let q: number[] = [0];
const vis: boolean[] = Array(n).fill(false);
vis[0] = true;
let dist = 0;
while (q.length > 0) {
const nq: number[] = [];
for (const u of q) {
if (u === n - 1) {
return dist <= k;
}
for (const v of g[u]) {
if (!vis[v]) {
vis[v] = true;
nq.push(v);
}
}
}
q = nq;
dist++;
}
return false;
};
let [l, r] = [0, edges.length - 1];
while (l < r) {
const mid = (l + r) >> 1;
if (check(mid)) {
r = mid;
} else {
l = mid + 1;
}
}
return check(l) ? edges[l][2] : -1;
}
|



