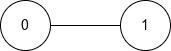题目描述
给定一棵编号从 0 到 n - 1 的有 n 个节点 无向树。它通过一个长度为 n - 1 的二维整数数组 edges 给出,其中 edges[i] = [ai, bi] 表示树中的 ai 和 bi 节点之间有一条边。
如果一个节点是树的任何 直径路径 的 端点,则称其为 特殊 节点。
返回一个长度为 n 的二进制字符串 s,其中如果节点 i 是特殊的,则 s[i] = '1',否则 s[i] = '0'。
一棵树的 直径路径 是任意两个节点之间的 最长 简单路径。一棵树可能有多个直径路径。
路径的 端点 是该路径上的 第一个 或 最后一个 节点。
示例 1:

输入:n = 3, edges = [[0,1],[1,2]]
输出:"101"
解释:
- 这棵树的直径包含 2 个节点。
- 唯一的直径路径是从节点 0 到节点 2 的路径。
- 这条路径的端点是节点 0 和 2,因此它们是特殊的。
示例 2:
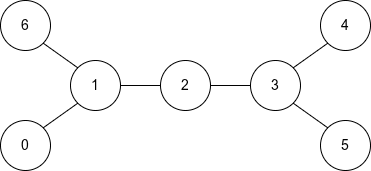
输入:n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[3,5],[1,6]]
输出:"1000111"
解释:
这棵树的直径由 4 条边组成。有 4 条直径路径:
- 从节点 0 到节点 4 的路径
- 从节点 0 到节点 5 的路径
- 从节点 6 到节点 4 的路径
- 从节点 6 到节点 5 的路径
特殊节点是节点 0, 4, 5, 6,因为它们至少在一个直径路径中是端点。
示例 3:
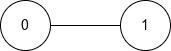
输入:n = 2, edges = [[0,1]]
输出:"11"
解释:
- 这棵树的直径由 1 条边组成。
- 唯一的直径路径是从节点 0 到节点 1 的路径
- 这条路径的端点是节点 0 和节点 1,因此它们是特殊的。
提示:
2 <= n <= 105edges.length == n - 1edges[i] = [ai, bi]0 <= ai, bi < n- 输入保证
edges 表示一棵合法的树。
解法
方法一:BFS
我们首先将数组 \(\text{edges}\) 转换为邻接表表示的无向图,其中 \(g[u]\) 表示与节点 \(u\) 相邻的所有节点。
接下来,我们可以使用广度优先搜索(BFS)来找到树的直径端点。具体步骤如下:
- 从任意节点(例如节点 \(0\))开始,使用 BFS 找到距离该节点最远的节点 \(a\)。
- 从节点 \(a\) 开始,再次使用 BFS 找到距离节点 \(a\) 最远的节点 \(b\),以及从节点 \(a\) 到所有其他节点的距离数组 \(\text{dist1}\)。
- 从节点 \(b\) 开始,使用 BFS 找到从节点 \(b\) 到所有其他节点的距离数组 \(\text{dist2}\)。
- 树的直径长度为 \(\text{dist1}[b]\)。对于每个节点 \(i\),如果 \(\text{dist1}[i]\) 或 \(\text{dist2}[i]\) 等于直径长度,则节点 \(i\) 是特殊节点。
时间复杂度 \(O(n)\),空间复杂度 \(O(n)\)。其中 \(n\) 为节点的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | class Solution:
def findSpecialNodes(self, n: int, edges: List[List[int]]) -> str:
g = [[] for _ in range(n)]
for a, b in edges:
g[a].append(b)
g[b].append(a)
def bfs(start: int):
dist = [-1] * n
dist[start] = 0
q = deque([start])
far = start
while q:
u = q.popleft()
if dist[u] > dist[far]:
far = u
for v in g[u]:
if dist[v] == -1:
dist[v] = dist[u] + 1
q.append(v)
return far, dist
a, _ = bfs(0)
b, dist1 = bfs(a)
_, dist2 = bfs(b)
d = dist1[b]
ans = ["0"] * n
for i in range(n):
if dist1[i] == d or dist2[i] == d:
ans[i] = "1"
return "".join(ans)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52 | class Solution {
public String findSpecialNodes(int n, int[][] edges) {
List<Integer>[] g = new ArrayList[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (int[] e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
record BFSResult(int far, int[] dist) {
}
IntFunction<BFSResult> bfs = (int start) -> {
int[] dist = new int[n];
Arrays.fill(dist, -1);
dist[start] = 0;
ArrayDeque<Integer> q = new ArrayDeque<>();
q.add(start);
int far = start;
while (!q.isEmpty()) {
int u = q.poll();
if (dist[u] > dist[far]) {
far = u;
}
for (int v : g[u]) {
if (dist[v] == -1) {
dist[v] = dist[u] + 1;
q.add(v);
}
}
}
return new BFSResult(far, dist);
};
int a = bfs.apply(0).far();
BFSResult r1 = bfs.apply(a);
int b = r1.far();
int[] dist1 = r1.dist();
int[] dist2 = bfs.apply(b).dist();
int d = dist1[b];
char[] ans = new char[n];
Arrays.fill(ans, '0');
for (int i = 0; i < n; i++) {
if (dist1[i] == d || dist2[i] == d) {
ans[i] = '1';
}
}
return new String(ans);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 | class Solution {
public:
string findSpecialNodes(int n, vector<vector<int>>& edges) {
vector<vector<int>> g(n);
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
auto bfs = [&](int start) -> pair<int, vector<int>> {
vector<int> dist(n, -1);
dist[start] = 0;
deque<int> q;
q.push_back(start);
int far = start;
while (!q.empty()) {
int u = q.front();
q.pop_front();
if (dist[u] > dist[far]) {
far = u;
}
for (int v : g[u]) {
if (dist[v] == -1) {
dist[v] = dist[u] + 1;
q.push_back(v);
}
}
}
return {far, dist};
};
auto [a, _0] = bfs(0);
auto [b, dist1] = bfs(a);
auto [_1, dist2] = bfs(b);
int d = dist1[b];
string ans(n, '0');
for (int i = 0; i < n; i++) {
if (dist1[i] == d || dist2[i] == d) {
ans[i] = '1';
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48 | func findSpecialNodes(n int, edges [][]int) string {
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
bfs := func(start int) (int, []int) {
dist := make([]int, n)
for i := range dist {
dist[i] = -1
}
dist[start] = 0
q := make([]int, 0, n)
q = append(q, start)
far := start
for head := 0; head < len(q); head++ {
u := q[head]
if dist[u] > dist[far] {
far = u
}
for _, v := range g[u] {
if dist[v] == -1 {
dist[v] = dist[u] + 1
q = append(q, v)
}
}
}
return far, dist
}
a, _ := bfs(0)
b, dist1 := bfs(a)
_, dist2 := bfs(b)
d := dist1[b]
ans := make([]byte, n)
for i := range ans {
ans[i] = '0'
}
for i := 0; i < n; i++ {
if dist1[i] == d || dist2[i] == d {
ans[i] = '1'
}
}
return string(ans)
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | function findSpecialNodes(n: number, edges: number[][]): string {
const g: number[][] = Array.from({ length: n }, () => []);
for (const [a, b] of edges) {
g[a].push(b);
g[b].push(a);
}
const bfs = (start: number): [number, number[]] => {
const dist = new Array<number>(n).fill(-1);
dist[start] = 0;
const q: number[] = [start];
let far = start;
for (const u of q) {
if (dist[u] > dist[far]) {
far = u;
}
for (const v of g[u]) {
if (dist[v] === -1) {
dist[v] = dist[u] + 1;
q.push(v);
}
}
}
return [far, dist];
};
const [a] = bfs(0);
const [b, dist1] = bfs(a);
const [, dist2] = bfs(b);
const d = dist1[b];
const ans: string[] = new Array(n).fill('0');
for (let i = 0; i < n; i++) {
if (dist1[i] === d || dist2[i] === d) {
ans[i] = '1';
}
}
return ans.join('');
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49 | use std::collections::VecDeque;
impl Solution {
pub fn find_special_nodes(n: i32, edges: Vec<Vec<i32>>) -> String {
let n = n as usize;
let mut g: Vec<Vec<usize>> = vec![vec![]; n];
for e in edges {
let a = e[0] as usize;
let b = e[1] as usize;
g[a].push(b);
g[b].push(a);
}
fn bfs(start: usize, g: &Vec<Vec<usize>>) -> (usize, Vec<i32>) {
let n = g.len();
let mut dist = vec![-1i32; n];
let mut q: VecDeque<usize> = VecDeque::new();
dist[start] = 0;
q.push_back(start);
let mut far = start;
while let Some(u) = q.pop_front() {
if dist[u] > dist[far] {
far = u;
}
for &v in &g[u] {
if dist[v] == -1 {
dist[v] = dist[u] + 1;
q.push_back(v);
}
}
}
(far, dist)
}
let (a, _) = bfs(0, &g);
let (b, dist1) = bfs(a, &g);
let (_, dist2) = bfs(b, &g);
let d = dist1[b];
let mut ans = vec![b'0'; n];
for i in 0..n {
if dist1[i] == d || dist2[i] == d {
ans[i] = b'1';
}
}
String::from_utf8(ans).unwrap()
}
}
|