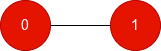3772. 树中子图的最大得分
题目描述
给你一个 无向树 ,它包含 n 个节点,编号从 0 到 n - 1。树由一个长度为 n - 1 的二维整数数组 edges 描述,其中 edges[i] = [ai, bi] 表示在节点 ai 和节点 bi 之间有一条边。
另给你一个长度为 n 的整数数组 good,其中 good[i] 为 1 表示第 i 个节点是好节点,为 0 表示它是坏节点。
定义 子图 的 得分 为子图中好节点的数量减去坏节点的数量。
对于每个节点 i,找到包含节点 i 的所有 连通子图 中可能的最大得分。
返回一个长度为 n 的整数数组,其中第 i 个元素是节点 i 的 最大得分 。
子图 是原图的一个子集,其顶点和边均来自原图。
连通子图 是一个子图,其中每一对顶点都可以通过该子图的边相互到达。
示例 1:
输入: n = 3, edges = [[0,1],[1,2]], good = [1,0,1]
输出: [1,1,1]
解释:
- 绿色节点是好节点,红色节点是坏节点。
- 对于每个节点,包含它的最佳连通子图是整棵树,该树有 2 个好节点和 1 个坏节点,得分为 1。
- 包含某个节点的其他连通子图可能有相同的得分。
示例 2:
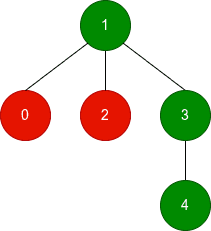
输入: n = 5, edges = [[1,0],[1,2],[1,3],[3,4]], good = [0,1,0,1,1]
输出: [2,3,2,3,3]
解释:
- 节点 0:最佳连通子图由节点
0, 1, 3, 4组成,其中有 3 个好节点和 1 个坏节点,得分为3 - 1 = 2。 - 节点 1、3 和 4:最佳连通子图由节点
1, 3, 4组成,其中有 3 个好节点,得分为 3。 - 节点 2:最佳连通子图由节点
1, 2, 3, 4组成,其中有 3 个好节点和 1 个坏节点,得分为3 - 1 = 2。
示例 3:
输入: n = 2, edges = [[0,1]], good = [0,0]
输出: [-1,-1]
解释:
对于每个节点,包含另一节点只会增加一个坏节点,因此每个节点的最佳得分为 -1。
提示:
2 <= n <= 105edges.length == n - 1edges[i] = [ai, bi]0 <= ai, bi < ngood.length == n0 <= good[i] <= 1- 输入保证
edges表示一棵有效树。
解法
方法一
1 | |
1 | |
1 | |
1 | |