3623. 统计梯形的数目 I

题目描述

给你一个二维整数数组 points，其中 points[i] = [x_i, y_i] 表示第 i 个点在笛卡尔平面上的坐标。

水平梯形 是一种凸四边形，具有 至少一对 水平边（即平行于 x 轴的边）。两条直线平行当且仅当它们的斜率相同。

返回可以从 points 中任意选择四个不同点组成的 水平梯形 数量。

由于答案可能非常大，请返回结果对 10⁹ + 7 取余数后的值。

示例 1：

输入： points = [[1,0],[2,0],[3,0],[2,2],[3,2]]

输出： 3

解释：

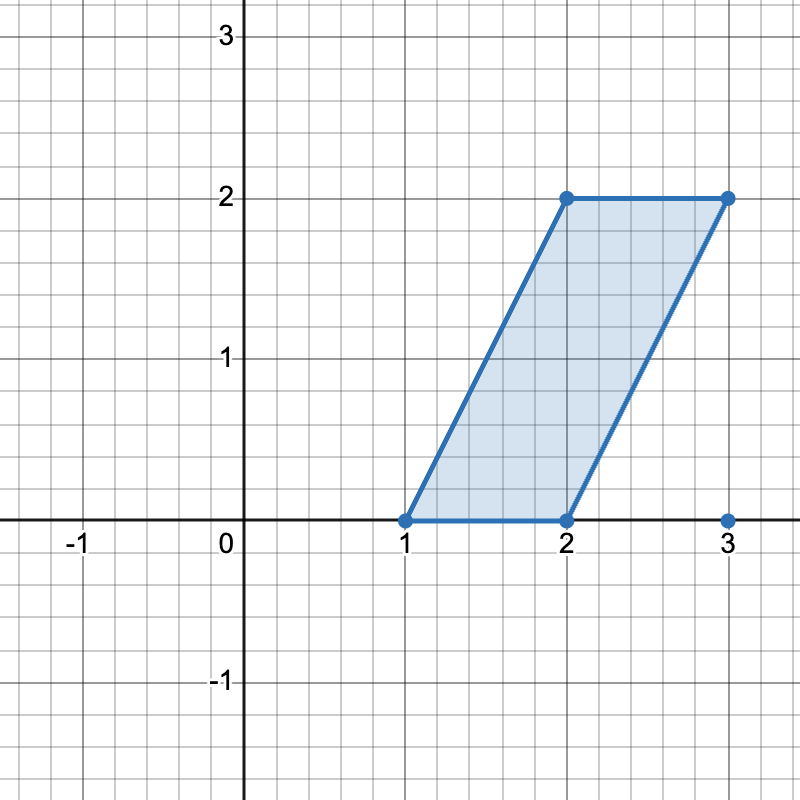
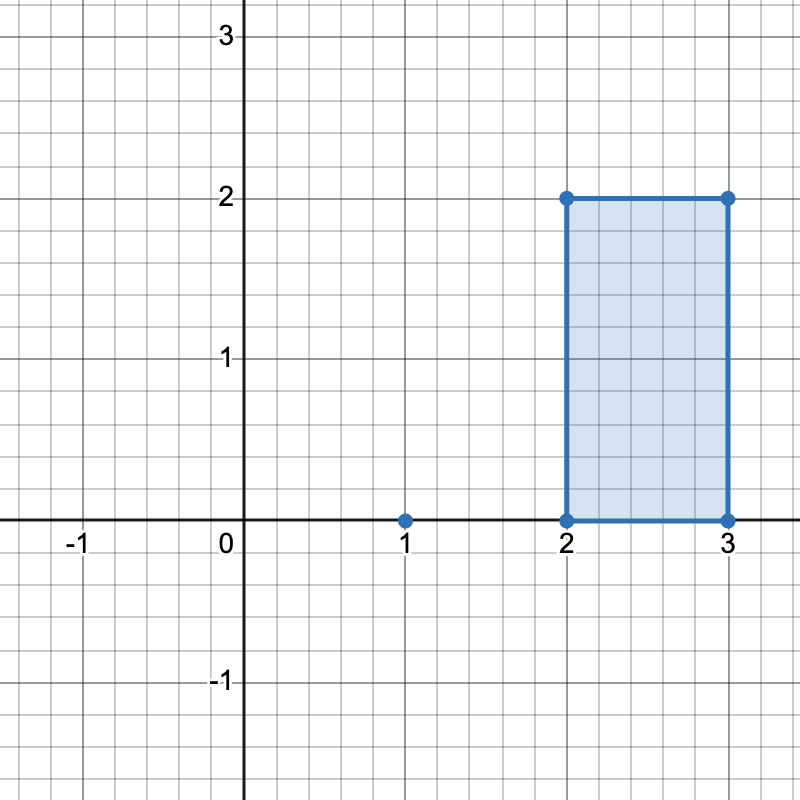
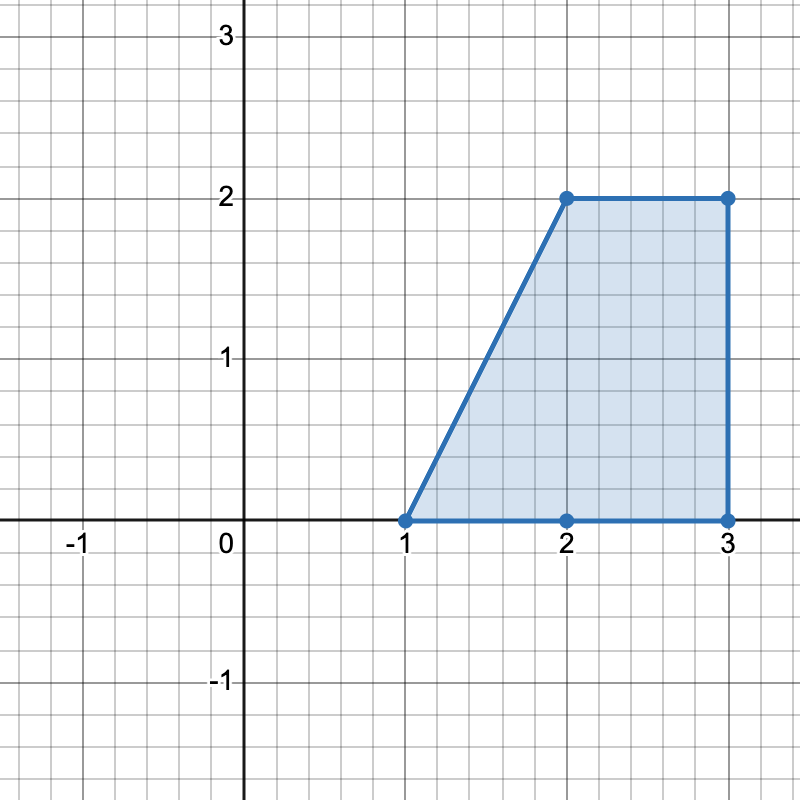
有三种不同方式选择四个点组成一个水平梯形：

使用点 [1,0]、[2,0]、[3,2] 和 [2,2]。
使用点 [2,0]、[3,0]、[3,2] 和 [2,2]。
使用点 [1,0]、[3,0]、[3,2] 和 [2,2]。

示例 2：

输入： points = [[0,0],[1,0],[0,1],[2,1]]

输出： 1

解释：

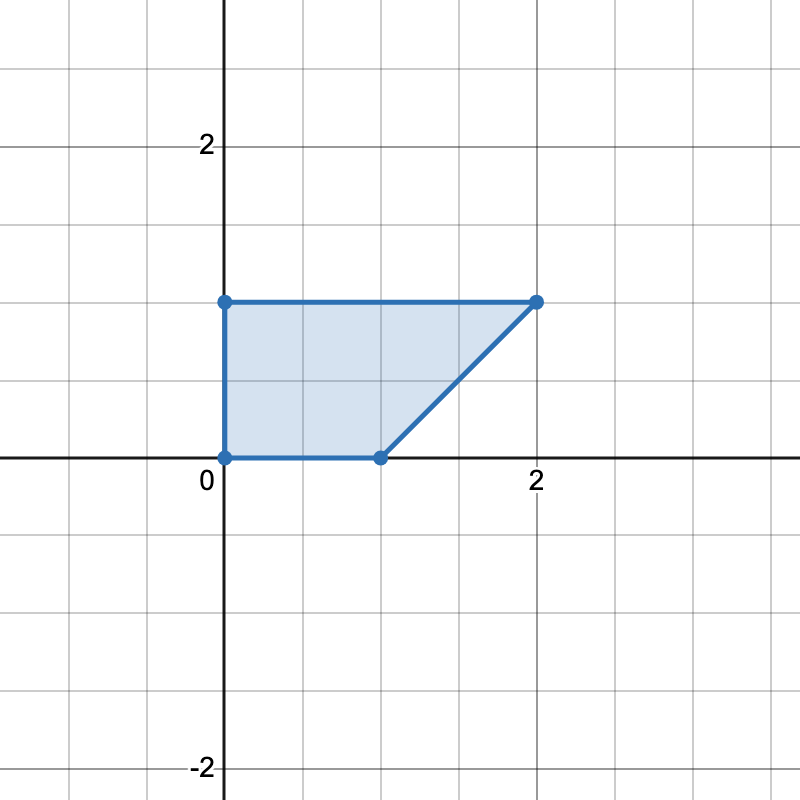
只有一种方式可以组成一个水平梯形。

提示：

4 <= points.length <= 10⁵
–10⁸ <= x_i, y_i <= 10⁸
所有点两两不同。

解法

方法一：枚举

根据题目描述，水平边满足 \(y\) 坐标相同，因此我们可以根据 \(y\) 坐标将点进行分组，统计每个 \(y\) 坐标对应的点的数量。

我们用一个哈希表 \(\textit{cnt}\) 来存储每个 \(y\) 坐标对应的点的数量。对于每个 \(y\) 坐标 \(y_i\)，假设对应的点的数量为 \(v\)，那么从这些点中选择两点作为水平边的方式有 \(\binom{v}{2} = \frac{v(v-1)}{2}\) 种，记为 \(t\)。

我们用一个变量 \(s\) 来记录之前所有 \(y\) 坐标对应的水平边的数量之和。那么，我们可以将当前 \(y\) 坐标对应的水平边的数量 \(t\) 与之前所有 \(y\) 坐标对应的水平边的数量之和 \(s\) 相乘，得到以当前 \(y\) 坐标为一对水平边的梯形的数量，并将其累加到答案中。最后，我们将当前 \(y\) 坐标对应的水平边的数量 \(t\) 累加到 \(s\) 中，以便后续计算。

注意，由于答案可能非常大，我们需要对 \(10^9 + 7\) 取余数。

时间复杂度 \(O(n)\)，空间复杂度 \(O(n)\)。其中 \(n\) 是点的数量。

Python3JavaC++GoTypeScript

class Solution:
    def countTrapezoids(self, points: List[List[int]]) -> int:
        mod = 10**9 + 7
        cnt = Counter(p[1] for p in points)
        ans = s = 0
        for v in cnt.values():
            t = v * (v - 1) // 2
            ans = (ans + s * t) % mod
            s += t
        return ans

class Solution {
    public int countTrapezoids(int[][] points) {
        final int mod = (int) 1e9 + 7;
        Map<Integer, Integer> cnt = new HashMap<>();
        for (var p : points) {
            cnt.merge(p[1], 1, Integer::sum);
        }
        long ans = 0, s = 0;
        for (int v : cnt.values()) {
            long t = 1L * v * (v - 1) / 2;
            ans = (ans + s * t) % mod;
            s += t;
        }
        return (int) ans;
    }
}

class Solution {
public:
    int countTrapezoids(vector<vector<int>>& points) {
        const int mod = 1e9 + 7;
        unordered_map<int, int> cnt;
        for (auto& p : points) {
            cnt[p[1]]++;
        }
        long long ans = 0, s = 0;
        for (auto& [_, v] : cnt) {
            long long t = 1LL * v * (v - 1) / 2;
            ans = (ans + s * t) % mod;
            s += t;
        }
        return (int) ans;
    }
};

func countTrapezoids(points [][]int) int {
    const mod = 1_000_000_007
    cnt := make(map[int]int)
    for _, p := range points {
        cnt[p[1]]++
    }

    var ans, s int64
    for _, v := range cnt {
        t := int64(v) * int64(v-1) / 2
        ans = (ans + s*t) % mod
        s += t
    }
    return int(ans)
}

function countTrapezoids(points: number[][]): number {
    const mod = 1_000_000_007;
    const cnt = new Map<number, number>();

    for (const p of points) {
        cnt.set(p[1], (cnt.get(p[1]) ?? 0) + 1);
    }

    let ans = 0;
    let s = 0;
    for (const v of cnt.values()) {
        const t = (v * (v - 1)) / 2;
        const mul = BigInt(s) * BigInt(t);
        ans = Number((BigInt(ans) + mul) % BigInt(mod));
        s += t;
    }

    return ans;
}

3623. 统计梯形的数目 I

题目描述

解法

方法一：枚举

评论