


题目描述
给你一个 m x n 的矩阵 grid 和一个正整数 k。一个 岛屿 是由 正 整数(表示陆地)组成的,并且陆地间 四周 连通(水平或垂直)。
一个岛屿的总价值是该岛屿中所有单元格的值之和。
返回总价值可以被 k 整除 的岛屿数量。
示例 1:
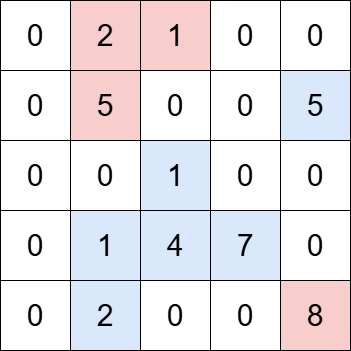
输入: grid = [[0,2,1,0,0],[0,5,0,0,5],[0,0,1,0,0],[0,1,4,7,0],[0,2,0,0,8]], k = 5
输出: 2
解释:
网格中包含四个岛屿。蓝色高亮显示的岛屿的总价值可以被 5 整除,而红色高亮显示的岛屿则不能。
示例 2:
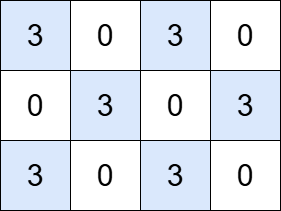
输入: grid = [[3,0,3,0], [0,3,0,3], [3,0,3,0]], k = 3
输出: 6
解释:
网格中包含六个岛屿,每个岛屿的总价值都可以被 3 整除。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 1050 <= grid[i][j] <= 1061 <= k < = 106
解法
方法一:DFS
我们定义一个函数 \(\textit{dfs}(i, j)\),它从位置 \((i, j)\) 开始进行 DFS 遍历,并且返回该岛屿的总价值。我们将当前位置的值加入总价值,然后将该位置标记为已访问(例如,将其值设为 0)。接着,我们递归地访问四个方向(上、下、左、右)的相邻位置,如果相邻位置的值大于 0,则继续进行 DFS,并将其值加入总价值。最后,我们返回总价值。
在主函数中,我们遍历整个网格,对于每个未访问的位置 \((i, j)\),如果其值大于 0,则调用 \(\textit{dfs}(i, j)\) 来计算该岛屿的总价值。如果总价值可以被 \(k\) 整除,则将答案加一。
时间复杂度 \(O(m \times n)\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别是网格的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | class Solution:
def countIslands(self, grid: List[List[int]], k: int) -> int:
def dfs(i: int, j: int) -> int:
s = grid[i][j]
grid[i][j] = 0
for a, b in pairwise(dirs):
x, y = i + a, j + b
if 0 <= x < m and 0 <= y < n and grid[x][y]:
s += dfs(x, y)
return s
m, n = len(grid), len(grid[0])
dirs = (-1, 0, 1, 0, -1)
ans = 0
for i in range(m):
for j in range(n):
if grid[i][j] and dfs(i, j) % k == 0:
ans += 1
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | class Solution {
private int m;
private int n;
private int[][] grid;
private final int[] dirs = {-1, 0, 1, 0, -1};
public int countIslands(int[][] grid, int k) {
m = grid.length;
n = grid[0].length;
this.grid = grid;
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] > 0 && dfs(i, j) % k == 0) {
++ans;
}
}
}
return ans;
}
private long dfs(int i, int j) {
long s = grid[i][j];
grid[i][j] = 0;
for (int d = 0; d < 4; ++d) {
int x = i + dirs[d], y = j + dirs[d + 1];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0) {
s += dfs(x, y);
}
}
return s;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | class Solution {
public:
int countIslands(vector<vector<int>>& grid, int k) {
int m = grid.size(), n = grid[0].size();
vector<int> dirs = {-1, 0, 1, 0, -1};
auto dfs = [&](this auto&& dfs, int i, int j) -> long long {
long long s = grid[i][j];
grid[i][j] = 0;
for (int d = 0; d < 4; ++d) {
int x = i + dirs[d], y = j + dirs[d + 1];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y]) {
s += dfs(x, y);
}
}
return s;
};
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] && dfs(i, j) % k == 0) {
++ans;
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | func countIslands(grid [][]int, k int) (ans int) {
m, n := len(grid), len(grid[0])
dirs := []int{-1, 0, 1, 0, -1}
var dfs func(i, j int) int
dfs = func(i, j int) int {
s := grid[i][j]
grid[i][j] = 0
for d := 0; d < 4; d++ {
x, y := i+dirs[d], j+dirs[d+1]
if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0 {
s += dfs(x, y)
}
}
return s
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if grid[i][j] > 0 && dfs(i, j)%k == 0 {
ans++
}
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | function countIslands(grid: number[][], k: number): number {
const m = grid.length,
n = grid[0].length;
const dirs = [-1, 0, 1, 0, -1];
const dfs = (i: number, j: number): number => {
let s = grid[i][j];
grid[i][j] = 0;
for (let d = 0; d < 4; d++) {
const x = i + dirs[d],
y = j + dirs[d + 1];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0) {
s += dfs(x, y);
}
}
return s;
};
let ans = 0;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] > 0 && dfs(i, j) % k === 0) {
ans++;
}
}
}
return ans;
}
|




