


题目描述
给你一个无向连通图,包含 n 个节点,节点编号从 0 到 n - 1,以及一个二维整数数组 edges,其中 edges[i] = [ui, vi, wi] 表示一条连接节点 ui 和节点 vi 的无向边,边权为 wi,另有一个整数 k。
你可以从图中移除任意数量的边,使得最终的图中 最多 只包含 k 个连通分量。
连通分量的 成本 定义为该分量中边权的 最大值 。如果一个连通分量没有边,则其代价为 0。
请返回在移除这些边之后,在所有连通分量之中的 最大成本 的 最小可能值 。
示例 1:
输入: n = 5, edges = [[0,1,4],[1,2,3],[1,3,2],[3,4,6]], k = 2
输出: 4
解释:
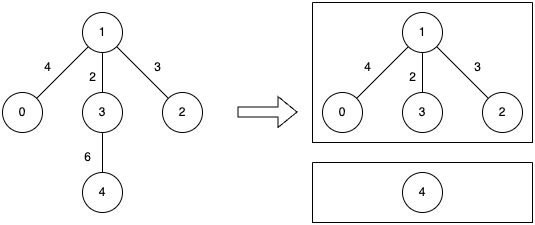
- 移除节点 3 和节点 4 之间的边(权值为 6)。
- 最终的连通分量成本分别为 0 和 4,因此最大代价为 4。
示例 2:
输入: n = 4, edges = [[0,1,5],[1,2,5],[2,3,5]], k = 1
输出: 5
解释:

- 无法移除任何边,因为只允许一个连通分量(
k = 1),图必须保持完全连通。 - 该连通分量的成本等于其最大边权,即 5。
提示:
1 <= n <= 5 * 1040 <= edges.length <= 105edges[i].length == 30 <= ui, vi < n1 <= wi <= 1061 <= k <= n- 输入图是连通图。
解法
方法一:排序 + 并查集
如果 \(k = n\),说明所有的边都可以被移除,此时所有的连通分量都是孤立的节点,最大成本为 0。
否则,我们可以将所有的边按权值从小到大排序,然后使用并查集来维护连通分量。
我们不妨假设初始时所有节点并不联通,初始时每个节点都是一个独立的连通分量。我们从权值最小的边开始,尝试将其加入到当前的连通分量中。如果加入后连通分量的数量已经小于等于 \(k\),则说明剩余的边都可以被移除,此时当前边的权值就是我们要找的最大成本,返回该权值即可。否则,我们继续处理下一条边。
时间复杂度 \(O(n \times \log n)\),空间复杂度 \(O(n)\)。其中 \(n\) 是节点的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution:
def minCost(self, n: int, edges: List[List[int]], k: int) -> int:
def find(x: int) -> int:
if p[x] != x:
p[x] = find(p[x])
return p[x]
if k == n:
return 0
edges.sort(key=lambda x: x[2])
cnt = n
p = list(range(n))
for u, v, w in edges:
pu, pv = find(u), find(v)
if pu != pv:
p[pu] = pv
cnt -= 1
if cnt <= k:
return w
return 0
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | class Solution {
private int[] p;
public int minCost(int n, int[][] edges, int k) {
if (k == n) {
return 0;
}
p = new int[n];
Arrays.setAll(p, i -> i);
Arrays.sort(edges, Comparator.comparingInt(a -> a[2]));
int cnt = n;
for (var e : edges) {
int u = e[0], v = e[1], w = e[2];
int pu = find(u), pv = find(v);
if (pu != pv) {
p[pu] = pv;
if (--cnt <= k) {
return w;
}
}
}
return 0;
}
private int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | class Solution {
public:
int minCost(int n, vector<vector<int>>& edges, int k) {
if (k == n) {
return 0;
}
vector<int> p(n);
ranges::iota(p, 0);
ranges::sort(edges, {}, [](const auto& e) { return e[2]; });
auto find = [&](this auto&& find, int x) -> int {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
};
int cnt = n;
for (const auto& e : edges) {
int u = e[0], v = e[1], w = e[2];
int pu = find(u), pv = find(v);
if (pu != pv) {
p[pu] = pv;
if (--cnt <= k) {
return w;
}
}
}
return 0;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 | func minCost(n int, edges [][]int, k int) int {
p := make([]int, n)
for i := range p {
p[i] = i
}
var find func(int) int
find = func(x int) int {
if p[x] != x {
p[x] = find(p[x])
}
return p[x]
}
if k == n {
return 0
}
slices.SortFunc(edges, func(a, b []int) int {
return a[2] - b[2]
})
cnt := n
for _, e := range edges {
u, v, w := e[0], e[1], e[2]
pu, pv := find(u), find(v)
if pu != pv {
p[pu] = pv
if cnt--; cnt <= k {
return w
}
}
}
return 0
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | function minCost(n: number, edges: number[][], k: number): number {
const p: number[] = Array.from({ length: n }, (_, i) => i);
const find = (x: number): number => {
if (p[x] !== x) {
p[x] = find(p[x]);
}
return p[x];
};
if (k === n) {
return 0;
}
edges.sort((a, b) => a[2] - b[2]);
let cnt = n;
for (const [u, v, w] of edges) {
const pu = find(u),
pv = find(v);
if (pu !== pv) {
p[pu] = pv;
if (--cnt <= k) {
return w;
}
}
}
return 0;
}
|




