
题目描述
给定一个 m x n 大小的 2 维数组 grid,和一个整数 k。grid 中有 k 个单元格包含从 1 到 k 的值,每个值恰好出现一次,其余单元格的值为 0。
你可以从任何单元格开始,并且从一个单元格移动到相邻的单元格(上,下,左,右)。你必须找到一条 grid 中的路径,满足:
- 访问
grid 中的每个单元格 恰好一次。 - 按顺序 访问值为 1 到
k 的单元格。
返回一个大小为 (m * n) 的二维数组 result,其中 result[i] = [xi, yi] 表示路径中访问的第 i 个单元格。如果存在多条这样的路径,你可以返回 任何 一条。
如果不存在这样的路径,返回一个 空 数组。
示例 1:
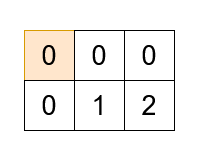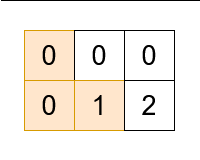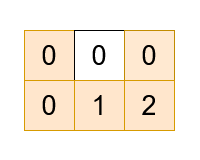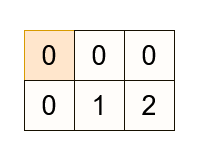
输入:grid = [[0,0,0],[0,1,2]], k = 2
输出:[[0,0],[1,0],[1,1],[1,2],[0,2],[0,1]]
解释:
示例 2:
输入:grid = [[1,0,4],[3,0,2]], k = 4
输出:[]
解释:
没有满足条件的路径。
提示:
1 <= m == grid.length <= 51 <= n == grid[i].length <= 51 <= k <= m * n0 <= grid[i][j] <= kgrid 包含 1 到 k 的所有整数 恰好 一次。
解法
方法一:状态压缩 + DFS
我们注意到,矩阵的大小不超过 \(6 \times 6\),因此可以使用状态压缩来表示已经访问过的格子。我们可以使用一个整数 \(\textit{st}\) 来表示已经访问过的格子,其中第 \(i\) 位为 1 表示格子 \(i\) 已经被访问过,0 表示未被访问过。
接下来,我们遍历每一个格子作为起点,如果该格子是 0 或 1,则从该格子开始进行深度优先搜索(DFS)。在 DFS 中,我们将当前格子加入路径中,并将其标记为已访问。然后,我们检查当前格子的值,如果等于 \(v\),则将 \(v\) 加 1。接着,我们尝试向四个方向移动到相邻的格子,如果相邻格子未被访问且其值为 0 或 \(v\),则继续进行 DFS。
如果 DFS 成功找到了一条完整的路径,则返回该路径。如果无法找到完整路径,则回溯,撤销当前格子的访问标记,并尝试其他方向。
时间复杂度 \(O(m^2 \times n^2)\),空间复杂度 \(O(m \times n)\),其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 | class Solution:
def findPath(self, grid: List[List[int]], k: int) -> List[List[int]]:
def f(i: int, j: int) -> int:
return i * n + j
def dfs(i: int, j: int, v: int):
nonlocal st
path.append([i, j])
if len(path) == m * n:
return True
st |= 1 << f(i, j)
if grid[i][j] == v:
v += 1
for a, b in pairwise(dirs):
x, y = i + a, j + b
if (
0 <= x < m
and 0 <= y < n
and (st & 1 << f(x, y)) == 0
and grid[x][y] in (0, v)
):
if dfs(x, y, v):
return True
path.pop()
st ^= 1 << f(i, j)
return False
m, n = len(grid), len(grid[0])
st = 0
path = []
dirs = (-1, 0, 1, 0, -1)
for i in range(m):
for j in range(n):
if grid[i][j] in (0, 1):
if dfs(i, j, 1):
return path
path.clear()
st = 0
return []
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 | class Solution {
private int m, n;
private long st = 0;
private List<List<Integer>> path = new ArrayList<>();
private final int[] dirs = {-1, 0, 1, 0, -1};
private int f(int i, int j) {
return i * n + j;
}
private boolean dfs(int i, int j, int v, int[][] grid) {
path.add(Arrays.asList(i, j));
if (path.size() == m * n) {
return true;
}
st |= 1L << f(i, j);
if (grid[i][j] == v) {
v += 1;
}
for (int t = 0; t < 4; t++) {
int a = dirs[t], b = dirs[t + 1];
int x = i + a, y = j + b;
if (0 <= x && x < m && 0 <= y && y < n && (st & (1L << f(x, y))) == 0
&& (grid[x][y] == 0 || grid[x][y] == v)) {
if (dfs(x, y, v, grid)) {
return true;
}
}
}
path.remove(path.size() - 1);
st ^= 1L << f(i, j);
return false;
}
public List<List<Integer>> findPath(int[][] grid, int k) {
m = grid.length;
n = grid[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 0 || grid[i][j] == 1) {
if (dfs(i, j, 1, grid)) {
return path;
}
path.clear();
st = 0;
}
}
}
return List.of();
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52 | class Solution {
int m, n;
unsigned long long st = 0;
vector<vector<int>> path;
int dirs[5] = {-1, 0, 1, 0, -1};
int f(int i, int j) {
return i * n + j;
}
bool dfs(int i, int j, int v, vector<vector<int>>& grid) {
path.push_back({i, j});
if (path.size() == static_cast<size_t>(m * n)) {
return true;
}
st |= 1ULL << f(i, j);
if (grid[i][j] == v) {
v += 1;
}
for (int t = 0; t < 4; ++t) {
int a = dirs[t], b = dirs[t + 1];
int x = i + a, y = j + b;
if (0 <= x && x < m && 0 <= y && y < n && (st & (1ULL << f(x, y))) == 0
&& (grid[x][y] == 0 || grid[x][y] == v)) {
if (dfs(x, y, v, grid)) {
return true;
}
}
}
path.pop_back();
st ^= 1ULL << f(i, j);
return false;
}
public:
vector<vector<int>> findPath(vector<vector<int>>& grid, int k) {
m = grid.size();
n = grid[0].size();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0 || grid[i][j] == 1) {
if (dfs(i, j, 1, grid)) {
return path;
}
path.clear();
st = 0;
}
}
}
return {};
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 | func findPath(grid [][]int, k int) [][]int {
_ = k
m := len(grid)
n := len(grid[0])
var st uint64
path := [][]int{}
dirs := []int{-1, 0, 1, 0, -1}
f := func(i, j int) int { return i*n + j }
var dfs func(int, int, int) bool
dfs = func(i, j, v int) bool {
path = append(path, []int{i, j})
if len(path) == m*n {
return true
}
idx := f(i, j)
st |= 1 << idx
if grid[i][j] == v {
v++
}
for t := 0; t < 4; t++ {
a, b := dirs[t], dirs[t+1]
x, y := i+a, j+b
if 0 <= x && x < m && 0 <= y && y < n {
idx2 := f(x, y)
if (st>>idx2)&1 == 0 && (grid[x][y] == 0 || grid[x][y] == v) {
if dfs(x, y, v) {
return true
}
}
}
}
path = path[:len(path)-1]
st ^= 1 << idx
return false
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if grid[i][j] == 0 || grid[i][j] == 1 {
if dfs(i, j, 1) {
return path
}
path = path[:0]
st = 0
}
}
}
return [][]int{}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60 | function findPath(grid: number[][], k: number): number[][] {
const m = grid.length;
const n = grid[0].length;
const dirs = [-1, 0, 1, 0, -1];
const path: number[][] = [];
let st = 0;
function f(i: number, j: number): number {
return i * n + j;
}
function dfs(i: number, j: number, v: number): boolean {
path.push([i, j]);
if (path.length === m * n) {
return true;
}
st |= 1 << f(i, j);
if (grid[i][j] === v) {
v += 1;
}
for (let d = 0; d < 4; d++) {
const x = i + dirs[d];
const y = j + dirs[d + 1];
const pos = f(x, y);
if (
x >= 0 &&
x < m &&
y >= 0 &&
y < n &&
(st & (1 << pos)) === 0 &&
(grid[x][y] === 0 || grid[x][y] === v)
) {
if (dfs(x, y, v)) {
return true;
}
}
}
path.pop();
st ^= 1 << f(i, j);
return false;
}
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] === 0 || grid[i][j] === 1) {
st = 0;
path.length = 0;
if (dfs(i, j, 1)) {
return path;
}
}
}
}
return [];
}
|

