


题目描述
给你一个大小为 m x n 的二维字符网格 matrix,用字符串数组表示,其中 matrix[i][j] 表示第 i 行和第 j 列处的单元格。每个单元格可以是以下几种字符之一:
'.' 表示一个空单元格。'#' 表示一个障碍物。- 一个大写字母(
'A' 到 'Z')表示一个传送门。
你从左上角单元格 (0, 0) 出发,目标是到达右下角单元格 (m - 1, n - 1)。你可以从当前位置移动到相邻的单元格(上、下、左、右),移动后的单元格必须在网格边界内且不是障碍物。
如果你踏入一个包含传送门字母的单元格,并且你之前没有使用过该传送门字母,你可以立即传送到网格中另一个具有相同字母的单元格。这次传送不计入移动次数,但每个字母对应的传送门在旅程中 最多 只能使用一次。
返回到达右下角单元格所需的 最少 移动次数。如果无法到达目的地,则返回 -1。
示例 1:
输入: matrix = ["A..",".A.","..."]
输出: 2
解释:
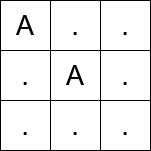
- 在第一次移动之前,从
(0, 0) 传送到 (1, 1)。 - 第一次移动,从
(1, 1) 移动到 (1, 2)。 - 第二次移动,从
(1, 2) 移动到 (2, 2)。
示例 2:
输入: matrix = [".#...",".#.#.",".#.#.","...#."]
输出: 13
解释:
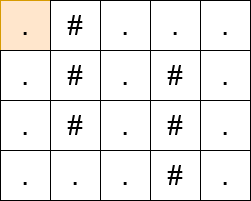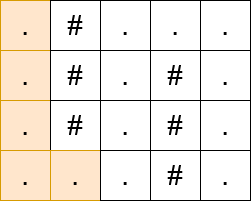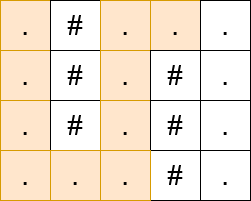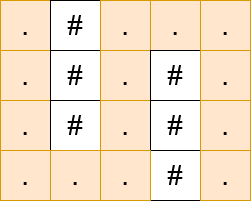
提示:
1 <= m == matrix.length <= 1031 <= n == matrix[i].length <= 103matrix[i][j] 是 '#'、'.' 或一个大写英文字母。matrix[0][0] 不是障碍物。
解法
方法一:0-1 BFS
我们可以使用 0-1 BFS 来解决这个问题。我们从左上角单元格开始,使用双端队列来存储当前单元格的坐标。每次从队列中取出一个单元格,我们会检查它的四个相邻单元格,如果相邻单元格是空单元格且没有被访问过,我们就将它加入队列,并更新它的距离。
如果相邻单元格是一个传送门,我们就将它加入队列的前面,并更新它的距离。我们还需要维护一个字典来存储每个传送门的位置,以便在使用传送门时能够快速找到它们。
我们还需要一个二维数组来存储每个单元格的距离,初始值为无穷大。我们将起点的距离设置为 0,然后开始 BFS。
在 BFS 的过程中,我们会检查每个单元格是否是终点,如果是,就返回它的距离。如果队列为空,说明无法到达终点,返回 -1。
时间复杂度 \(O(m \times n)\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | class Solution:
def minMoves(self, matrix: List[str]) -> int:
m, n = len(matrix), len(matrix[0])
g = defaultdict(list)
for i, row in enumerate(matrix):
for j, c in enumerate(row):
if c.isalpha():
g[c].append((i, j))
dirs = (-1, 0, 1, 0, -1)
dist = [[inf] * n for _ in range(m)]
dist[0][0] = 0
q = deque([(0, 0)])
while q:
i, j = q.popleft()
d = dist[i][j]
if i == m - 1 and j == n - 1:
return d
c = matrix[i][j]
if c in g:
for x, y in g[c]:
if d < dist[x][y]:
dist[x][y] = d
q.appendleft((x, y))
del g[c]
for a, b in pairwise(dirs):
x, y = i + a, j + b
if (
0 <= x < m
and 0 <= y < n
and matrix[x][y] != "#"
and d + 1 < dist[x][y]
):
dist[x][y] = d + 1
q.append((x, y))
return -1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49 | class Solution {
public int minMoves(String[] matrix) {
int m = matrix.length, n = matrix[0].length();
Map<Character, List<int[]>> g = new HashMap<>();
for (int i = 0; i < m; i++) {
String row = matrix[i];
for (int j = 0; j < n; j++) {
char c = row.charAt(j);
if (Character.isAlphabetic(c)) {
g.computeIfAbsent(c, k -> new ArrayList<>()).add(new int[] {i, j});
}
}
}
int[] dirs = {-1, 0, 1, 0, -1};
int INF = Integer.MAX_VALUE / 2;
int[][] dist = new int[m][n];
for (int[] arr : dist) Arrays.fill(arr, INF);
dist[0][0] = 0;
Deque<int[]> q = new ArrayDeque<>();
q.add(new int[] {0, 0});
while (!q.isEmpty()) {
int[] cur = q.pollFirst();
int i = cur[0], j = cur[1];
int d = dist[i][j];
if (i == m - 1 && j == n - 1) return d;
char c = matrix[i].charAt(j);
if (g.containsKey(c)) {
for (int[] pos : g.get(c)) {
int x = pos[0], y = pos[1];
if (d < dist[x][y]) {
dist[x][y] = d;
q.addFirst(new int[] {x, y});
}
}
g.remove(c);
}
for (int idx = 0; idx < 4; idx++) {
int a = dirs[idx], b = dirs[idx + 1];
int x = i + a, y = j + b;
if (0 <= x && x < m && 0 <= y && y < n && matrix[x].charAt(y) != '#'
&& d + 1 < dist[x][y]) {
dist[x][y] = d + 1;
q.addLast(new int[] {x, y});
}
}
}
return -1;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | class Solution {
public:
int minMoves(vector<string>& matrix) {
int m = matrix.size(), n = matrix[0].size();
unordered_map<char, vector<pair<int, int>>> g;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j) {
char c = matrix[i][j];
if (isalpha(c)) g[c].push_back({i, j});
}
int dirs[5] = {-1, 0, 1, 0, -1};
int INF = numeric_limits<int>::max() / 2;
vector<vector<int>> dist(m, vector<int>(n, INF));
dist[0][0] = 0;
deque<pair<int, int>> q;
q.push_back({0, 0});
while (!q.empty()) {
auto [i, j] = q.front();
q.pop_front();
int d = dist[i][j];
if (i == m - 1 && j == n - 1) return d;
char c = matrix[i][j];
if (g.count(c)) {
for (auto [x, y] : g[c])
if (d < dist[x][y]) {
dist[x][y] = d;
q.push_front({x, y});
}
g.erase(c);
}
for (int idx = 0; idx < 4; ++idx) {
int x = i + dirs[idx], y = j + dirs[idx + 1];
if (0 <= x && x < m && 0 <= y && y < n && matrix[x][y] != '#' && d + 1 < dist[x][y]) {
dist[x][y] = d + 1;
q.push_back({x, y});
}
}
}
return -1;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52 | type pair struct{ x, y int }
func minMoves(matrix []string) int {
m, n := len(matrix), len(matrix[0])
g := make(map[rune][]pair)
for i := 0; i < m; i++ {
for j, c := range matrix[i] {
if unicode.IsLetter(c) {
g[c] = append(g[c], pair{i, j})
}
}
}
dirs := []int{-1, 0, 1, 0, -1}
INF := 1 << 30
dist := make([][]int, m)
for i := range dist {
dist[i] = make([]int, n)
for j := range dist[i] {
dist[i][j] = INF
}
}
dist[0][0] = 0
q := list.New()
q.PushBack(pair{0, 0})
for q.Len() > 0 {
cur := q.Remove(q.Front()).(pair)
i, j := cur.x, cur.y
d := dist[i][j]
if i == m-1 && j == n-1 {
return d
}
c := rune(matrix[i][j])
if v, ok := g[c]; ok {
for _, p := range v {
x, y := p.x, p.y
if d < dist[x][y] {
dist[x][y] = d
q.PushFront(pair{x, y})
}
}
delete(g, c)
}
for idx := 0; idx < 4; idx++ {
x, y := i+dirs[idx], j+dirs[idx+1]
if 0 <= x && x < m && 0 <= y && y < n && matrix[x][y] != '#' && d+1 < dist[x][y] {
dist[x][y] = d + 1
q.PushBack(pair{x, y})
}
}
}
return -1
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61 | function minMoves(matrix: string[]): number {
const m = matrix.length,
n = matrix[0].length;
const g = new Map<string, [number, number][]>();
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
const c = matrix[i][j];
if (/^[A-Za-z]$/.test(c)) {
if (!g.has(c)) g.set(c, []);
g.get(c)!.push([i, j]);
}
}
}
const dirs = [-1, 0, 1, 0, -1];
const INF = Number.MAX_SAFE_INTEGER;
const dist: number[][] = Array.from({ length: m }, () => Array(n).fill(INF));
dist[0][0] = 0;
const cap = m * n * 2 + 5;
const dq = new Array<[number, number]>(cap);
let l = cap >> 1,
r = cap >> 1;
const pushFront = (v: [number, number]) => {
dq[--l] = v;
};
const pushBack = (v: [number, number]) => {
dq[r++] = v;
};
const popFront = (): [number, number] => dq[l++];
const empty = () => l === r;
pushBack([0, 0]);
while (!empty()) {
const [i, j] = popFront();
const d = dist[i][j];
if (i === m - 1 && j === n - 1) return d;
const c = matrix[i][j];
if (g.has(c)) {
for (const [x, y] of g.get(c)!) {
if (d < dist[x][y]) {
dist[x][y] = d;
pushFront([x, y]);
}
}
g.delete(c);
}
for (let idx = 0; idx < 4; idx++) {
const x = i + dirs[idx],
y = j + dirs[idx + 1];
if (0 <= x && x < m && 0 <= y && y < n && matrix[x][y] !== '#' && d + 1 < dist[x][y]) {
dist[x][y] = d + 1;
pushBack([x, y]);
}
}
}
return -1;
}
|




