3537. 填充特殊网格

题目描述

给你一个非负整数 N，表示一个 2N x 2N 的网格。你需要用从 0 到 22N - 1 的整数填充网格，使其成为一个 特殊 网格。一个网格当且仅当满足以下 所有 条件时，才能称之为 特殊 网格：

• 右上角象限中的所有数字都小于右下角象限中的所有数字。
• 右下角象限中的所有数字都小于左下角象限中的所有数字。
• 左下角象限中的所有数字都小于左上角象限中的所有数字。
• 每个象限也都是一个特殊网格。

返回一个 2N x 2N 的特殊网格。

注意：任何 1x1 的网格都是特殊网格。

 

示例 1：

输入： N = 0

输出： [[0]]

解释：

唯一可以放置的数字是 0，并且网格中只有一个位置。

示例 2：

输入： N = 1

输出： [[3,0],[2,1]]

解释：

每个象限的数字如下：

• 右上角：0
• 右下角：1
• 左下角：2
• 左上角：3

由于 0 < 1 < 2 < 3，该网格满足给定的约束条件。

示例 3：

输入： N = 2

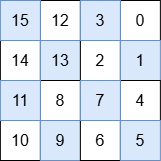
输出： [[15,12,3,0],[14,13,2,1],[11,8,7,4],[10,9,6,5]]

解释：

每个象限的数字如下：

• 右上角：3, 0, 2, 1
• 右下角：7, 4, 6, 5
• 左下角：11, 8, 10, 9
• 左上角：15, 12, 14, 13
• max(3, 0, 2, 1) < min(7, 4, 6, 5)
• max(7, 4, 6, 5) < min(11, 8, 10, 9)
• max(11, 8, 10, 9) < min(15, 12, 14, 13)

这满足前三个要求。此外，每个象限也是一个特殊网格。因此，这是一个特殊网格。

 

提示：

• 0 <= N <= 10

解法

方法一

Python3JavaC++Go

评论