3534. 针对图的路径存在性查询 II
题目描述
给你一个整数 n,表示图中的节点数量,这些节点按从 0 到 n - 1 编号。
同时给你一个长度为 n 的整数数组 nums,以及一个整数 maxDiff。
如果满足 |nums[i] - nums[j]| <= maxDiff(即 nums[i] 和 nums[j] 的 绝对差 至多为 maxDiff),则节点 i 和节点 j 之间存在一条 无向边 。
此外,给你一个二维整数数组 queries。对于每个 queries[i] = [ui, vi],找到节点 ui 和节点 vi 之间的 最短距离 。如果两节点之间不存在路径,则返回 -1。
返回一个数组 answer,其中 answer[i] 是第 i 个查询的结果。
注意:节点之间的边是无权重(unweighted)的。
示例 1:
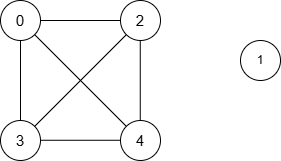
输入: n = 5, nums = [1,8,3,4,2], maxDiff = 3, queries = [[0,3],[2,4]]
输出: [1,1]
解释:
生成的图如下:
| 查询 | 最短路径 | 最短距离 |
|---|---|---|
| [0, 3] | 0 → 3 | 1 |
| [2, 4] | 2 → 4 | 1 |
因此,输出为 [1, 1]。
示例 2:
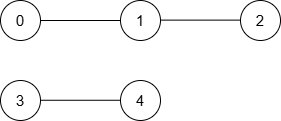
输入: n = 5, nums = [5,3,1,9,10], maxDiff = 2, queries = [[0,1],[0,2],[2,3],[4,3]]
输出: [1,2,-1,1]
解释:
生成的图如下:
| 查询 | 最短路径 | 最短距离 |
|---|---|---|
| [0, 1] | 0 → 1 | 1 |
| [0, 2] | 0 → 1 → 2 | 2 |
| [2, 3] | 无 | -1 |
| [4, 3] | 3 → 4 | 1 |
因此,输出为 [1, 2, -1, 1]。
示例 3:
输入: n = 3, nums = [3,6,1], maxDiff = 1, queries = [[0,0],[0,1],[1,2]]
输出: [0,-1,-1]
解释:
由于以下原因,任意两个节点之间都不存在边:
- 节点 0 和节点 1:
|nums[0] - nums[1]| = |3 - 6| = 3 > 1 - 节点 0 和节点 2:
|nums[0] - nums[2]| = |3 - 1| = 2 > 1 - 节点 1 和节点 2:
|nums[1] - nums[2]| = |6 - 1| = 5 > 1
因此,不存在任何可以到达其他节点的节点,输出为 [0, -1, -1]。
提示:
1 <= n == nums.length <= 1050 <= nums[i] <= 1050 <= maxDiff <= 1051 <= queries.length <= 105queries[i] == [ui, vi]0 <= ui, vi < n
解法
方法一
1 | |
1 | |
1 | |
1 | |