3530. 有向无环图中合法拓扑排序的最大利润

题目描述

给你一个由 n 个节点组成的有向无环图（DAG），节点编号从 0 到 n - 1，通过二维数组 edges 表示，其中 edges[i] = [ui, vi] 表示一条从节点 ui 指向节点 vi 的有向边。每个节点都有一个对应的 得分 ，由数组 score 给出，其中 score[i] 表示节点 i 的得分。

你需要以 有效的拓扑排序 顺序处理这些节点。每个节点在处理顺序中被分配一个编号从 1 开始的位置。

将每个节点的得分乘以其在拓扑排序中的位置，然后求和，得到的值称为 利润。

请返回在所有合法拓扑排序中可获得的 最大利润 。

拓扑排序 是一个对 DAG 中所有节点的线性排序，使得每条有向边 u → v 中，节点 u 都出现在 v 之前。

 

示例 1：

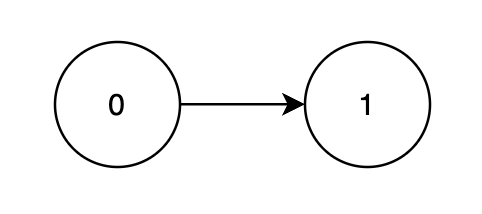
输入： n = 2, edges = [[0,1]], score = [2,3]

输出： 8

解释：

节点 1 依赖于节点 0，因此一个合法顺序是 [0, 1]。

节点	处理顺序	得分	乘数	利润计算
0	第 1 个	2	1	2 × 1 = 2
1	第 2 个	3	2	3 × 2 = 6

所有合法拓扑排序中可获得的最大总利润是 2 + 6 = 8。

示例 2：

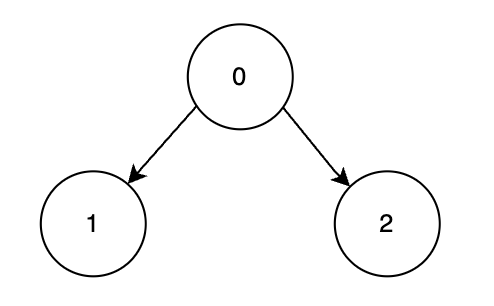
输入： n = 3, edges = [[0,1],[0,2]], score = [1,6,3]

输出： 25

解释：

节点 1 和 2 都依赖于节点 0，因此最优的合法顺序是 [0, 2, 1]。

节点	处理顺序	得分	乘数	利润计算
0	第 1 个	1	1	1 × 1 = 1
2	第 2 个	3	2	3 × 2 = 6
1	第 3 个	6	3	6 × 3 = 18

所有合法拓扑排序中可获得的最大总利润是 1 + 6 + 18 = 25。

 

提示：

• 1 <= n == score.length <= 22
• 1 <= score[i] <= 105
• 0 <= edges.length <= n * (n - 1) / 2
• edges[i] == [ui, vi] 表示一条从 ui 到 vi 的有向边。
• 0 <= ui, vi < n
• ui != vi
• 输入图 保证 是一个 DAG。
• 不存在重复的边。

解法

方法一

Python3JavaC++Go

评论