来源第 155 场双周赛 Q2难度中等分数1579
题目描述
有 n 种单位，编号从 0 到 n - 1。给你一个二维整数数组 conversions，长度为 n - 1，其中 conversions[i] = [sourceUniti, targetUniti, conversionFactori] ，表示一个 sourceUniti 类型的单位等于 conversionFactori 个 targetUniti 类型的单位。
请你返回一个长度为 n 的数组 baseUnitConversion，其中 baseUnitConversion[i] 表示 一个 0 类型单位等于多少个 i 类型单位。由于结果可能很大，请返回每个 baseUnitConversion[i] 对 109 + 7 取模后的值。
示例 1：
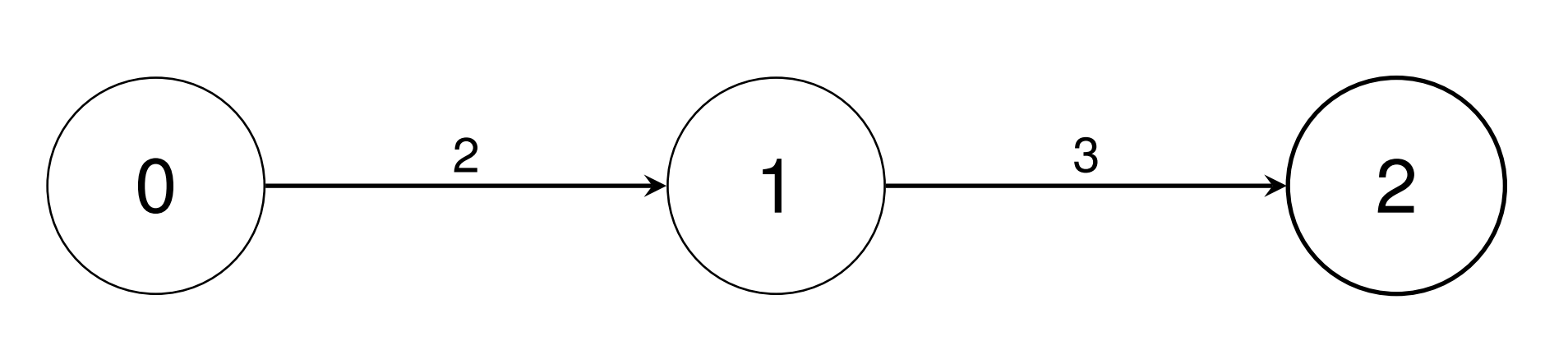
输入： conversions = [[0,1,2],[1,2,3]]
输出： [1,2,6]
解释：
- 使用
conversions[0]：将一个 0 类型单位转换为 2 个 1 类型单位。 - 使用
conversions[0] 和 conversions[1] 将一个 0 类型单位转换为 6 个 2 类型单位。
示例 2：
输入： conversions = [[0,1,2],[0,2,3],[1,3,4],[1,4,5],[2,5,2],[4,6,3],[5,7,4]]
输出： [1,2,3,8,10,6,30,24]
解释：
- 使用
conversions[0] 将一个 0 类型单位转换为 2 个 1 类型单位。 - 使用
conversions[1] 将一个 0 类型单位转换为 3 个 2 类型单位。 - 使用
conversions[0] 和 conversions[2] 将一个 0 类型单位转换为 8 个 3 类型单位。 - 使用
conversions[0] 和 conversions[3] 将一个 0 类型单位转换为 10 个 4 类型单位。 - 使用
conversions[1] 和 conversions[4] 将一个 0 类型单位转换为 6 个 5 类型单位。 - 使用
conversions[0]、conversions[3] 和 conversions[5] 将一个 0 类型单位转换为 30 个 6 类型单位。 - 使用
conversions[1]、conversions[4] 和 conversions[6] 将一个 0 类型单位转换为 24 个 7 类型单位。
提示：
2 <= n <= 105conversions.length == n - 10 <= sourceUniti, targetUniti < n1 <= conversionFactori <= 109- 保证单位 0 可以通过 唯一 的转换路径（不需要反向转换）转换为任何其他单位。
解法
方法一：DFS
思考
转换关系有 \(n-1\) 条且从 \(0\) 可达唯一路径，故为一棵以 \(0\) 为根的有向树。所求为 \(1\) 个单位 \(0\) 等于多少个单位 \(i\)。
邻接表存倍乘因子，从根 DFS 累乘并对 \(10^9+7\) 取模，即可写下 \(\textit{ans}[i]\)。
由于题目保证了单位 0 可以通过唯一的转换路径转换为其他单位，因此我们可以使用深度优先搜索（DFS）来遍历所有单位的转换关系。另外，由于 \(\textit{conversions}\) 数组的长度为 \(n - 1\)，表示有 \(n - 1\) 条转换关系，因此我们可以将单位转换关系看作一棵树，根节点为单位 0，其他节点为其他单位。
我们可以用一个邻接表 \(g\) 来表示单位转换关系，其中 \(g[i]\) 表示单位 \(i\) 可以转换到的单位和对应的转换因子。
然后，我们从根节点 \(0\) 开始进行深度优先搜索，即调函数 \(\textit{dfs}(s, \textit{mul})\)，其中 \(s\) 表示当前单位， \(\textit{mul}\) 表示从单位 \(0\) 转换到单位 \(s\) 的转换因子。初始时 \(s = 0\), \(\textit{mul} = 1\)。在每次递归中，我们将当前单位 \(s\) 的转换因子 \(\textit{mul}\) 存储到答案数组中，然后遍历当前单位 \(s\) 的所有邻接单位 \(t\)，递归调用 \(\textit{dfs}(t, \textit{mul} \times w \mod (10^9 + 7))\)，其中 \(w\) 为单位 \(s\) 转换到单位 \(t\) 的转换因子。
最后，我们返回答案数组即可。
时间复杂度 \(O(n)\)，空间复杂度 \(O(n)\)。其中 \(n\) 为单位的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | class Solution:
def baseUnitConversions(self, conversions: List[List[int]]) -> List[int]:
def dfs(s: int, mul: int) -> None:
ans[s] = mul
for t, w in g[s]:
dfs(t, mul * w % mod)
mod = 10**9 + 7
n = len(conversions) + 1
g = [[] for _ in range(n)]
for s, t, w in conversions:
g[s].append((t, w))
ans = [0] * n
dfs(0, 1)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | class Solution {
private final int mod = (int) 1e9 + 7;
private List<int[]>[] g;
private int[] ans;
private int n;
public int[] baseUnitConversions(int[][] conversions) {
n = conversions.length + 1;
g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
ans = new int[n];
for (var e : conversions) {
g[e[0]].add(new int[] {e[1], e[2]});
}
dfs(0, 1);
return ans;
}
private void dfs(int s, long mul) {
ans[s] = (int) mul;
for (var e : g[s]) {
dfs(e[0], mul * e[1] % mod);
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution {
public:
vector<int> baseUnitConversions(vector<vector<int>>& conversions) {
const int mod = 1e9 + 7;
int n = conversions.size() + 1;
vector<vector<pair<int, int>>> g(n);
vector<int> ans(n);
for (const auto& e : conversions) {
g[e[0]].push_back({e[1], e[2]});
}
auto dfs = [&](this auto&& dfs, int s, long long mul) -> void {
ans[s] = mul;
for (auto [t, w] : g[s]) {
dfs(t, mul * w % mod);
}
};
dfs(0, 1);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | func baseUnitConversions(conversions [][]int) []int {
const mod = int(1e9 + 7)
n := len(conversions) + 1
g := make([][]struct{ t, w int }, n)
for _, e := range conversions {
s, t, w := e[0], e[1], e[2]
g[s] = append(g[s], struct{ t, w int }{t, w})
}
ans := make([]int, n)
var dfs func(s int, mul int)
dfs = func(s int, mul int) {
ans[s] = mul
for _, e := range g[s] {
dfs(e.t, mul*e.w%mod)
}
}
dfs(0, 1)
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | function baseUnitConversions(conversions: number[][]): number[] {
const mod = BigInt(1e9 + 7);
const n = conversions.length + 1;
const g: { t: number; w: number }[][] = Array.from({ length: n }, () => []);
for (const [s, t, w] of conversions) {
g[s].push({ t, w });
}
const ans: number[] = Array(n).fill(0);
const dfs = (s: number, mul: number) => {
ans[s] = mul;
for (const { t, w } of g[s]) {
dfs(t, Number((BigInt(mul) * BigInt(w)) % mod));
}
};
dfs(0, 1);
return ans;
}
|
方法二：显式栈
思考
转换关系有 \(n - 1\) 条且从 \(0\) 可达唯一路径，故为一棵以 \(0\) 为根的有向树。所求为 \(1\) 个单位 \(0\) 等于多少个单位 \(i\)，答案对 \(10^9 + 7\) 取模。
\(n \le 10^5\)。从根递归进入下一单位，链上的调用深度就是 \(n\)，会超出递归栈。每个单位的因子只取决于根到它的唯一路径，与兄弟的访问顺序无关。
因此用显式栈保存 \((单位, 累计因子)\)。弹出时写下答案，再把每个后继以当前因子乘上边权、对模数取余后压入。根的因子是 \(1\)。
由于题目保证了单位 0 可以通过唯一的转换路径转换为其他单位，另外 \(\textit{conversions}\) 的长度为 \(n - 1\)，因此单位转换关系是一棵以 \(0\) 为根的有向树。
我们可以用一个邻接表 \(g\) 来表示单位转换关系，其中 \(g[i]\) 表示单位 \(i\) 可以转换到的单位和对应的转换因子。
然后用显式栈从根出发。栈帧是 \((单位, 累计因子)\)，初始为 \((0, 1)\)。弹出时把累计因子写入答案，再对每个后继单位 \(t\) 和边权 \(w\)，把 \((t, \textit{mul} \times w \bmod (10^9 + 7))\) 压入栈。
最后，我们返回答案数组即可。
时间复杂度 \(O(n)\)，空间复杂度 \(O(n)\)。其中 \(n\) 为单位的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | class Solution:
def baseUnitConversions(self, conversions: List[List[int]]) -> List[int]:
mod = 10**9 + 7
n = len(conversions) + 1
g = [[] for _ in range(n)]
for s, t, w in conversions:
g[s].append((t, w))
ans = [0] * n
stk = [(0, 1)]
while stk:
s, mul = stk.pop()
ans[s] = mul
for t, w in g[s]:
stk.append((t, mul * w % mod))
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | class Solution {
public int[] baseUnitConversions(int[][] conversions) {
final int mod = (int) 1e9 + 7;
int n = conversions.length + 1;
List<int[]>[] g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (var e : conversions) {
g[e[0]].add(new int[] {e[1], e[2]});
}
int[] ans = new int[n];
Deque<long[]> stk = new ArrayDeque<>();
stk.push(new long[] {0, 1});
while (!stk.isEmpty()) {
long[] cur = stk.pop();
int s = (int) cur[0];
long mul = cur[1];
ans[s] = (int) mul;
for (var e : g[s]) {
stk.push(new long[] {e[0], mul * e[1] % mod});
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | class Solution {
public:
vector<int> baseUnitConversions(vector<vector<int>>& conversions) {
const int mod = 1e9 + 7;
int n = conversions.size() + 1;
vector<vector<pair<int, int>>> g(n);
vector<int> ans(n);
for (const auto& e : conversions) {
g[e[0]].push_back({e[1], e[2]});
}
vector<pair<int, long long>> stk{{0, 1}};
while (!stk.empty()) {
auto [s, mul] = stk.back();
stk.pop_back();
ans[s] = mul;
for (auto [t, w] : g[s]) {
stk.push_back({t, mul * w % mod});
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | func baseUnitConversions(conversions [][]int) []int {
const mod = int(1e9 + 7)
n := len(conversions) + 1
g := make([][]struct{ t, w int }, n)
for _, e := range conversions {
s, t, w := e[0], e[1], e[2]
g[s] = append(g[s], struct{ t, w int }{t, w})
}
ans := make([]int, n)
stk := [][2]int{{0, 1}}
for len(stk) > 0 {
cur := stk[len(stk)-1]
stk = stk[:len(stk)-1]
s, mul := cur[0], cur[1]
ans[s] = mul
for _, e := range g[s] {
stk = append(stk, [2]int{e.t, mul * e.w % mod})
}
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | function baseUnitConversions(conversions: number[][]): number[] {
const mod = BigInt(1e9 + 7);
const n = conversions.length + 1;
const g: { t: number; w: number }[][] = Array.from({ length: n }, () => []);
for (const [s, t, w] of conversions) {
g[s].push({ t, w });
}
const ans: number[] = Array(n).fill(0);
const stk: [number, number][] = [[0, 1]];
while (stk.length) {
const [s, mul] = stk.pop()!;
ans[s] = mul;
for (const { t, w } of g[s]) {
stk.push([t, Number((BigInt(mul) * BigInt(w)) % mod)]);
}
}
return ans;
}
|