跳转至

3454. 分割正方形 II

题目描述

给你一个二维整数数组 squares ，其中 squares[i] = [xi, yi, li] 表示一个与 x 轴平行的正方形的左下角坐标和正方形的边长。

找到一个最小的 y 坐标，它对应一条水平线，该线需要满足它以上正方形的总面积 等于 该线以下正方形的总面积。

答案如果与实际答案的误差在 10-5 以内，将视为正确答案。

注意：正方形 可能会 重叠。重叠区域只 统计一次 。

 

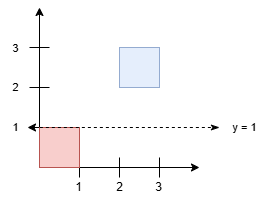
示例 1：

输入： squares = [[0,0,1],[2,2,1]]

输出： 1.00000

解释：

任何在 y = 1 和 y = 2 之间的水平线都会有 1 平方单位的面积在其上方，1 平方单位的面积在其下方。最小的 y 坐标是 1。

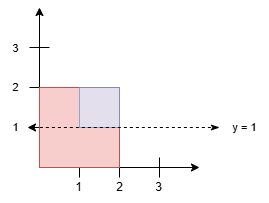
示例 2：

输入： squares = [[0,0,2],[1,1,1]]

输出： 1.00000

解释：

由于蓝色正方形和红色正方形有重叠区域且重叠区域只统计一次。所以直线 y = 1 将正方形分割成两部分且面积相等。

 

提示：

  • 1 <= squares.length <= 5 * 104
  • squares[i] = [xi, yi, li]
  • squares[i].length == 3
  • 0 <= xi, yi <= 109
  • 1 <= li <= 109
  • 所有正方形的总面积不超过 1015。

解法

方法一：扫描线

本题可以使用扫描线算法来计算所有正方形的总面积。

我们将每个正方形的上下边界作为扫描线的事件点，按 \(y\) 坐标从小到大排序。对于每个事件点，我们使用线段树来维护当前扫描线下方被覆盖的 \(x\) 轴区间长度，从而计算出当前扫描线与上一个扫描线之间的面积增量。

具体步骤如下：

  1. 预处理事件点：对于每个正方形，计算其上下边界的 \(y\) 坐标，并将其作为事件点加入事件列表中。每个事件点包含 \(y\) 坐标、左边界 \(x_1\)、右边界 \(x_2\) 以及一个标志（表示是上边界还是下边界）。
  2. 排序事件点：将所有事件点按 \(y\) 坐标从小到大排序。
  3. 构建线段树：使用离散化后的 \(x\) 坐标构建线段树，用于维护当前被覆盖的 \(x\) 轴区间长度。
  4. 扫描事件点：遍历排序后的事件点列表，对于每个事件点：
    • 计算当前事件点与上一个事件点之间的面积增量，并累加到总面积中。
    • 根据当前事件点的类型（上边界或下边界），更新线段树，增加或减少对应的 \(x\) 轴区间覆盖计数。
  5. 计算目标面积：总面积的一半即为目标面积。
  6. 再次扫描事件点：再次遍历事件点列表，计算累计面积，当累计面积达到目标面积时，计算并返回对应的 \(y\) 坐标。

时间复杂度 \(O(n \times \log n)\)，空间复杂度 \(O(n)\)。其中 \(n\) 是正方形的数量。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
class Node:
    __slots__ = ("l", "r", "cnt", "length")

    def __init__(self):
        self.l = self.r = 0
        self.cnt = self.length = 0


class SegmentTree:
    def __init__(self, nums):
        n = len(nums) - 1
        self.nums = nums
        self.tr = [Node() for _ in range(n << 2)]
        self.build(1, 0, n - 1)

    def build(self, u, l, r):
        self.tr[u].l, self.tr[u].r = l, r
        if l != r:
            mid = (l + r) >> 1
            self.build(u << 1, l, mid)
            self.build(u << 1 | 1, mid + 1, r)

    def modify(self, u, l, r, k):
        if self.tr[u].l >= l and self.tr[u].r <= r:
            self.tr[u].cnt += k
        else:
            mid = (self.tr[u].l + self.tr[u].r) >> 1
            if l <= mid:
                self.modify(u << 1, l, r, k)
            if r > mid:
                self.modify(u << 1 | 1, l, r, k)
        self.pushup(u)

    def pushup(self, u):
        if self.tr[u].cnt:
            self.tr[u].length = self.nums[self.tr[u].r + 1] - self.nums[self.tr[u].l]
        elif self.tr[u].l == self.tr[u].r:
            self.tr[u].length = 0
        else:
            self.tr[u].length = self.tr[u << 1].length + self.tr[u << 1 | 1].length

    @property
    def length(self):
        return self.tr[1].length


class Solution:
    def separateSquares(self, squares: List[List[int]]) -> float:
        xs = set()
        segs = []
        for x1, y1, l in squares:
            x2, y2 = x1 + l, y1 + l
            xs.update([x1, x2])
            segs.append((y1, x1, x2, 1))
            segs.append((y2, x1, x2, -1))
        segs.sort()
        st = sorted(xs)
        tree = SegmentTree(st)
        d = {x: i for i, x in enumerate(st)}
        area = 0
        y0 = 0
        for y, x1, x2, k in segs:
            area += (y - y0) * tree.length
            tree.modify(1, d[x1], d[x2] - 1, k)
            y0 = y

        target = area / 2
        area = 0
        y0 = 0
        for y, x1, x2, k in segs:
            t = (y - y0) * tree.length
            if area + t >= target:
                return y0 + (target - area) / tree.length
            area += t
            tree.modify(1, d[x1], d[x2] - 1, k)
            y0 = y
        return 0

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
class Node {
    int l, r, cnt, length;
}

class SegmentTree {
    private Node[] tr;
    private int[] nums;

    public SegmentTree(int[] nums) {
        this.nums = nums;
        int n = nums.length - 1;
        tr = new Node[n << 2];
        for (int i = 0; i < tr.length; ++i) {
            tr[i] = new Node();
        }
        build(1, 0, n - 1);
    }

    private void build(int u, int l, int r) {
        tr[u].l = l;
        tr[u].r = r;
        if (l != r) {
            int mid = (l + r) >> 1;
            build(u << 1, l, mid);
            build(u << 1 | 1, mid + 1, r);
        }
    }

    public void modify(int u, int l, int r, int k) {
        if (tr[u].l >= l && tr[u].r <= r) {
            tr[u].cnt += k;
        } else {
            int mid = (tr[u].l + tr[u].r) >> 1;
            if (l <= mid) {
                modify(u << 1, l, r, k);
            }
            if (r > mid) {
                modify(u << 1 | 1, l, r, k);
            }
        }
        pushup(u);
    }

    private void pushup(int u) {
        if (tr[u].cnt > 0) {
            tr[u].length = nums[tr[u].r + 1] - nums[tr[u].l];
        } else if (tr[u].l == tr[u].r) {
            tr[u].length = 0;
        } else {
            tr[u].length = tr[u << 1].length + tr[u << 1 | 1].length;
        }
    }

    public int query() {
        return tr[1].length;
    }
}

class Solution {
    public double separateSquares(int[][] squares) {
        Set<Integer> xs = new HashSet<>();
        List<int[]> segs = new ArrayList<>();
        for (int[] sq : squares) {
            int x1 = sq[0], y1 = sq[1], l = sq[2];
            int x2 = x1 + l, y2 = y1 + l;
            xs.add(x1);
            xs.add(x2);
            segs.add(new int[] {y1, x1, x2, 1});
            segs.add(new int[] {y2, x1, x2, -1});
        }
        segs.sort(Comparator.comparingInt(a -> a[0]));
        int[] st = new int[xs.size()];
        int i = 0;
        for (int x : xs) {
            st[i++] = x;
        }
        Arrays.sort(st);
        SegmentTree tree = new SegmentTree(st);
        Map<Integer, Integer> d = new HashMap<>(st.length);
        for (i = 0; i < st.length; i++) {
            d.put(st[i], i);
        }
        double area = 0.0;
        int y0 = 0;
        for (int[] s : segs) {
            int y = s[0], x1 = s[1], x2 = s[2], k = s[3];
            area += (double) (y - y0) * tree.query();
            tree.modify(1, d.get(x1), d.get(x2) - 1, k);
            y0 = y;
        }
        double target = area / 2.0;
        area = 0.0;
        y0 = 0;
        for (int[] s : segs) {
            int y = s[0], x1 = s[1], x2 = s[2], k = s[3];
            double t = (double) (y - y0) * tree.query();
            if (area + t >= target) {
                return y0 + (target - area) / tree.query();
            }
            area += t;
            tree.modify(1, d.get(x1), d.get(x2) - 1, k);
            y0 = y;
        }
        return 0.0;
    }
}

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
struct Node {
    int l = 0, r = 0, cnt = 0;
    int length = 0;
};

class SegmentTree {
private:
    vector<Node> tr;
    vector<int> nums;

    void build(int u, int l, int r) {
        tr[u].l = l;
        tr[u].r = r;
        if (l != r) {
            int mid = (l + r) >> 1;
            build(u << 1, l, mid);
            build(u << 1 | 1, mid + 1, r);
        }
    }

    void pushup(int u) {
        if (tr[u].cnt > 0) {
            tr[u].length = nums[tr[u].r + 1] - nums[tr[u].l];
        } else if (tr[u].l == tr[u].r) {
            tr[u].length = 0;
        } else {
            tr[u].length = tr[u << 1].length + tr[u << 1 | 1].length;
        }
    }

public:
    SegmentTree(const vector<int>& nums)
        : nums(nums) {
        int n = (int) nums.size() - 1;
        tr.assign(n << 2, Node());
        build(1, 0, n - 1);
    }

    void modify(int u, int l, int r, int k) {
        if (tr[u].l >= l && tr[u].r <= r) {
            tr[u].cnt += k;
        } else {
            int mid = (tr[u].l + tr[u].r) >> 1;
            if (l <= mid) modify(u << 1, l, r, k);
            if (r > mid) modify(u << 1 | 1, l, r, k);
        }
        pushup(u);
    }

    int query() const {
        return tr[1].length;
    }
};

class Solution {
public:
    double separateSquares(vector<vector<int>>& squares) {
        set<int> xs;
        vector<array<int, 4>> segs;

        for (auto& sq : squares) {
            int x1 = sq[0], y1 = sq[1], l = sq[2];
            int x2 = x1 + l, y2 = y1 + l;
            xs.insert(x1);
            xs.insert(x2);
            segs.push_back({y1, x1, x2, 1});
            segs.push_back({y2, x1, x2, -1});
        }

        sort(segs.begin(), segs.end(), [](const auto& a, const auto& b) {
            return a[0] < b[0];
        });

        vector<int> st;
        st.reserve(xs.size());
        for (int x : xs) st.push_back(x);

        SegmentTree tree(st);

        unordered_map<int, int> d;
        d.reserve(st.size() * 2);
        for (int i = 0; i < (int) st.size(); i++) d[st[i]] = i;

        double area = 0.0;
        int y0 = 0;
        for (auto& s : segs) {
            int y = s[0], x1 = s[1], x2 = s[2], k = s[3];
            area += (double) (y - y0) * tree.query();
            tree.modify(1, d[x1], d[x2] - 1, k);
            y0 = y;
        }

        double target = area / 2.0;
        area = 0.0;
        y0 = 0;
        for (auto& s : segs) {
            int y = s[0], x1 = s[1], x2 = s[2], k = s[3];
            double t = (double) (y - y0) * tree.query();
            if (area + t >= target) {
                return y0 + (target - area) / tree.query();
            }
            area += t;
            tree.modify(1, d[x1], d[x2] - 1, k);
            y0 = y;
        }

        return 0.0;
    }
};

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
type Node struct {
    l, r   int
    cnt    int
    length int
}

type SegmentTree struct {
    tr   []Node
    nums []int
}

func NewSegmentTree(nums []int) *SegmentTree {
    n := len(nums) - 1
    tr := make([]Node, n<<2)
    t := &SegmentTree{tr: tr, nums: nums}
    t.build(1, 0, n-1)
    return t
}

func (t *SegmentTree) build(u, l, r int) {
    t.tr[u].l = l
    t.tr[u].r = r
    if l != r {
        mid := (l + r) >> 1
        t.build(u<<1, l, mid)
        t.build(u<<1|1, mid+1, r)
    }
}

func (t *SegmentTree) modify(u, l, r, k int) {
    if l > r {
        return
    }
    if t.tr[u].l >= l && t.tr[u].r <= r {
        t.tr[u].cnt += k
    } else {
        mid := (t.tr[u].l + t.tr[u].r) >> 1
        if l <= mid {
            t.modify(u<<1, l, r, k)
        }
        if r > mid {
            t.modify(u<<1|1, l, r, k)
        }
    }
    t.pushup(u)
}

func (t *SegmentTree) pushup(u int) {
    if t.tr[u].cnt > 0 {
        t.tr[u].length = t.nums[t.tr[u].r+1] - t.nums[t.tr[u].l]
    } else if t.tr[u].l == t.tr[u].r {
        t.tr[u].length = 0
    } else {
        t.tr[u].length = t.tr[u<<1].length + t.tr[u<<1|1].length
    }
}

func (t *SegmentTree) query() int {
    return t.tr[1].length
}

func separateSquares(squares [][]int) float64 {
    pos := make(map[int]bool)
    xs := make([]int, 0)
    segs := make([][]int, 0, len(squares)*2)
    for _, sq := range squares {
        x1, y1, l := sq[0], sq[1], sq[2]
        x2, y2 := x1+l, y1+l
        if !pos[x1] {
            pos[x1] = true
            xs = append(xs, x1)
        }
        if !pos[x2] {
            pos[x2] = true
            xs = append(xs, x2)
        }
        segs = append(segs, []int{y1, x1, x2, 1})
        segs = append(segs, []int{y2, x1, x2, -1})
    }
    sort.Slice(segs, func(i, j int) bool { return segs[i][0] < segs[j][0] })
    sort.Ints(xs)
    tree := NewSegmentTree(xs)
    d := make(map[int]int, len(xs))
    for i, x := range xs {
        d[x] = i
    }
    area := 0.0
    y0 := 0
    for _, s := range segs {
        y, x1, x2, k := s[0], s[1], s[2], s[3]
        area += float64(y-y0) * float64(tree.query())
        tree.modify(1, d[x1], d[x2]-1, k)
        y0 = y
    }
    target := area / 2.0
    area = 0.0
    y0 = 0
    for _, s := range segs {
        y, x1, x2, k := s[0], s[1], s[2], s[3]
        curLen := tree.query()
        t := float64(y-y0) * float64(curLen)
        if area+t >= target {
            return float64(y0) + (target-area)/float64(curLen)
        }
        area += t
        tree.modify(1, d[x1], d[x2]-1, k)
        y0 = y
    }
    return 0.0
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
class Node {
    l = 0;
    r = 0;
    cnt = 0;
    length = 0;
}

class SegmentTree {
    private tr: Node[];
    private nums: number[];
    constructor(nums: number[]) {
        this.nums = nums;
        const n = nums.length - 1;
        this.tr = Array.from({ length: n << 2 }, () => new Node());
        this.build(1, 0, n - 1);
    }

    private build(u: number, l: number, r: number): void {
        this.tr[u].l = l;
        this.tr[u].r = r;
        if (l !== r) {
            const mid = (l + r) >> 1;
            this.build(u << 1, l, mid);
            this.build((u << 1) | 1, mid + 1, r);
        }
    }

    modify(u: number, l: number, r: number, k: number): void {
        if (l > r) return;
        if (this.tr[u].l >= l && this.tr[u].r <= r) {
            this.tr[u].cnt += k;
        } else {
            const mid = (this.tr[u].l + this.tr[u].r) >> 1;
            if (l <= mid) this.modify(u << 1, l, r, k);
            if (r > mid) this.modify((u << 1) | 1, l, r, k);
        }
        this.pushup(u);
    }

    private pushup(u: number): void {
        if (this.tr[u].cnt > 0) {
            this.tr[u].length = this.nums[this.tr[u].r + 1] - this.nums[this.tr[u].l];
        } else if (this.tr[u].l === this.tr[u].r) {
            this.tr[u].length = 0;
        } else {
            this.tr[u].length = this.tr[u << 1].length + this.tr[(u << 1) | 1].length;
        }
    }

    query(): number {
        return this.tr[1].length;
    }
}

function separateSquares(squares: number[][]): number {
    const xsSet = new Set<number>();
    const segs: number[][] = [];
    for (const [x1, y1, l] of squares) {
        const [x2, y2] = [x1 + l, y1 + l];
        xsSet.add(x1);
        xsSet.add(x2);
        segs.push([y1, x1, x2, 1]);
        segs.push([y2, x1, x2, -1]);
    }
    segs.sort((a, b) => a[0] - b[0]);
    const xs = Array.from(xsSet);
    xs.sort((a, b) => a - b);
    const tree = new SegmentTree(xs);
    const d = new Map<number, number>();
    for (let i = 0; i < xs.length; i++) {
        d.set(xs[i], i);
    }
    let area = 0.0;
    let y0 = 0;
    for (const [y, x1, x2, k] of segs) {
        area += (y - y0) * tree.query();
        tree.modify(1, d.get(x1)!, d.get(x2)! - 1, k);
        y0 = y;
    }
    const target = area / 2.0;
    area = 0.0;
    y0 = 0;
    for (const [y, x1, x2, k] of segs) {
        const curLen = tree.query();
        const t = (y - y0) * curLen;
        if (area + t >= target) {
            return y0 + (target - area) / curLen;
        }
        area += t;
        tree.modify(1, d.get(x1)!, d.get(x2)! - 1, k);
        y0 = y;
    }
    return 0.0;
}

评论