3453. 分割正方形 I

题目描述

给你一个二维整数数组 squares ，其中 squares[i] = [x_i, y_i, l_i] 表示一个与 x 轴平行的正方形的左下角坐标和正方形的边长。

找到一个最小的 y 坐标，它对应一条水平线，该线需要满足它以上正方形的总面积等于该线以下正方形的总面积。

答案如果与实际答案的误差在 10^-5 以内，将视为正确答案。

注意：正方形 可能会 重叠。重叠区域应该被 多次计数 。

示例 1：

输入： squares = [[0,0,1],[2,2,1]]

输出： 1.00000

解释：

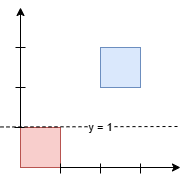
任何在 y = 1 和 y = 2 之间的水平线都会有 1 平方单位的面积在其上方，1 平方单位的面积在其下方。最小的 y 坐标是 1。

示例 2：

输入： squares = [[0,0,2],[1,1,1]]

输出： 1.16667

解释：

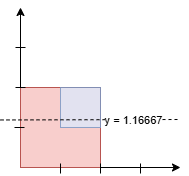
面积如下：

线下的面积：7/6 * 2 (红色) + 1/6 (蓝色) = 15/6 = 2.5。
线上的面积：5/6 * 2 (红色) + 5/6 (蓝色) = 15/6 = 2.5。

由于线以上和线以下的面积相等，输出为 7/6 = 1.16667。

提示：

1 <= squares.length <= 5 * 10⁴
squares[i] = [x_i, y_i, l_i]
squares[i].length == 3
0 <= x_i, y_i <= 10⁹
1 <= l_i <= 10⁹
所有正方形的总面积不超过 10¹²。

解法

方法一：二分查找

根据题意，我们需要找到一个水平线，使得该线以上正方形的总面积等于该线以下正方形的总面积。由于随着 \(y\) 坐标的增加，线以下的面积会增加，线以上的面积会减少，因此我们可以使用二分查找来找到这个水平线的 \(y\) 坐标。

我们定义二分查找的左边界 \(l = 0\)，右边界 \(r = \max(y_i + l_i)\)，即所有正方形的最高点。然后我们计算中间点 \(mid = (l + r) / 2\)，并计算该水平线以下的面积。如果该面积大于等于总面积的一半，则说明我们需要向下移动右边界 \(r\)，否则向上移动左边界 \(l\)。我们重复这个过程，直到左右边界的差小于一个很小的值（例如 \(10^{-5}\)）。

时间复杂度 \(O(n \log(MU))\)，其中 \(n\) 是正方形的数量，而 \(M = 10^5\), \(U = \max(y_i + l_i)\)。空间复杂度 \(O(1)\)。

Python3JavaC++GoTypeScriptRust

class Solution:
    def separateSquares(self, squares: List[List[int]]) -> float:
        def check(y1: float) -> bool:
            t = 0
            for _, y, l in squares:
                if y < y1:
                    t += l * min(y1 - y, l)
            return t >= s / 2

        s = sum(a[2] * a[2] for a in squares)
        l, r = 0, max(a[1] + a[2] for a in squares)
        eps = 1e-5
        while r - l > eps:
            mid = (l + r) / 2
            if check(mid):
                r = mid
            else:
                l = mid
        return r

class Solution {
    private int[][] squares;
    private double s;

    private boolean check(double y1) {
        double t = 0.0;
        for (int[] a : squares) {
            int y = a[1];
            int l = a[2];
            if (y < y1) {
                t += (double) l * Math.min(y1 - y, l);
            }
        }
        return t >= s / 2.0;
    }

    public double separateSquares(int[][] squares) {
        this.squares = squares;
        s = 0.0;
        double l = 0.0;
        double r = 0.0;
        for (int[] a : squares) {
            s += (double) a[2] * a[2];
            r = Math.max(r, a[1] + a[2]);
        }

        double eps = 1e-5;
        while (r - l > eps) {
            double mid = (l + r) / 2.0;
            if (check(mid)) {
                r = mid;
            } else {
                l = mid;
            }
        }
        return r;
    }
}

class Solution {
public:
    vector<vector<int>>* squares;
    double s;

    bool check(double y1) {
        double t = 0.0;
        for (const auto& a : *squares) {
            int y = a[1];
            int l = a[2];
            if (y < y1) {
                t += (double) l * min(y1 - y, (double) l);
            }
        }
        return t >= s / 2.0;
    }

    double separateSquares(vector<vector<int>>& squares) {
        this->squares = &squares;
        s = 0.0;
        double l = 0.0;
        double r = 0.0;
        for (const auto& a : squares) {
            s += (double) a[2] * a[2];
            r = max(r, (double) a[1] + a[2]);
        }
        const double eps = 1e-5;
        while (r - l > eps) {
            double mid = (l + r) / 2.0;
            if (check(mid)) {
                r = mid;
            } else {
                l = mid;
            }
        }
        return r;
    }
};

func separateSquares(squares [][]int) float64 {
    s := 0.0
    check := func(y1 float64) bool {
        t := 0.0
        for _, a := range squares {
            y := a[1]
            l := a[2]
            if float64(y) < y1 {
                h := min(float64(l), y1-float64(y))
                t += float64(l) * h
            }
        }
        return t >= s/2.0
    }
    l, r := 0.0, 0.0
    for _, a := range squares {
        s += float64(a[2] * a[2])
        r = max(r, float64(a[1]+a[2]))
    }

    const eps = 1e-5
    for r-l > eps {
        mid := (l + r) / 2.0
        if check(mid) {
            r = mid
        } else {
            l = mid
        }
    }
    return r
}

function separateSquares(squares: number[][]): number {
    const check = (y1: number): boolean => {
        let t = 0;
        for (const [_, y, l] of squares) {
            if (y < y1) {
                t += l * Math.min(y1 - y, l);
            }
        }
        return t >= s / 2;
    };

    let s = 0;
    let l = 0;
    let r = 0;
    for (const a of squares) {
        s += a[2] * a[2];
        r = Math.max(r, a[1] + a[2]);
    }

    const eps = 1e-5;
    while (r - l > eps) {
        const mid = (l + r) / 2;
        if (check(mid)) {
            r = mid;
        } else {
            l = mid;
        }
    }
    return r;
}

impl Solution {
    pub fn separate_squares(squares: Vec<Vec<i32>>) -> f64 {
        let mut s: f64 = 0.0;

        let mut l: f64 = 0.0;
        let mut r: f64 = 0.0;

        for a in squares.iter() {
            let len = a[2] as f64;
            s += len * len;
            r = r.max((a[1] + a[2]) as f64);
        }

        let check = |y1: f64| -> bool {
            let mut t: f64 = 0.0;
            for a in squares.iter() {
                let y = a[1] as f64;
                let l = a[2] as f64;
                if y < y1 {
                    let h = l.min(y1 - y);
                    t += l * h;
                }
            }
            t >= s / 2.0
        };

        const EPS: f64 = 1e-5;
        while r - l > EPS {
            let mid = (l + r) / 2.0;
            if check(mid) {
                r = mid;
            } else {
                l = mid;
            }
        }
        r
    }
}

3453. 分割正方形 I

题目描述

解法

方法一：二分查找

评论