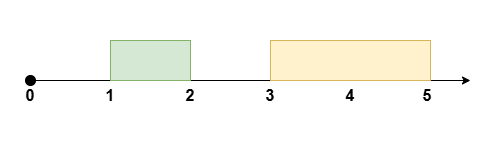题目描述
给你一个整数 eventTime 表示一个活动的总时长,这个活动开始于 t = 0 ,结束于 t = eventTime 。
同时给你两个长度为 n 的整数数组 startTime 和 endTime 。它们表示这次活动中 n 个时间 没有重叠 的会议,其中第 i 个会议的时间为 [startTime[i], endTime[i]] 。
你可以重新安排 至多 k 个会议,安排的规则是将会议时间平移,且保持原来的 会议时长 ,你的目的是移动会议后 最大化 相邻两个会议之间的 最长 连续空余时间。
移动前后所有会议之间的 相对 顺序需要保持不变,而且会议时间也需要保持互不重叠。
请你返回重新安排会议以后,可以得到的 最大 空余时间。
注意,会议 不能 安排到整个活动的时间以外。
示例 1:
输入:eventTime = 5, k = 1, startTime = [1,3], endTime = [2,5]
输出:2
解释:
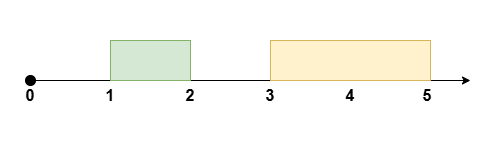
将 [1, 2] 的会议安排到 [2, 3] ,得到空余时间 [0, 2] 。
示例 2:
输入:eventTime = 10, k = 1, startTime = [0,2,9], endTime = [1,4,10]
输出:6
解释:
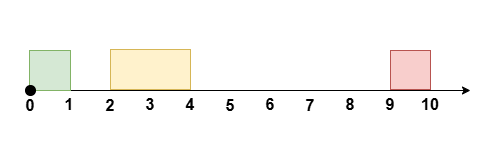
将 [2, 4] 的会议安排到 [1, 3] ,得到空余时间 [3, 9] 。
示例 3:
输入:eventTime = 5, k = 2, startTime = [0,1,2,3,4], endTime = [1,2,3,4,5]
输出:0
解释:
活动中的所有时间都被会议安排满了。
提示:
1 <= eventTime <= 109n == startTime.length == endTime.length2 <= n <= 1051 <= k <= n0 <= startTime[i] < endTime[i] <= eventTimeendTime[i] <= startTime[i + 1] 其中 i 在范围 [0, n - 2] 之间。
解法
方法一:滑动窗口
题目相当于把相邻的空闲时间段合并成一个更长的空闲时间段。一共有 \(n + 1\) 个空闲时间段,分别是:
- 第一个空闲时间段是从活动开始到第一个会议开始的时间段;
- 中间的 \(n - 1\) 个空闲时间段是相邻两个会议之间的时间段;
- 最后一个空闲时间段是最后一个会议结束到活动结束的时间段。
题目最多可以重新安排 \(k\) 个会议,等价于最多可以合并 \(k + 1\) 个空闲时间段。我们需要找到这 \(k + 1\) 个空闲时间段的最大长度。
我们可以将这些空闲时间段的长度存储在一个数组中 \(\textit{nums}\) 中。然后,我们一个长度为 \(k + 1\) 的滑动窗口,遍历这个数组,计算每个窗口的和,找到最大的和,即为所求的最大空闲时间。
时间复杂度 \(O(n)\),空间复杂度 \(O(n)\)。其中 \(n\) 是会议的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | class Solution:
def maxFreeTime(
self, eventTime: int, k: int, startTime: List[int], endTime: List[int]
) -> int:
nums = [startTime[0]]
for i in range(1, len(endTime)):
nums.append(startTime[i] - endTime[i - 1])
nums.append(eventTime - endTime[-1])
ans = s = 0
for i, x in enumerate(nums):
s += x
if i >= k:
ans = max(ans, s)
s -= nums[i - k]
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution {
public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {
int n = endTime.length;
int[] nums = new int[n + 1];
nums[0] = startTime[0];
for (int i = 1; i < n; ++i) {
nums[i] = startTime[i] - endTime[i - 1];
}
nums[n] = eventTime - endTime[n - 1];
int ans = 0, s = 0;
for (int i = 0; i <= n; ++i) {
s += nums[i];
if (i >= k) {
ans = Math.max(ans, s);
s -= nums[i - k];
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | class Solution {
public:
int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {
int n = endTime.size();
vector<int> nums(n + 1);
nums[0] = startTime[0];
for (int i = 1; i < n; ++i) {
nums[i] = startTime[i] - endTime[i - 1];
}
nums[n] = eventTime - endTime[n - 1];
int ans = 0, s = 0;
for (int i = 0; i <= n; ++i) {
s += nums[i];
if (i >= k) {
ans = max(ans, s);
s -= nums[i - k];
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {
n := len(endTime)
nums := make([]int, n+1)
nums[0] = startTime[0]
for i := 1; i < n; i++ {
nums[i] = startTime[i] - endTime[i-1]
}
nums[n] = eventTime - endTime[n-1]
ans, s := 0, 0
for i := 0; i <= n; i++ {
s += nums[i]
if i >= k {
ans = max(ans, s)
s -= nums[i-k]
}
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | function maxFreeTime(eventTime: number, k: number, startTime: number[], endTime: number[]): number {
const n = endTime.length;
const nums: number[] = new Array(n + 1);
nums[0] = startTime[0];
for (let i = 1; i < n; i++) {
nums[i] = startTime[i] - endTime[i - 1];
}
nums[n] = eventTime - endTime[n - 1];
let [ans, s] = [0, 0];
for (let i = 0; i <= n; i++) {
s += nums[i];
if (i >= k) {
ans = Math.max(ans, s);
s -= nums[i - k];
}
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | impl Solution {
pub fn max_free_time(event_time: i32, k: i32, start_time: Vec<i32>, end_time: Vec<i32>) -> i32 {
let n = end_time.len();
let mut nums = vec![0; n + 1];
nums[0] = start_time[0];
for i in 1..n {
nums[i] = start_time[i] - end_time[i - 1];
}
nums[n] = event_time - end_time[n - 1];
let mut ans = 0;
let mut s = 0;
for i in 0..=n {
s += nums[i];
if i as i32 >= k {
ans = ans.max(s);
s -= nums[i - k as usize];
}
}
ans
}
}
|
方法二:滑动窗口(空间优化)
在方法一中,我们使用了一个数组来存储空闲时间段的长度。实际上,我们不需要存储整个数组,可以用一个函数 \(f(i)\) 来表示第 \(i\) 个空闲时间段的长度。这样可以节省空间。
时间复杂度 \(O(n)\),其中 \(n\) 是会议的数量。空间复杂度 \(O(1)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | class Solution:
def maxFreeTime(
self, eventTime: int, k: int, startTime: List[int], endTime: List[int]
) -> int:
def f(i: int) -> int:
if i == 0:
return startTime[0]
if i == len(endTime):
return eventTime - endTime[-1]
return startTime[i] - endTime[i - 1]
ans = s = 0
for i in range(len(endTime) + 1):
s += f(i)
if i >= k:
ans = max(ans, s)
s -= f(i - k)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | class Solution {
public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {
int n = endTime.length;
IntUnaryOperator f = i -> {
if (i == 0) {
return startTime[0];
}
if (i == n) {
return eventTime - endTime[n - 1];
}
return startTime[i] - endTime[i - 1];
};
int ans = 0, s = 0;
for (int i = 0; i <= n; i++) {
s += f.applyAsInt(i);
if (i >= k) {
ans = Math.max(ans, s);
s -= f.applyAsInt(i - k);
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | class Solution {
public:
int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {
int n = endTime.size();
auto f = [&](int i) -> int {
if (i == 0) {
return startTime[0];
}
if (i == n) {
return eventTime - endTime[n - 1];
}
return startTime[i] - endTime[i - 1];
};
int ans = 0, s = 0;
for (int i = 0; i <= n; ++i) {
s += f(i);
if (i >= k) {
ans = max(ans, s);
s -= f(i - k);
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {
n := len(endTime)
f := func(i int) int {
if i == 0 {
return startTime[0]
}
if i == n {
return eventTime - endTime[n-1]
}
return startTime[i] - endTime[i-1]
}
ans, s := 0, 0
for i := 0; i <= n; i++ {
s += f(i)
if i >= k {
ans = max(ans, s)
s -= f(i - k)
}
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | function maxFreeTime(eventTime: number, k: number, startTime: number[], endTime: number[]): number {
const n = endTime.length;
const f = (i: number): number => {
if (i === 0) {
return startTime[0];
}
if (i === n) {
return eventTime - endTime[n - 1];
}
return startTime[i] - endTime[i - 1];
};
let ans = 0;
let s = 0;
for (let i = 0; i <= n; i++) {
s += f(i);
if (i >= k) {
ans = Math.max(ans, s);
s -= f(i - k);
}
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | impl Solution {
pub fn max_free_time(event_time: i32, k: i32, start_time: Vec<i32>, end_time: Vec<i32>) -> i32 {
let n = end_time.len();
let f = |i: usize| -> i32 {
if i == 0 {
start_time[0]
} else if i == n {
event_time - end_time[n - 1]
} else {
start_time[i] - end_time[i - 1]
}
};
let mut ans = 0;
let mut s = 0;
for i in 0..=n {
s += f(i);
if i >= k as usize {
ans = ans.max(s);
s -= f(i - k as usize);
}
}
ans
}
}
|