跳转至

3100. 换水问题 II

题目描述

给你两个整数 numBottles 和 numExchange 。

numBottles 代表你最初拥有的满水瓶数量。在一次操作中，你可以执行以下操作之一：

  • 喝掉任意数量的满水瓶，使它们变成空水瓶。
  • 用 numExchange 个空水瓶交换一个满水瓶。然后，将 numExchange 的值增加 1 。

注意，你不能使用相同的 numExchange 值交换多批空水瓶。例如，如果 numBottles == 3 并且 numExchange == 1 ，则不能用 3 个空水瓶交换成 3 个满水瓶。

返回你 最多 可以喝到多少瓶水。

 

示例 1：

输入：numBottles = 13, numExchange = 6
输出：15
解释：上表显示了满水瓶的数量、空水瓶的数量、numExchange 的值，以及累计喝掉的水瓶数量。

示例 2：

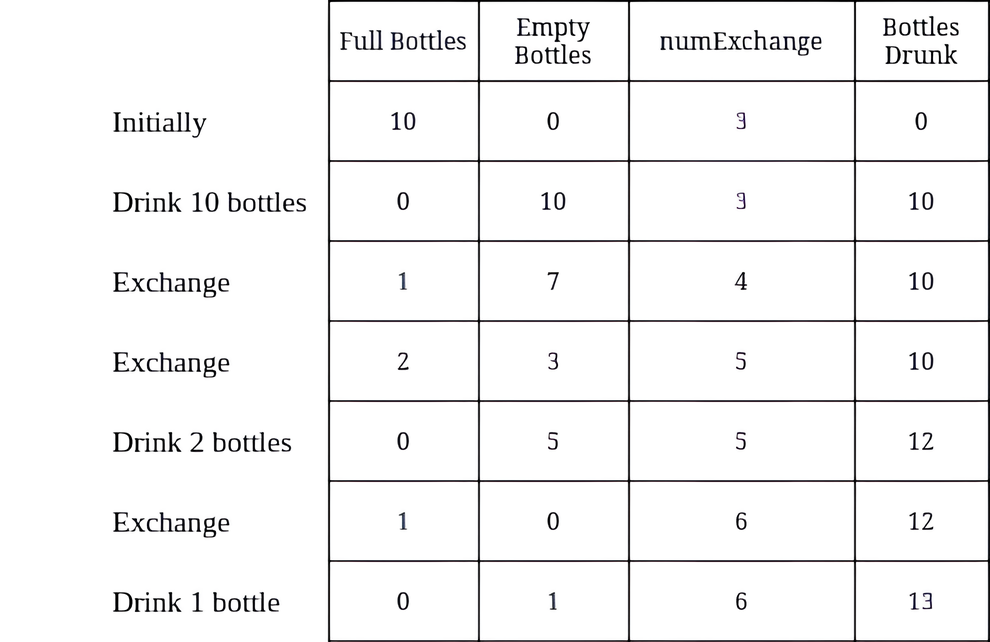
输入：numBottles = 10, numExchange = 3
输出：13
解释：上表显示了满水瓶的数量、空水瓶的数量、numExchange 的值，以及累计喝掉的水瓶数量。

 

提示：

  • 1 <= numBottles <= 100
  • 1 <= numExchange <= 100

解法

方法一：模拟

我们可以在一开始就喝掉所有的满水瓶，因此初始时我们喝到的水数量为 \(\textit{numBottles}\)。然后我们不断地进行以下操作：

  • 如果当前有 \(\textit{numExchange}\) 个空水瓶，我们就可以用它们换一瓶满水瓶，换完后，\(\textit{numExchange}\) 的值增加 \(1\)。然后，我们喝掉这瓶水，喝到的水数量增加 \(1\)，空水瓶数量增加 \(1\)。
  • 如果当前没有 \(\textit{numExchange}\) 个空水瓶，那么我们就不能再换水了，此时我们就可以停止操作。

我们不断地进行上述操作，直到我们无法再换水为止。最终我们喝到的水的数量就是答案。

时间复杂度 \(O(\sqrt{n})\)，其中 \(n\) 是初始的满水瓶数量。空间复杂度 \(O(1)\)。

1
2
3
4
5
6
7
8
9
class Solution:
    def maxBottlesDrunk(self, numBottles: int, numExchange: int) -> int:
        ans = numBottles
        while numBottles >= numExchange:
            numBottles -= numExchange
            numExchange += 1
            ans += 1
            numBottles += 1
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
    public int maxBottlesDrunk(int numBottles, int numExchange) {
        int ans = numBottles;
        while (numBottles >= numExchange) {
            numBottles -= numExchange;
            ++numExchange;
            ++ans;
            ++numBottles;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution {
public:
    int maxBottlesDrunk(int numBottles, int numExchange) {
        int ans = numBottles;
        while (numBottles >= numExchange) {
            numBottles -= numExchange;
            ++numExchange;
            ++ans;
            ++numBottles;
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
func maxBottlesDrunk(numBottles int, numExchange int) int {
    ans := numBottles
    for numBottles >= numExchange {
        numBottles -= numExchange
        numExchange++
        ans++
        numBottles++
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
function maxBottlesDrunk(numBottles: number, numExchange: number): number {
    let ans = numBottles;
    while (numBottles >= numExchange) {
        numBottles -= numExchange;
        ++numExchange;
        ++ans;
        ++numBottles;
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
impl Solution {
    pub fn max_bottles_drunk(mut num_bottles: i32, mut num_exchange: i32) -> i32 {
        let mut ans = num_bottles;

        while num_bottles >= num_exchange {
            num_bottles -= num_exchange;
            num_exchange += 1;
            ans += 1;
            num_bottles += 1;
        }

        ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
public class Solution {
    public int MaxBottlesDrunk(int numBottles, int numExchange) {
        int ans = numBottles;
        while (numBottles >= numExchange) {
            numBottles -= numExchange;
            ++numExchange;
            ++ans;
            ++numBottles;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
    /**
     * @param Integer $numBottles
     * @param Integer $numExchange
     * @return Integer
     */
    function maxBottlesDrunk($numBottles, $numExchange) {
        $ans = $numBottles;
        while ($numBottles >= $numExchange) {
            $numBottles -= $numExchange;
            $numExchange++;
            $ans++;
            $numBottles++;
        }
        return $ans;
    }
}

评论