二叉树 树 深度优先搜索
题目描述 给定一个二叉树的根节点 root 和整数 k。除了左右孩子之外,该树的每个节点还有另外两个属性:一个仅包含小写英文字母(可能为空)的 字符串 node.val 和一个非负整数 node.len。这棵树中有两种类型的节点:
叶子节点 :这些节点没有子节点,node.len = 0,node.val 是一个 非空 字符串。内部节点 :这些节点至少有一个子节点(最多两个子节点),node.len > 0,node.val 是一个 空 字符串。 上述描述的树被称为 Rope 二叉树。现在我们用以下递归方式定义 S[node]:
如果 node 是一个叶子节点,则 S[node] = node.val, 否则,如果 node 是一个内部节点,则 S[node] = concat(S[node.left], S[node.right]),且 S[node].length = node.len。 返回字符串 S[root] 的第 k 个字符。
注意 :如果 s 和 p 是两个字符串,则 concat(s, p) 是将字符串 p 连接到 s 后面的字符串。例如,concat("ab", "zz") = "abzz"。
示例 1:
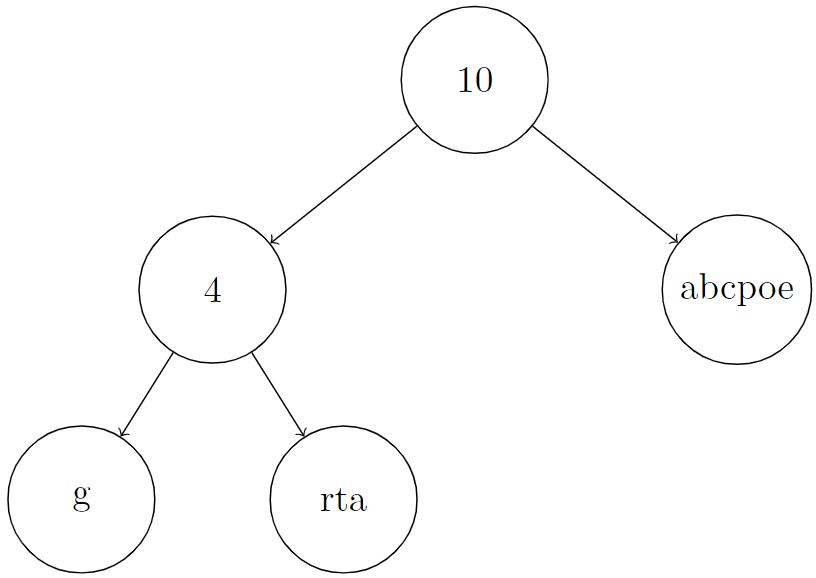
输入: root = [10,4,"abcpoe","g","rta"], k = 6
输出: "b"
解释: 在下面的图片中,我们在内部节点上放置一个表示 node.len 的整数,在叶子节点上放置一个表示 node.val 的字符串。 你可以看到,S[root] = concat(concat("g", "rta"), "abcpoe") = "grtaabcpoe"。因此,S[root][5],表示它的第6个字符,等于 "b"。
示例 2:
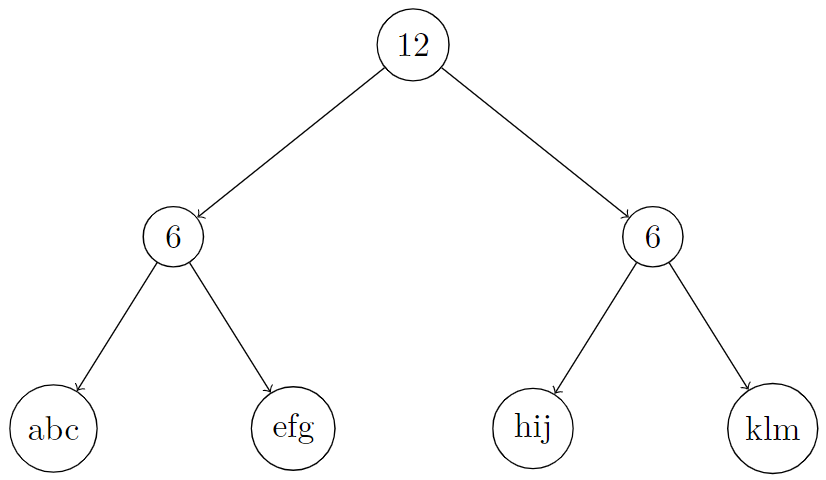
输入: root = [12,6,6,"abc","efg","hij","klm"], k = 3
输出: "c"
解释: 在下面的图片中,我们在内部节点上放置一个表示 node.len 的整数,在叶子节点上放置一个表示 node.val 的字符串。 你可以看到,S[root] = concat(concat("abc", "efg"), concat("hij", "klm")) = "abcefghijklm"。因此,S[root][2],表示它的第3个字符,等于 "c"。
示例 3:
输入: root = ["ropetree"], k = 8
输出: "e"
解释: 在下面的图片中,我们在内部节点上放置一个表示 node.len 的整数,在叶子节点上放置一个表示 node.val 的字符串。 你可以看到,S[root] = "ropetree"。因此,S[root][7],表示它的第8个字符,等于 "e"。
提示:
这棵树的节点数量在区间 [1, 103 ] node.val 仅包含小写英文字母0 <= node.val.length <= 500 <= node.len <= 104 对于叶子节点, node.len = 0 且 node.val 是非空的 对于内部节点, node.len > 0 且 node.val 为空 1 <= k <= S[root].length 解法 方法一:DFS 我们可以使用深度优先搜索的方法,定义一个函数 \(dfs(root)\) ,表示从根节点开始搜索,返回以 \(root\) 为根节点的子树的字符串。那么答案就是 \(dfs(root)[k-1]\) 。
函数 \(dfs(root)\) 的执行逻辑如下:
如果 \(root\) 为空,返回空字符串; 如果 \(root\) 是叶子节点,返回 \(root.val\) ; 否则,返回 \(dfs(root.left) + dfs(root.right)\) 。 时间复杂度 \(O(n^2)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 是树中节点的个数。
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 # Definition for a rope tree node.
# class RopeTreeNode(object):
# def __init__(self, len=0, val="", left=None, right=None):
# self.len = len
# self.val = val
# self.left = left
# self.right = right
class Solution :
def getKthCharacter ( self , root : Optional [ object ], k : int ) -> str :
def dfs ( root ):
if root is None :
return ""
if root . len == 0 :
return root . val
return dfs ( root . left ) + dfs ( root . right )
return dfs ( root )[ k - 1 ]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 /**
* Definition for a rope tree node.
* class RopeTreeNode {
* int len;
* String val;
* RopeTreeNode left;
* RopeTreeNode right;
* RopeTreeNode() {}
* RopeTreeNode(String val) {
* this.len = 0;
* this.val = val;
* }
* RopeTreeNode(int len) {
* this.len = len;
* this.val = "";
* }
* RopeTreeNode(int len, TreeNode left, TreeNode right) {
* this.len = len;
* this.val = "";
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public char getKthCharacter ( RopeTreeNode root , int k ) {
return dfs ( root ). charAt ( k - 1 );
}
private String dfs ( RopeTreeNode root ) {
if ( root == null ) {
return "" ;
}
if ( root . val . length () > 0 ) {
return root . val ;
}
String left = dfs ( root . left );
String right = dfs ( root . right );
return left + right ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 /**
* Definition for a rope tree node.
* struct RopeTreeNode {
* int len;
* string val;
* RopeTreeNode *left;
* RopeTreeNode *right;
* RopeTreeNode() : len(0), val(""), left(nullptr), right(nullptr) {}
* RopeTreeNode(string s) : len(0), val(std::move(s)), left(nullptr), right(nullptr) {}
* RopeTreeNode(int x) : len(x), val(""), left(nullptr), right(nullptr) {}
* RopeTreeNode(int x, RopeTreeNode *left, RopeTreeNode *right) : len(x), val(""), left(left), right(right) {}
* };
*/
class Solution {
public :
char getKthCharacter ( RopeTreeNode * root , int k ) {
function < string ( RopeTreeNode * root ) > dfs = [ & ]( RopeTreeNode * root ) -> string {
if ( root == nullptr ) {
return "" ;
}
if ( root -> len == 0 ) {
return root -> val ;
}
string left = dfs ( root -> left );
string right = dfs ( root -> right );
return left + right ;
};
return dfs ( root )[ k - 1 ];
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 /**
* Definition for a rope tree node.
* type RopeTreeNode struct {
* len int
* val string
* left *RopeTreeNode
* right *RopeTreeNode
* }
*/
func getKthCharacter ( root * RopeTreeNode , k int ) byte {
var dfs func ( root * RopeTreeNode ) string
dfs = func ( root * RopeTreeNode ) string {
if root == nil {
return ""
}
if root . len == 0 {
return root . val
}
left , right := dfs ( root . left ), dfs ( root . right )
return left + right
}
return dfs ( root )[ k - 1 ]
}
GitHub