


题目描述
给你一个正整数 n ,表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ,矩阵中填满了 0 。
另给你一个二维整数数组 query 。针对每个查询 query[i] = [row1i, col1i, row2i, col2i] ,请你执行下述操作:
- 找出 左上角 为
(row1i, col1i) 且 右下角 为 (row2i, col2i) 的子矩阵,将子矩阵中的 每个元素 加 1 。也就是给所有满足 row1i <= x <= row2i 和 col1i <= y <= col2i 的 mat[x][y] 加 1 。
返回执行完所有操作后得到的矩阵 mat 。
示例 1:
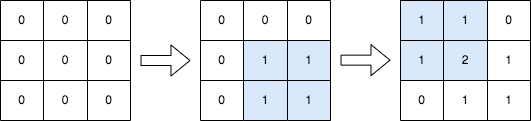
输入:n = 3, queries = [[1,1,2,2],[0,0,1,1]]
输出:[[1,1,0],[1,2,1],[0,1,1]]
解释:上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵、执行完第二个操作后的矩阵。
- 第一个操作:将左上角为 (1, 1) 且右下角为 (2, 2) 的子矩阵中的每个元素加 1 。
- 第二个操作:将左上角为 (0, 0) 且右下角为 (1, 1) 的子矩阵中的每个元素加 1 。
示例 2:

输入:n = 2, queries = [[0,0,1,1]]
输出:[[1,1],[1,1]]
解释:上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵。
- 第一个操作:将矩阵中的每个元素加 1 。
提示:
1 <= n <= 5001 <= queries.length <= 1040 <= row1i <= row2i < n0 <= col1i <= col2i < n
解法
方法一:二维差分
二维差分数组是一种用于高效处理二维数组区间更新的技巧。我们可以通过维护一个与原矩阵大小相同的差分矩阵来实现对子矩阵的快速更新。
假设我们有一个二维差分矩阵 \(\textit{diff}\),初始时所有元素均为 \(0\)。对于每个查询 \([\textit{row1}, \textit{col1}, \textit{row2}, \textit{col2}]\),我们可以通过以下步骤更新差分矩阵:
- 在位置 \((\textit{row1}, \textit{col1})\) 加 \(1\)。
- 在位置 \((\textit{row2} + 1, \textit{col1})\) 减 \(1\),前提是 \(\textit{row2} + 1 < n\)。
- 在位置 \((\textit{row1}, \textit{col2} + 1)\) 减 \(1\),前提是 \(\textit{col2} + 1 < n\)。
- 在位置 \((\textit{row2} + 1, \textit{col2} + 1)\) 加 \(1\),前提是 \(\textit{row2} + 1 < n\) 且 \(\textit{col2} + 1 < n\)。
完成所有查询后,我们需要通过前缀和的方式将差分矩阵转换回原矩阵。即,对于每个位置 \((i, j)\),我们计算:
\[ \textit{mat}[i][j] = \textit{diff}[i][j] + (\textit{mat}[i-1][j] \text{ if } i > 0 \text{ else } 0) + (\textit{mat}[i][j-1] \text{ if } j > 0 \text{ else } 0) - (\textit{mat}[i-1][j-1] \text{ if } i > 0 \text{ and } j > 0 \text{ else } 0) \]
时间复杂度 \(O(m + n^2)\),其中 \(m\) 和 \(n\) 分别是 \(\textit{queries}\) 的长度和给定的 \(n\)。忽略答案的空间消耗,空间复杂度 \(O(1)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution:
def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:
mat = [[0] * n for _ in range(n)]
for x1, y1, x2, y2 in queries:
mat[x1][y1] += 1
if x2 + 1 < n:
mat[x2 + 1][y1] -= 1
if y2 + 1 < n:
mat[x1][y2 + 1] -= 1
if x2 + 1 < n and y2 + 1 < n:
mat[x2 + 1][y2 + 1] += 1
for i in range(n):
for j in range(n):
if i:
mat[i][j] += mat[i - 1][j]
if j:
mat[i][j] += mat[i][j - 1]
if i and j:
mat[i][j] -= mat[i - 1][j - 1]
return mat
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 | class Solution {
public int[][] rangeAddQueries(int n, int[][] queries) {
int[][] mat = new int[n][n];
for (var q : queries) {
int x1 = q[0], y1 = q[1], x2 = q[2], y2 = q[3];
mat[x1][y1]++;
if (x2 + 1 < n) {
mat[x2 + 1][y1]--;
}
if (y2 + 1 < n) {
mat[x1][y2 + 1]--;
}
if (x2 + 1 < n && y2 + 1 < n) {
mat[x2 + 1][y2 + 1]++;
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (i > 0) {
mat[i][j] += mat[i - 1][j];
}
if (j > 0) {
mat[i][j] += mat[i][j - 1];
}
if (i > 0 && j > 0) {
mat[i][j] -= mat[i - 1][j - 1];
}
}
}
return mat;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | class Solution {
public:
vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
vector<vector<int>> mat(n, vector<int>(n));
for (auto& q : queries) {
int x1 = q[0], y1 = q[1], x2 = q[2], y2 = q[3];
mat[x1][y1]++;
if (x2 + 1 < n) {
mat[x2 + 1][y1]--;
}
if (y2 + 1 < n) {
mat[x1][y2 + 1]--;
}
if (x2 + 1 < n && y2 + 1 < n) {
mat[x2 + 1][y2 + 1]++;
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (i > 0) {
mat[i][j] += mat[i - 1][j];
}
if (j > 0) {
mat[i][j] += mat[i][j - 1];
}
if (i > 0 && j > 0) {
mat[i][j] -= mat[i - 1][j - 1];
}
}
}
return mat;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | func rangeAddQueries(n int, queries [][]int) [][]int {
mat := make([][]int, n)
for i := range mat {
mat[i] = make([]int, n)
}
for _, q := range queries {
x1, y1, x2, y2 := q[0], q[1], q[2], q[3]
mat[x1][y1]++
if x2+1 < n {
mat[x2+1][y1]--
}
if y2+1 < n {
mat[x1][y2+1]--
}
if x2+1 < n && y2+1 < n {
mat[x2+1][y2+1]++
}
}
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
if i > 0 {
mat[i][j] += mat[i-1][j]
}
if j > 0 {
mat[i][j] += mat[i][j-1]
}
if i > 0 && j > 0 {
mat[i][j] -= mat[i-1][j-1]
}
}
}
return mat
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | function rangeAddQueries(n: number, queries: number[][]): number[][] {
const mat: number[][] = Array.from({ length: n }, () => Array(n).fill(0));
for (const [x1, y1, x2, y2] of queries) {
mat[x1][y1] += 1;
if (x2 + 1 < n) mat[x2 + 1][y1] -= 1;
if (y2 + 1 < n) mat[x1][y2 + 1] -= 1;
if (x2 + 1 < n && y2 + 1 < n) mat[x2 + 1][y2 + 1] += 1;
}
for (let i = 0; i < n; ++i) {
for (let j = 0; j < n; ++j) {
if (i > 0) mat[i][j] += mat[i - 1][j];
if (j > 0) mat[i][j] += mat[i][j - 1];
if (i > 0 && j > 0) mat[i][j] -= mat[i - 1][j - 1];
}
}
return mat;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 | impl Solution {
pub fn range_add_queries(n: i32, queries: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
let n = n as usize;
let mut mat = vec![vec![0; n]; n];
for q in queries {
let (x1, y1, x2, y2) = (q[0] as usize, q[1] as usize, q[2] as usize, q[3] as usize);
mat[x1][y1] += 1;
if x2 + 1 < n {
mat[x2 + 1][y1] -= 1;
}
if y2 + 1 < n {
mat[x1][y2 + 1] -= 1;
}
if x2 + 1 < n && y2 + 1 < n {
mat[x2 + 1][y2 + 1] += 1;
}
}
for i in 0..n {
for j in 0..n {
if i > 0 {
mat[i][j] += mat[i - 1][j];
}
if j > 0 {
mat[i][j] += mat[i][j - 1];
}
if i > 0 && j > 0 {
mat[i][j] -= mat[i - 1][j - 1];
}
}
}
mat
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | public class Solution {
public int[][] RangeAddQueries(int n, int[][] queries) {
int[][] mat = new int[n][];
for (int i = 0; i < n; i++) {
mat[i] = new int[n];
}
foreach (var q in queries) {
int x1 = q[0], y1 = q[1], x2 = q[2], y2 = q[3];
mat[x1][y1]++;
if (x2 + 1 < n) {
mat[x2 + 1][y1]--;
}
if (y2 + 1 < n) {
mat[x1][y2 + 1]--;
}
if (x2 + 1 < n && y2 + 1 < n) {
mat[x2 + 1][y2 + 1]++;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i > 0) {
mat[i][j] += mat[i - 1][j];
}
if (j > 0) {
mat[i][j] += mat[i][j - 1];
}
if (i > 0 && j > 0) {
mat[i][j] -= mat[i - 1][j - 1];
}
}
}
return mat;
}
}
|




