数组 模拟 矩阵
题目描述 给你一个下标从 0 开始的 m x n 二进制矩阵 grid 。
我们按照如下过程,定义一个下标从 0 开始的 m x n 差值矩阵 diff :
令第 i 行一的数目为 onesRowi 。 令第 j 列一的数目为 onesColj 。 令第 i 行零的数目为 zerosRowi 。 令第 j 列零的数目为 zerosColj 。 diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj 请你返回差值矩阵 diff 。
示例 1:
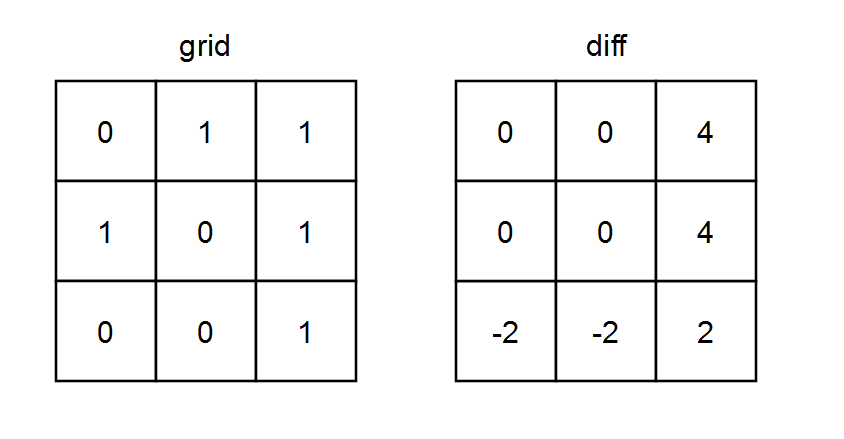
输入: grid = [[0,1,1],[1,0,1],[0,0,1]]
输出: [[0,0,4],[0,0,4],[-2,-2,2]]
解释:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 2 + 1 - 1 - 2 = 0
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 2 + 1 - 1 - 2 = 0
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 2 + 3 - 1 - 0 = 4
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 2 + 1 - 1 - 2 = 0
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 2 + 1 - 1 - 2 = 0
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 2 + 3 - 1 - 0 = 4
- diff[2][0] = onesRow2 + onesCol0 - zerosRow2 - zerosCol0 = 1 + 1 - 2 - 2 = -2
- diff[2][1] = onesRow2 + onesCol1 - zerosRow2 - zerosCol1 = 1 + 1 - 2 - 2 = -2
- diff[2][2] = onesRow2 + onesCol2 - zerosRow2 - zerosCol2 = 1 + 3 - 2 - 0 = 2
示例 2:
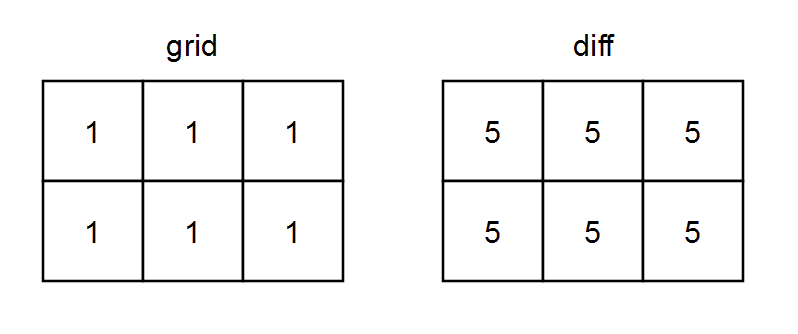
输入: grid = [[1,1,1],[1,1,1]]
输出: [[5,5,5],[5,5,5]]
解释:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 105 1 <= m * n <= 105 grid[i][j] 要么是 0 ,要么是 1 。 解法 方法一:模拟 根据题意模拟即可。
时间复杂度 \(O(m \times n)\) ,忽略答案的空间消耗,空间复杂度 \(O(m + n)\) 。其中 \(m\) 和 \(n\) 分别为矩阵的行数和列数。
Python3 Java C++ Go TypeScript Rust C
1
2
3
4
5
6
7
8
9
10
11
12
13
14 class Solution :
def onesMinusZeros ( self , grid : List [ List [ int ]]) -> List [ List [ int ]]:
m , n = len ( grid ), len ( grid [ 0 ])
rows = [ 0 ] * m
cols = [ 0 ] * n
for i , row in enumerate ( grid ):
for j , v in enumerate ( row ):
rows [ i ] += v
cols [ j ] += v
diff = [[ 0 ] * n for _ in range ( m )]
for i , r in enumerate ( rows ):
for j , c in enumerate ( cols ):
diff [ i ][ j ] = r + c - ( n - r ) - ( m - c )
return diff
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 class Solution {
public int [][] onesMinusZeros ( int [][] grid ) {
int m = grid . length , n = grid [ 0 ] . length ;
int [] rows = new int [ m ] ;
int [] cols = new int [ n ] ;
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
int v = grid [ i ][ j ] ;
rows [ i ] += v ;
cols [ j ] += v ;
}
}
int [][] diff = new int [ m ][ n ] ;
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
diff [ i ][ j ] = rows [ i ] + cols [ j ] - ( n - rows [ i ] ) - ( m - cols [ j ] );
}
}
return diff ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 class Solution {
public :
vector < vector < int >> onesMinusZeros ( vector < vector < int >>& grid ) {
int m = grid . size (), n = grid [ 0 ]. size ();
vector < int > rows ( m );
vector < int > cols ( n );
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
int v = grid [ i ][ j ];
rows [ i ] += v ;
cols [ j ] += v ;
}
}
vector < vector < int >> diff ( m , vector < int > ( n ));
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
diff [ i ][ j ] = rows [ i ] + cols [ j ] - ( n - rows [ i ]) - ( m - cols [ j ]);
}
}
return diff ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 func onesMinusZeros ( grid [][] int ) [][] int {
m , n := len ( grid ), len ( grid [ 0 ])
rows := make ([] int , m )
cols := make ([] int , n )
diff := make ([][] int , m )
for i , row := range grid {
diff [ i ] = make ([] int , n )
for j , v := range row {
rows [ i ] += v
cols [ j ] += v
}
}
for i , r := range rows {
for j , c := range cols {
diff [ i ][ j ] = r + c - ( n - r ) - ( m - c )
}
}
return diff
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 function onesMinusZeros ( grid : number [][]) : number [][] {
const m = grid . length ;
const n = grid [ 0 ]. length ;
const rows = new Array ( m ). fill ( 0 );
const cols = new Array ( n ). fill ( 0 );
for ( let i = 0 ; i < m ; i ++ ) {
for ( let j = 0 ; j < n ; j ++ ) {
if ( grid [ i ][ j ]) {
rows [ i ] ++ ;
cols [ j ] ++ ;
}
}
}
const ans = Array . from ({ length : m }, () => new Array ( n ). fill ( 0 ));
for ( let i = 0 ; i < m ; i ++ ) {
for ( let j = 0 ; j < n ; j ++ ) {
ans [ i ][ j ] = rows [ i ] + cols [ j ] - ( m - rows [ i ]) - ( n - cols [ j ]);
}
}
return ans ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 impl Solution {
pub fn ones_minus_zeros ( grid : Vec < Vec < i32 >> ) -> Vec < Vec < i32 >> {
let m = grid . len ();
let n = grid [ 0 ]. len ();
let mut rows = vec! [ 0 ; m ];
let mut cols = vec! [ 0 ; n ];
for i in 0 .. m {
for j in 0 .. n {
if grid [ i ][ j ] == 1 {
rows [ i ] += 1 ;
cols [ j ] += 1 ;
}
}
}
let mut ans = vec! [ vec! [ 0 ; n ]; m ];
for i in 0 .. m {
for j in 0 .. n {
ans [ i ][ j ] = ( rows [ i ] + cols [ j ] - ( m - rows [ i ]) - ( n - cols [ j ])) as i32 ;
}
}
ans
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 /**
* Return an array of arrays of size *returnSize.
* The sizes of the arrays are returned as *returnColumnSizes array.
* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
*/
int ** onesMinusZeros ( int ** grid , int gridSize , int * gridColSize , int * returnSize , int ** returnColumnSizes ) {
int * rows = malloc ( sizeof ( int ) * gridSize );
int * cols = malloc ( sizeof ( int ) * gridColSize [ 0 ]);
memset ( rows , 0 , sizeof ( int ) * gridSize );
memset ( cols , 0 , sizeof ( int ) * gridColSize [ 0 ]);
for ( int i = 0 ; i < gridSize ; i ++ ) {
for ( int j = 0 ; j < gridColSize [ 0 ]; j ++ ) {
if ( grid [ i ][ j ]) {
rows [ i ] ++ ;
cols [ j ] ++ ;
}
}
}
int ** ans = malloc ( sizeof ( int * ) * gridSize );
for ( int i = 0 ; i < gridSize ; i ++ ) {
ans [ i ] = malloc ( sizeof ( int ) * gridColSize [ 0 ]);
for ( int j = 0 ; j < gridColSize [ 0 ]; j ++ ) {
ans [ i ][ j ] = rows [ i ] + cols [ j ] - ( gridSize - rows [ i ]) - ( gridColSize [ 0 ] - cols [ j ]);
}
}
* returnSize = gridSize ;
* returnColumnSizes = gridColSize ;
return ans ;
}
GitHub