


题目描述
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,每个节点 至多 有一条出边。
有向图用大小为 n 下标从 0 开始的数组 edges 表示,表示节点 i 有一条有向边指向 edges[i] 。如果节点 i 没有出边,那么 edges[i] == -1 。
同时给你两个节点 node1 和 node2 。
请你返回一个从 node1 和 node2 都能到达节点的编号,使节点 node1 和节点 node2 到这个节点的距离 较大值最小化。如果有多个答案,请返回 最小 的节点编号。如果答案不存在,返回 -1 。
注意 edges 可能包含环。
示例 1:
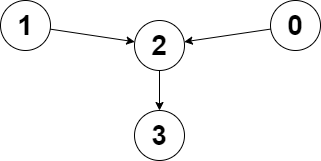
输入:edges = [2,2,3,-1], node1 = 0, node2 = 1
输出:2
解释:从节点 0 到节点 2 的距离为 1 ,从节点 1 到节点 2 的距离为 1 。
两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值,所以我们返回节点 2 。
示例 2:
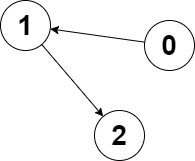
输入:edges = [1,2,-1], node1 = 0, node2 = 2
输出:2
解释:节点 0 到节点 2 的距离为 2 ,节点 2 到它自己的距离为 0 。
两个距离的较大值为 2 。我们无法得到一个比 2 更小的较大值,所以我们返回节点 2 。
提示:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i0 <= node1, node2 < n
解法
方法一:BFS + 枚举公共点
我们可以先用 BFS 求出从 \(node1\) 和 \(node2\) 分别到达每个点的距离,分别记为 \(d_1\) 和 \(d_2\)。然后枚举所有的公共点 \(i\),然后求出 \(\max(d_1[i], d_2[i])\),取其中的最小值即可。
时间复杂度 \(O(n)\),空间复杂度 \(O(n)\)。其中 \(n\) 为节点个数。
相似题目:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution:
def closestMeetingNode(self, edges: List[int], node1: int, node2: int) -> int:
def f(i):
dist = [inf] * n
dist[i] = 0
q = deque([i])
while q:
i = q.popleft()
for j in g[i]:
if dist[j] == inf:
dist[j] = dist[i] + 1
q.append(j)
return dist
g = defaultdict(list)
for i, j in enumerate(edges):
if j != -1:
g[i].append(j)
n = len(edges)
d1 = f(node1)
d2 = f(node2)
ans, d = -1, inf
for i, (a, b) in enumerate(zip(d1, d2)):
if (t := max(a, b)) < d:
d = t
ans = i
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 | class Solution {
private int n;
private List<Integer>[] g;
public int closestMeetingNode(int[] edges, int node1, int node2) {
n = edges.length;
g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (int i = 0; i < n; ++i) {
if (edges[i] != -1) {
g[i].add(edges[i]);
}
}
int[] d1 = f(node1);
int[] d2 = f(node2);
int d = 1 << 30;
int ans = -1;
for (int i = 0; i < n; ++i) {
int t = Math.max(d1[i], d2[i]);
if (t < d) {
d = t;
ans = i;
}
}
return ans;
}
private int[] f(int i) {
int[] dist = new int[n];
Arrays.fill(dist, 1 << 30);
dist[i] = 0;
Deque<Integer> q = new ArrayDeque<>();
q.offer(i);
while (!q.isEmpty()) {
i = q.poll();
for (int j : g[i]) {
if (dist[j] == 1 << 30) {
dist[j] = dist[i] + 1;
q.offer(j);
}
}
}
return dist;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | class Solution {
public:
int closestMeetingNode(vector<int>& edges, int node1, int node2) {
int n = edges.size();
vector<vector<int>> g(n);
for (int i = 0; i < n; ++i) {
if (edges[i] != -1) {
g[i].push_back(edges[i]);
}
}
const int inf = 1 << 30;
using pii = pair<int, int>;
auto f = [&](int i) {
vector<int> dist(n, inf);
dist[i] = 0;
queue<int> q{{i}};
while (!q.empty()) {
i = q.front();
q.pop();
for (int j : g[i]) {
if (dist[j] == inf) {
dist[j] = dist[i] + 1;
q.push(j);
}
}
}
return dist;
};
vector<int> d1 = f(node1);
vector<int> d2 = f(node2);
int ans = -1, d = inf;
for (int i = 0; i < n; ++i) {
int t = max(d1[i], d2[i]);
if (t < d) {
d = t;
ans = i;
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | func closestMeetingNode(edges []int, node1 int, node2 int) int {
n := len(edges)
g := make([][]int, n)
for i, j := range edges {
if j != -1 {
g[i] = append(g[i], j)
}
}
const inf int = 1 << 30
f := func(i int) []int {
dist := make([]int, n)
for j := range dist {
dist[j] = inf
}
dist[i] = 0
q := []int{i}
for len(q) > 0 {
i = q[0]
q = q[1:]
for _, j := range g[i] {
if dist[j] == inf {
dist[j] = dist[i] + 1
q = append(q, j)
}
}
}
return dist
}
d1 := f(node1)
d2 := f(node2)
ans, d := -1, inf
for i, a := range d1 {
b := d2[i]
t := max(a, b)
if t < d {
d = t
ans = i
}
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 | function closestMeetingNode(edges: number[], node1: number, node2: number): number {
const n = edges.length;
const g = Array.from({ length: n }, () => []);
for (let i = 0; i < n; ++i) {
if (edges[i] != -1) {
g[i].push(edges[i]);
}
}
const inf = 1 << 30;
const f = (i: number) => {
const dist = new Array(n).fill(inf);
dist[i] = 0;
const q: number[] = [i];
while (q.length) {
i = q.shift();
for (const j of g[i]) {
if (dist[j] == inf) {
dist[j] = dist[i] + 1;
q.push(j);
}
}
}
return dist;
};
const d1 = f(node1);
const d2 = f(node2);
let ans = -1;
let d = inf;
for (let i = 0; i < n; ++i) {
const t = Math.max(d1[i], d2[i]);
if (t < d) {
d = t;
ans = i;
}
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 | use std::collections::VecDeque;
impl Solution {
pub fn closest_meeting_node(edges: Vec<i32>, node1: i32, node2: i32) -> i32 {
let n = edges.len();
let mut g = vec![Vec::new(); n];
for i in 0..n {
if edges[i] != -1 {
g[i].push(edges[i] as usize);
}
}
let inf = 1 << 30;
let f = |mut i: usize| -> Vec<i32> {
let mut dist = vec![inf; n];
dist[i] = 0;
let mut q = VecDeque::new();
q.push_back(i);
while !q.is_empty() {
i = q.pop_front().unwrap();
for &j in &g[i] {
if dist[j] == inf {
dist[j] = dist[i] + 1;
q.push_back(j);
}
}
}
dist
};
let d1 = f(node1 as usize);
let d2 = f(node2 as usize);
let mut ans = -1;
let mut d = inf;
for i in 0..n {
let t = std::cmp::max(d1[i], d2[i]);
if t < d {
d = t;
ans = i as i32;
}
}
ans
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | public class Solution {
public int ClosestMeetingNode(int[] edges, int node1, int node2) {
int n = edges.Length;
List<int>[] g = new List<int>[n];
for (int i = 0; i < n; ++i) {
g[i] = new List<int>();
if (edges[i] != -1) {
g[i].Add(edges[i]);
}
}
int inf = 1 << 30;
int[] f(int i) {
int[] dist = new int[n];
Array.Fill(dist, inf);
dist[i] = 0;
Queue<int> q = new Queue<int>();
q.Enqueue(i);
while (q.Count > 0) {
i = q.Dequeue();
foreach (int j in g[i]) {
if (dist[j] == inf) {
dist[j] = dist[i] + 1;
q.Enqueue(j);
}
}
}
return dist;
}
int[] d1 = f(node1);
int[] d2 = f(node2);
int ans = -1, d = inf;
for (int i = 0; i < n; ++i) {
int t = Math.Max(d1[i], d2[i]);
if (t < d) {
d = t;
ans = i;
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 | class Solution {
func closestMeetingNode(_ edges: [Int], _ node1: Int, _ node2: Int) -> Int {
let n = edges.count
var g = [[Int]](repeating: [], count: n)
for i in 0..<n {
if edges[i] != -1 {
g[i].append(edges[i])
}
}
let inf = 1 << 30
func f(_ i: Int) -> [Int] {
var dist = [Int](repeating: inf, count: n)
dist[i] = 0
var q = [i]
var idx = 0
while idx < q.count {
let i = q[idx]
idx += 1
for j in g[i] {
if dist[j] == inf {
dist[j] = dist[i] + 1
q.append(j)
}
}
}
return dist
}
let d1 = f(node1)
let d2 = f(node2)
var ans = -1, d = inf
for i in 0..<n {
let t = max(d1[i], d2[i])
if t < d {
d = t
ans = i
}
}
return ans
}
}
|




