


题目描述
存在一棵无向连通树,树中有编号从 0 到 n - 1 的 n 个节点, 以及 n - 1 条边。
给你一个下标从 0 开始的整数数组 nums ,长度为 n ,其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。
删除树中两条 不同 的边以形成三个连通组件。对于一种删除边方案,定义如下步骤以计算其分数:
- 分别获取三个组件 每个 组件中所有节点值的异或值。
- 最大 异或值和 最小 异或值的 差值 就是这一种删除边方案的分数。
- 例如,三个组件的节点值分别是:
[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ,最小异或值是 3 ,分数是 8 - 3 = 5 。
返回在给定树上执行任意删除边方案可能的 最小 分数。
示例 1:
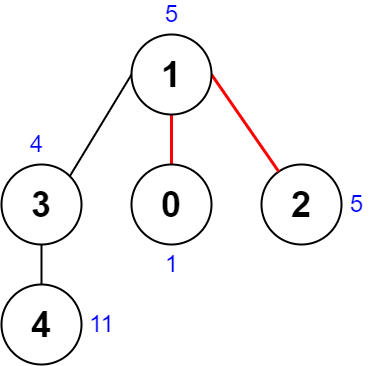
输入:nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出:9
解释:上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ,值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ,值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ,值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值,10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。
示例 2:
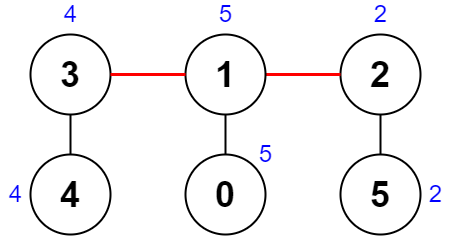
输入:nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出:0
解释:上图展示了一种删除边方案。
- 第 1 个组件的节点是 [3,4] ,值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ,值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ,值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值,0 - 0 = 0 。
无法获得比 0 更小的分数 0 。
提示:
n == nums.length3 <= n <= 10001 <= nums[i] <= 108edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges 表示一棵有效的树
解法
方法一:DFS + 子树异或和
我们记树的异或和为 \(s\),即 \(s = \text{nums}[0] \oplus \text{nums}[1] \oplus \ldots \oplus \text{nums}[n-1]\)。
接下来,枚举 \([0..n)\) 的每个点 \(i\) 作为树的根节点,将根节点与某个子节点 \(j\) 相连的边作为第一条被删除的边。这样我们就获得了两个连通块,我们记包含根节点 \(i\) 的连通块的异或和为 \(s_1\),然后我们对包含根节点 \(i\) 的连通块进行 DFS,计算出每个子树的异或和,记每次 DFS 计算出的子树异或和为 \(s_2\)。那么三个连通块的异或和分别为 \(s \oplus s_1\), \(s_2\) 和 \(s_1 \oplus s_2\)。我们需要计算这三个异或和的最大值和最小值,记为 \(\textit{mx}\) 和 \(\textit{mn}\),那么对于枚举的每一种情况,得到的分数为 \(\textit{mx} - \textit{mn}\)。求所有情况的最小值作为答案。
计算每个子树的异或和可以通过 DFS 实现。定义一个函数 \(\text{dfs}(i, fa)\),表示从节点 \(i\) 开始 DFS,而 \(fa\) 是节点 \(i\) 的父节点。函数返回值为以节点 \(i\) 为根的子树的异或和。
时间复杂度 \(O(n^2)\),空间复杂度 \(O(n)\)。其中 \(n\) 是树的节点数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | class Solution:
def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int:
def dfs(i: int, fa: int) -> int:
res = nums[i]
for j in g[i]:
if j != fa:
res ^= dfs(j, i)
return res
def dfs2(i: int, fa: int) -> int:
nonlocal s, s1, ans
res = nums[i]
for j in g[i]:
if j != fa:
s2 = dfs2(j, i)
res ^= s2
mx = max(s ^ s1, s2, s1 ^ s2)
mn = min(s ^ s1, s2, s1 ^ s2)
ans = min(ans, mx - mn)
return res
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
s = reduce(lambda x, y: x ^ y, nums)
n = len(nums)
ans = inf
for i in range(n):
for j in g[i]:
s1 = dfs(i, j)
dfs2(i, j)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53 | class Solution {
private int[] nums;
private List<Integer>[] g;
private int ans = Integer.MAX_VALUE;
private int s;
private int s1;
public int minimumScore(int[] nums, int[][] edges) {
int n = nums.length;
this.nums = nums;
g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (int[] e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
for (int x : nums) {
s ^= x;
}
for (int i = 0; i < n; ++i) {
for (int j : g[i]) {
s1 = dfs(i, j);
dfs2(i, j);
}
}
return ans;
}
private int dfs(int i, int fa) {
int res = nums[i];
for (int j : g[i]) {
if (j != fa) {
res ^= dfs(j, i);
}
}
return res;
}
private int dfs2(int i, int fa) {
int res = nums[i];
for (int j : g[i]) {
if (j != fa) {
int s2 = dfs2(j, i);
res ^= s2;
int mx = Math.max(Math.max(s ^ s1, s2), s1 ^ s2);
int mn = Math.min(Math.min(s ^ s1, s2), s1 ^ s2);
ans = Math.min(ans, mx - mn);
}
}
return res;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 | class Solution {
public:
int minimumScore(vector<int>& nums, vector<vector<int>>& edges) {
int n = nums.size();
vector<int> g[n];
for (const auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
int s = 0, s1 = 0;
int ans = INT_MAX;
for (int x : nums) {
s ^= x;
}
auto dfs = [&](this auto&& dfs, int i, int fa) -> int {
int res = nums[i];
for (int j : g[i]) {
if (j != fa) {
res ^= dfs(j, i);
}
}
return res;
};
auto dfs2 = [&](this auto&& dfs2, int i, int fa) -> int {
int res = nums[i];
for (int j : g[i]) {
if (j != fa) {
int s2 = dfs2(j, i);
res ^= s2;
int mx = max({s ^ s1, s2, s1 ^ s2});
int mn = min({s ^ s1, s2, s1 ^ s2});
ans = min(ans, mx - mn);
}
}
return res;
};
for (int i = 0; i < n; ++i) {
for (int j : g[i]) {
s1 = dfs(i, j);
dfs2(i, j);
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 | func minimumScore(nums []int, edges [][]int) int {
n := len(nums)
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
s, s1 := 0, 0
ans := math.MaxInt32
for _, x := range nums {
s ^= x
}
var dfs func(i, fa int) int
dfs = func(i, fa int) int {
res := nums[i]
for _, j := range g[i] {
if j != fa {
res ^= dfs(j, i)
}
}
return res
}
var dfs2 func(i, fa int) int
dfs2 = func(i, fa int) int {
res := nums[i]
for _, j := range g[i] {
if j != fa {
s2 := dfs2(j, i)
res ^= s2
mx := max(s^s1, s2, s1^s2)
mn := min(s^s1, s2, s1^s2)
ans = min(ans, mx-mn)
}
}
return res
}
for i := 0; i < n; i++ {
for _, j := range g[i] {
s1 = dfs(i, j)
dfs2(i, j)
}
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | function minimumScore(nums: number[], edges: number[][]): number {
const n = nums.length;
const g: number[][] = Array.from({ length: n }, () => []);
for (const [a, b] of edges) {
g[a].push(b);
g[b].push(a);
}
const s = nums.reduce((a, b) => a ^ b, 0);
let s1 = 0;
let ans = Number.MAX_SAFE_INTEGER;
function dfs(i: number, fa: number): number {
let res = nums[i];
for (const j of g[i]) {
if (j !== fa) {
res ^= dfs(j, i);
}
}
return res;
}
function dfs2(i: number, fa: number): number {
let res = nums[i];
for (const j of g[i]) {
if (j !== fa) {
const s2 = dfs2(j, i);
res ^= s2;
const mx = Math.max(s ^ s1, s2, s1 ^ s2);
const mn = Math.min(s ^ s1, s2, s1 ^ s2);
ans = Math.min(ans, mx - mn);
}
}
return res;
}
for (let i = 0; i < n; ++i) {
for (const j of g[i]) {
s1 = dfs(i, j);
dfs2(i, j);
}
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 | impl Solution {
pub fn minimum_score(nums: Vec<i32>, edges: Vec<Vec<i32>>) -> i32 {
let n = nums.len();
let mut g = vec![vec![]; n];
for e in edges.iter() {
let a = e[0] as usize;
let b = e[1] as usize;
g[a].push(b);
g[b].push(a);
}
let mut s1 = 0;
let mut ans = i32::MAX;
let s = nums.iter().fold(0, |acc, &x| acc ^ x);
fn dfs(i: usize, fa: usize, g: &Vec<Vec<usize>>, nums: &Vec<i32>) -> i32 {
let mut res = nums[i];
for &j in &g[i] {
if j != fa {
res ^= dfs(j, i, g, nums);
}
}
res
}
fn dfs2(
i: usize,
fa: usize,
g: &Vec<Vec<usize>>,
nums: &Vec<i32>,
s: i32,
s1: i32,
ans: &mut i32
) -> i32 {
let mut res = nums[i];
for &j in &g[i] {
if j != fa {
let s2 = dfs2(j, i, g, nums, s, s1, ans);
res ^= s2;
let mx = (s ^ s1).max(s2).max(s1 ^ s2);
let mn = (s ^ s1).min(s2).min(s1 ^ s2);
*ans = (*ans).min(mx - mn);
}
}
res
}
for i in 0..n {
for &j in &g[i] {
s1 = dfs(i, j, &g, &nums);
dfs2(i, j, &g, &nums, s, s1, &mut ans);
}
}
ans
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 | public class Solution {
public int MinimumScore(int[] nums, int[][] edges) {
int n = nums.Length;
List<int>[] g = new List<int>[n];
for (int i = 0; i < n; i++) {
g[i] = new List<int>();
}
foreach (var e in edges) {
int a = e[0], b = e[1];
g[a].Add(b);
g[b].Add(a);
}
int s = 0;
foreach (int x in nums) {
s ^= x;
}
int ans = int.MaxValue;
int s1 = 0;
int Dfs(int i, int fa) {
int res = nums[i];
foreach (int j in g[i]) {
if (j != fa) {
res ^= Dfs(j, i);
}
}
return res;
}
int Dfs2(int i, int fa) {
int res = nums[i];
foreach (int j in g[i]) {
if (j != fa) {
int s2 = Dfs2(j, i);
res ^= s2;
int mx = Math.Max(Math.Max(s ^ s1, s2), s1 ^ s2);
int mn = Math.Min(Math.Min(s ^ s1, s2), s1 ^ s2);
ans = Math.Min(ans, mx - mn);
}
}
return res;
}
for (int i = 0; i < n; ++i) {
foreach (int j in g[i]) {
s1 = Dfs(i, j);
Dfs2(i, j);
}
}
return ans;
}
}
|




