图 并查集
题目描述 Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
类型 1:只能由 Alice 遍历。 类型 2:只能由 Bob 遍历。 类型 3:Alice 和 Bob 都可以遍历。 给你一个数组 edges ,其中 edges[i] = [typei , ui , vi ] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob 都可以到达所有其他节点,则认为图是可以完全遍历的。
返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
示例 1:
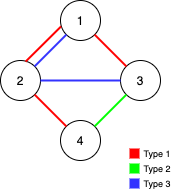
输入: n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出: 2
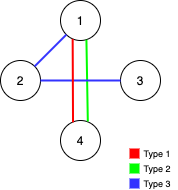
解释: 如果删除 [1,1,2] 和 [1,1,3] 这两条边,Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。
示例 2:
输入: n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出: 0
解释: 注意,删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。
示例 3:
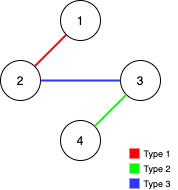
输入: n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出: -1
解释: 在当前图中,Alice 无法从其他节点到达节点 4 。类似地,Bob 也不能达到节点 1 。因此,图无法完全遍历。
提示:
1 <= n <= 10^51 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)edges[i].length == 31 <= edges[i][0] <= 31 <= edges[i][1] < edges[i][2] <= n所有元组 (typei , ui , vi ) 互不相同 解法 方法一:贪心 + 并查集 题目要求我们删除最多数目的边,使得 Alice 和 Bob 都可以遍历整个图。也即是说,我们需要保留尽可能少的边,并且要求这些边能够使得 Alice 和 Bob 都可以遍历整个图。
我们可以用两个并查集 \(ufa\) 和 \(ufb\) 分别维护 Alice 和 Bob 的遍历情况。
接下来,我们优先遍历公共边,即 \(type=3\) 的边。对于每一条公共边的两个端点 \(u\) 和 \(v\) ,如果这两个点已经在同一个连通分量中,那么我们就可以删去这条边,因此答案加一;否则我们就将这两个点合并,即执行 \(ufa.union(u, v)\) 和 \(ufb.union(u, v)\) 。
然后,我们再遍历 Alice 独有的边,即 \(type=1\) 的边。对于每一条 Alice 独有的边的两个端点 \(u\) 和 \(v\) ,如果这两个点已经在同一个连通分量中,那么我们就可以删去这条边,答案加一;否则我们就将这两个点合并,即执行 \(ufa.union(u, v)\) 。同理,对于 Bob 独有的边,我们也可以执行相同的操作。
最后,如果 Alice 和 Bob 都可以遍历整个图,那么答案就是我们删除的边数;否则答案就是 \(-1\) 。
时间复杂度 \(O(m \times \alpha(n))\) ,空间复杂度 \(O(n)\) 。其中 \(m\) 是边数,而 \(\alpha(n)\) 是阿克曼函数的反函数。
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 class UnionFind :
def __init__ ( self , n ):
self . p = list ( range ( n ))
self . size = [ 1 ] * n
self . cnt = n
def find ( self , x ):
if self . p [ x ] != x :
self . p [ x ] = self . find ( self . p [ x ])
return self . p [ x ]
def union ( self , a , b ):
pa , pb = self . find ( a - 1 ), self . find ( b - 1 )
if pa == pb :
return False
if self . size [ pa ] > self . size [ pb ]:
self . p [ pb ] = pa
self . size [ pa ] += self . size [ pb ]
else :
self . p [ pa ] = pb
self . size [ pb ] += self . size [ pa ]
self . cnt -= 1
return True
class Solution :
def maxNumEdgesToRemove ( self , n : int , edges : List [ List [ int ]]) -> int :
ufa = UnionFind ( n )
ufb = UnionFind ( n )
ans = 0
for t , u , v in edges :
if t == 3 :
if ufa . union ( u , v ):
ufb . union ( u , v )
else :
ans += 1
for t , u , v in edges :
if t == 1 :
ans += not ufa . union ( u , v )
if t == 2 :
ans += not ufb . union ( u , v )
return ans if ufa . cnt == 1 and ufb . cnt == 1 else - 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66 class UnionFind {
private int [] p ;
private int [] size ;
public int cnt ;
public UnionFind ( int n ) {
p = new int [ n ] ;
size = new int [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
p [ i ] = i ;
size [ i ] = 1 ;
}
cnt = n ;
}
public int find ( int x ) {
if ( p [ x ] != x ) {
p [ x ] = find ( p [ x ] );
}
return p [ x ] ;
}
public boolean union ( int a , int b ) {
int pa = find ( a - 1 ), pb = find ( b - 1 );
if ( pa == pb ) {
return false ;
}
if ( size [ pa ] > size [ pb ] ) {
p [ pb ] = pa ;
size [ pa ] += size [ pb ] ;
} else {
p [ pa ] = pb ;
size [ pb ] += size [ pa ] ;
}
-- cnt ;
return true ;
}
}
class Solution {
public int maxNumEdgesToRemove ( int n , int [][] edges ) {
UnionFind ufa = new UnionFind ( n );
UnionFind ufb = new UnionFind ( n );
int ans = 0 ;
for ( var e : edges ) {
int t = e [ 0 ] , u = e [ 1 ] , v = e [ 2 ] ;
if ( t == 3 ) {
if ( ufa . union ( u , v )) {
ufb . union ( u , v );
} else {
++ ans ;
}
}
}
for ( var e : edges ) {
int t = e [ 0 ] , u = e [ 1 ] , v = e [ 2 ] ;
if ( t == 1 && ! ufa . union ( u , v )) {
++ ans ;
}
if ( t == 2 && ! ufb . union ( u , v )) {
++ ans ;
}
}
return ufa . cnt == 1 && ufb . cnt == 1 ? ans : - 1 ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62 class UnionFind {
public :
int cnt ;
UnionFind ( int n ) {
p = vector < int > ( n );
size = vector < int > ( n , 1 );
iota ( p . begin (), p . end (), 0 );
cnt = n ;
}
bool unite ( int a , int b ) {
int pa = find ( a - 1 ), pb = find ( b - 1 );
if ( pa == pb ) {
return false ;
}
if ( size [ pa ] > size [ pb ]) {
p [ pb ] = pa ;
size [ pa ] += size [ pb ];
} else {
p [ pa ] = pb ;
size [ pb ] += size [ pa ];
}
-- cnt ;
return true ;
}
int find ( int x ) {
if ( p [ x ] != x ) {
p [ x ] = find ( p [ x ]);
}
return p [ x ];
}
private :
vector < int > p , size ;
};
class Solution {
public :
int maxNumEdgesToRemove ( int n , vector < vector < int >>& edges ) {
UnionFind ufa ( n );
UnionFind ufb ( n );
int ans = 0 ;
for ( auto & e : edges ) {
int t = e [ 0 ], u = e [ 1 ], v = e [ 2 ];
if ( t == 3 ) {
if ( ufa . unite ( u , v )) {
ufb . unite ( u , v );
} else {
++ ans ;
}
}
}
for ( auto & e : edges ) {
int t = e [ 0 ], u = e [ 1 ], v = e [ 2 ];
ans += t == 1 && ! ufa . unite ( u , v );
ans += t == 2 && ! ufb . unite ( u , v );
}
return ufa . cnt == 1 && ufb . cnt == 1 ? ans : -1 ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65 type unionFind struct {
p , size [] int
cnt int
}
func newUnionFind ( n int ) * unionFind {
p := make ([] int , n )
size := make ([] int , n )
for i := range p {
p [ i ] = i
size [ i ] = 1
}
return & unionFind { p , size , n }
}
func ( uf * unionFind ) find ( x int ) int {
if uf . p [ x ] != x {
uf . p [ x ] = uf . find ( uf . p [ x ])
}
return uf . p [ x ]
}
func ( uf * unionFind ) union ( a , b int ) bool {
pa , pb := uf . find ( a - 1 ), uf . find ( b - 1 )
if pa == pb {
return false
}
if uf . size [ pa ] > uf . size [ pb ] {
uf . p [ pb ] = pa
uf . size [ pa ] += uf . size [ pb ]
} else {
uf . p [ pa ] = pb
uf . size [ pb ] += uf . size [ pa ]
}
uf . cnt --
return true
}
func maxNumEdgesToRemove ( n int , edges [][] int ) ( ans int ) {
ufa := newUnionFind ( n )
ufb := newUnionFind ( n )
for _ , e := range edges {
t , u , v := e [ 0 ], e [ 1 ], e [ 2 ]
if t == 3 {
if ufa . union ( u , v ) {
ufb . union ( u , v )
} else {
ans ++
}
}
}
for _ , e := range edges {
t , u , v := e [ 0 ], e [ 1 ], e [ 2 ]
if t == 1 && ! ufa . union ( u , v ) {
ans ++
}
if t == 2 && ! ufb . union ( u , v ) {
ans ++
}
}
if ufa . cnt == 1 && ufb . cnt == 1 {
return
}
return - 1
}
GitHub