动态规划 图
题目描述 我们有 n 座城市和 m 条双向道路 roads ,其中 roads[i] = [ai , bi ] 连接城市 ai 和城市 bi 。每个城市的名称由字符串数组 names 中给出的三个大写英文字母组成。从任意城市 x 出发,你可以到达任意城市 y ,其中 y != x (即:城市和道路形成一张无向连通图)。
给定一个字符串数组 targetPath,你需要找出图中与 targetPath 的 长度相同 且 编辑距离 最小 的路径。
你需要返回 编辑距离最小的路径中节点的顺序 。该路径应当与 targetPath 的长度相等,且路径需有效(即: ans[i] 和 ans[i + 1] 间应存在直接连通的道路)。如果有多个答案,返回任意一个。
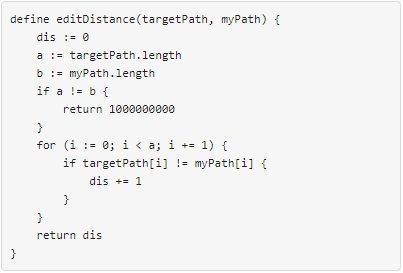
编辑距离 的定义如下:
示例 1:
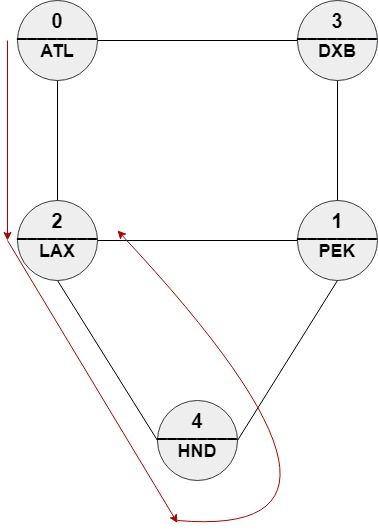
输入: n = 5, roads = [[0,2],[0,3],[1,2],[1,3],[1,4],[2,4]], names = ["ATL","PEK","LAX","DXB","HND"], targetPath = ["ATL","DXB","HND","LAX"]
输出: [0,2,4,2]
解释: [0,2,4,2], [0,3,0,2] 和 [0,3,1,2] 都是正确答案。
[0,2,4,2] 等价于 ["ATL","LAX","HND","LAX"] ,与 targetPath 的编辑距离 = 1。
[0,3,0,2] 等价于 ["ATL","DXB","ATL","LAX"] ,与 targetPath 的编辑距离 = 1。
[0,3,1,2] 等价于 ["ATL","DXB","PEK","LAX"] ,与 targetPath 的编辑距离 = 1。
示例 2:
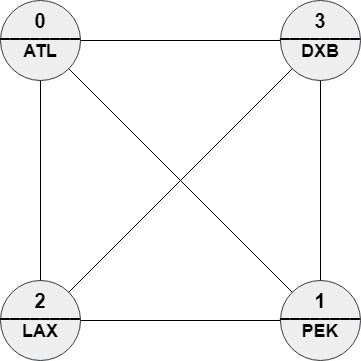
输入: n = 4, roads = [[1,0],[2,0],[3,0],[2,1],[3,1],[3,2]], names = ["ATL","PEK","LAX","DXB"], targetPath = ["ABC","DEF","GHI","JKL","MNO","PQR","STU","VWX"]
输出: [0,1,0,1,0,1,0,1]
解释: 任意路径与 targetPath 的编辑距离都等于 8。
示例 3:
输入: n = 6, roads = [[0,1],[1,2],[2,3],[3,4],[4,5]], names = ["ATL","PEK","LAX","ATL","DXB","HND"], targetPath = ["ATL","DXB","HND","DXB","ATL","LAX","PEK"]
输出: [3,4,5,4,3,2,1]
解释: [3,4,5,4,3,2,1] 是唯一与 targetPath 的编辑距离 = 0 的路径。
该路径等价于 ["ATL","DXB","HND","DXB","ATL","LAX","PEK"]
提示:
2 <= n <= 100m == roads.lengthn - 1 <= m <= (n * (n - 1) / 2)0 <= ai , bi <= n - 1ai != bi 给定的图保证是连通 的,任意两个节点至多有一个 直接连通的道路。 names.length == nnames[i].length == 3names[i] 包含大写英文字母。可能有两个名称相同 的城市。 1 <= targetPath.length <= 100targetPath[i].length == 3targetPath[i] 由大写英文字母组成。
进阶: 如果路径中每个节点只可访问一次,你该如何修改你的答案?
解法 方法一:动态规划 我们先根据给定的道路构建一个邻接表 \(g\) ,其中 \(g[i]\) 表示与城市 \(i\) 直接相连的城市列表。
然后我们定义 \(f[i][j]\) 表示 \(targetPath\) 的第 \(i\) 个城市与 \(names\) 的第 \(j\) 个城市匹配时,前 \(i\) 个城市的最小编辑距离。
那么我们可以得到状态转移方程:
\[ f[i][j] = \min_{k \in g[j]} f[i - 1][k] + (targetPath[i] \neq names[j]) \]
在状态转移的过程中,我们记录下每个状态的前驱城市,最后根据前驱城市数组 \(pre\) 从后往前还原出最优路径。
时间复杂度 \(O(m \times n^2)\) ,空间复杂度 \(O(m \times n)\) 。其中 \(m\) 和 \(n\) 分别是 \(targetPath\) 和 \(names\) 的长度。
Python3 Java C++ Go TypeScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 class Solution :
def mostSimilar (
self , n : int , roads : List [ List [ int ]], names : List [ str ], targetPath : List [ str ]
) -> List [ int ]:
g = [[] for _ in range ( n )]
for a , b in roads :
g [ a ] . append ( b )
g [ b ] . append ( a )
m = len ( targetPath )
f = [[ inf ] * n for _ in range ( m )]
pre = [[ - 1 ] * n for _ in range ( m )]
for j , s in enumerate ( names ):
f [ 0 ][ j ] = targetPath [ 0 ] != s
for i in range ( 1 , m ):
for j in range ( n ):
for k in g [ j ]:
if ( t := f [ i - 1 ][ k ] + ( targetPath [ i ] != names [ j ])) < f [ i ][ j ]:
f [ i ][ j ] = t
pre [ i ][ j ] = k
k = 0
mi = inf
for j in range ( n ):
if f [ - 1 ][ j ] < mi :
mi = f [ - 1 ][ j ]
k = j
ans = [ 0 ] * m
for i in range ( m - 1 , - 1 , - 1 ):
ans [ i ] = k
k = pre [ i ][ k ]
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 class Solution {
public List < Integer > mostSimilar ( int n , int [][] roads , String [] names , String [] targetPath ) {
List < Integer >[] g = new List [ n ] ;
Arrays . setAll ( g , i -> new ArrayList <> ());
for ( int [] r : roads ) {
int a = r [ 0 ] , b = r [ 1 ] ;
g [ a ] . add ( b );
g [ b ] . add ( a );
}
int m = targetPath . length ;
final int inf = 1 << 30 ;
int [][] f = new int [ m ][ n ] ;
int [][] pre = new int [ m ][ n ] ;
for ( int i = 0 ; i < m ; i ++ ) {
Arrays . fill ( f [ i ] , inf );
Arrays . fill ( pre [ i ] , - 1 );
}
for ( int j = 0 ; j < n ; ++ j ) {
f [ 0 ][ j ] = targetPath [ 0 ] . equals ( names [ j ] ) ? 0 : 1 ;
}
for ( int i = 1 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
for ( int k : g [ j ] ) {
int t = f [ i - 1 ][ k ] + ( targetPath [ i ] . equals ( names [ j ] ) ? 0 : 1 );
if ( t < f [ i ][ j ] ) {
f [ i ][ j ] = t ;
pre [ i ][ j ] = k ;
}
}
}
}
int mi = inf , k = 0 ;
for ( int j = 0 ; j < n ; ++ j ) {
if ( f [ m - 1 ][ j ] < mi ) {
mi = f [ m - 1 ][ j ] ;
k = j ;
}
}
List < Integer > ans = new ArrayList <> ();
for ( int i = m - 1 ; i >= 0 ; -- i ) {
ans . add ( k );
k = pre [ i ][ k ] ;
}
Collections . reverse ( ans );
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44 class Solution {
public :
vector < int > mostSimilar ( int n , vector < vector < int >>& roads , vector < string >& names , vector < string >& targetPath ) {
vector < int > g [ n ];
for ( auto & r : roads ) {
int a = r [ 0 ], b = r [ 1 ];
g [ a ]. push_back ( b );
g [ b ]. push_back ( a );
}
int m = targetPath . size ();
int f [ m ][ n ];
int pre [ m ][ n ];
memset ( f , 0x3f , sizeof ( f ));
memset ( pre , -1 , sizeof ( pre ));
for ( int j = 0 ; j < n ; ++ j ) {
f [ 0 ][ j ] = targetPath [ 0 ] != names [ j ];
}
for ( int i = 1 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
for ( int k : g [ j ]) {
int t = f [ i - 1 ][ k ] + ( targetPath [ i ] != names [ j ]);
if ( t < f [ i ][ j ]) {
f [ i ][ j ] = t ;
pre [ i ][ j ] = k ;
}
}
}
}
int k = 0 ;
int mi = 1 << 30 ;
for ( int j = 0 ; j < n ; ++ j ) {
if ( f [ m - 1 ][ j ] < mi ) {
mi = f [ m - 1 ][ j ];
k = j ;
}
}
vector < int > ans ( m );
for ( int i = m - 1 ; ~ i ; -- i ) {
ans [ i ] = k ;
k = pre [ i ][ k ];
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54 func mostSimilar ( n int , roads [][] int , names [] string , targetPath [] string ) [] int {
g := make ([][] int , n )
for _ , r := range roads {
a , b := r [ 0 ], r [ 1 ]
g [ a ] = append ( g [ a ], b )
g [ b ] = append ( g [ b ], a )
}
m := len ( targetPath )
const inf = 1 << 30
f := make ([][] int , m )
pre := make ([][] int , m )
for i := range f {
f [ i ] = make ([] int , n )
pre [ i ] = make ([] int , n )
for j := range f [ i ] {
f [ i ][ j ] = inf
pre [ i ][ j ] = - 1
}
}
for j , s := range names {
if targetPath [ 0 ] != s {
f [ 0 ][ j ] = 1
} else {
f [ 0 ][ j ] = 0
}
}
for i := 1 ; i < m ; i ++ {
for j := 0 ; j < n ; j ++ {
for _ , k := range g [ j ] {
t := f [ i - 1 ][ k ]
if targetPath [ i ] != names [ j ] {
t ++
}
if t < f [ i ][ j ] {
f [ i ][ j ] = t
pre [ i ][ j ] = k
}
}
}
}
mi , k := inf , 0
for j := 0 ; j < n ; j ++ {
if f [ m - 1 ][ j ] < mi {
mi = f [ m - 1 ][ j ]
k = j
}
}
ans := make ([] int , m )
for i := m - 1 ; i >= 0 ; i -- {
ans [ i ] = k
k = pre [ i ][ k ]
}
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 function mostSimilar (
n : number ,
roads : number [][],
names : string [],
targetPath : string [],
) : number [] {
const g : number [][] = Array . from ({ length : n }, () => []);
for ( const [ a , b ] of roads ) {
g [ a ]. push ( b );
g [ b ]. push ( a );
}
const m = targetPath . length ;
const f = Array . from ({ length : m }, () => Array . from ({ length : n }, () => Infinity ));
const pre : number [][] = Array . from ({ length : m }, () => Array . from ({ length : n }, () => - 1 ));
for ( let j = 0 ; j < n ; ++ j ) {
f [ 0 ][ j ] = names [ j ] === targetPath [ 0 ] ? 0 : 1 ;
}
for ( let i = 1 ; i < m ; ++ i ) {
for ( let j = 0 ; j < n ; ++ j ) {
for ( const k of g [ j ]) {
const t = f [ i - 1 ][ k ] + ( names [ j ] === targetPath [ i ] ? 0 : 1 );
if ( t < f [ i ][ j ]) {
f [ i ][ j ] = t ;
pre [ i ][ j ] = k ;
}
}
}
}
let k = 0 ;
let mi = Infinity ;
for ( let j = 0 ; j < n ; ++ j ) {
if ( f [ m - 1 ][ j ] < mi ) {
mi = f [ m - 1 ][ j ];
k = j ;
}
}
const ans : number [] = Array ( m ). fill ( 0 );
for ( let i = m - 1 ; ~ i ; -- i ) {
ans [ i ] = k ;
k = pre [ i ][ k ];
}
return ans ;
}
GitHub