跳转至

1437. 是否所有 1 都至少相隔 k 个元素

题目描述

给你一个由若干 0 和 1 组成的数组 nums 以及整数 k。如果所有 1 都至少相隔 k 个元素，则返回 true ；否则，返回 false 。

 

示例 1：

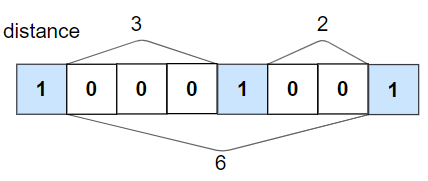
输入：nums = [1,0,0,0,1,0,0,1], k = 2
输出：true
解释：每个 1 都至少相隔 2 个元素。

示例 2：

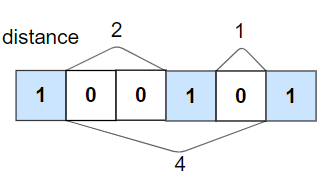
输入：nums = [1,0,0,1,0,1], k = 2
输出：false
解释：第二个 1 和第三个 1 之间只隔了 1 个元素。

 

提示：

  • 1 <= nums.length <= 105
  • 0 <= k <= nums.length
  • nums[i] 的值为 0 或 1

解法

方法一：模拟

我们可以遍历数组 \(\textit{nums}\)，用变量 \(j\) 记录上一个 \(1\) 的下标，那么当前位置 \(i\) 的元素为 \(1\) 时，只需要判断 \(i - j - 1\) 是否小于 \(k\) 即可。如果小于 \(k\)，则说明存在两个 \(1\) 之间的 \(0\) 的个数小于 \(k\)，返回 \(\text{false}\)；否则，将 \(j\) 更新为 \(i\)，继续遍历数组。

遍历结束后，返回 \(\text{true}\)。

时间复杂度 \(O(n)\)，其中 \(n\) 为数组 \(\textit{nums}\) 的长度。空间复杂度 \(O(1)\)。

1
2
3
4
5
6
7
8
9
class Solution:
    def kLengthApart(self, nums: List[int], k: int) -> bool:
        j = -inf
        for i, x in enumerate(nums):
            if x:
                if i - j - 1 < k:
                    return False
                j = i
        return True

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Solution {
    public boolean kLengthApart(int[] nums, int k) {
        int j = -(k + 1);
        for (int i = 0; i < nums.length; ++i) {
            if (nums[i] == 1) {
                if (i - j - 1 < k) {
                    return false;
                }
                j = i;
            }
        }
        return true;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
public:
    bool kLengthApart(vector<int>& nums, int k) {
        int j = -(k + 1);
        for (int i = 0; i < nums.size(); ++i) {
            if (nums[i] == 1) {
                if (i - j - 1 < k) {
                    return false;
                }
                j = i;
            }
        }
        return true;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
func kLengthApart(nums []int, k int) bool {
    j := -(k + 1)
    for i, x := range nums {
        if x == 1 {
            if i-j-1 < k {
                return false
            }
            j = i
        }
    }
    return true
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
function kLengthApart(nums: number[], k: number): boolean {
    let j = -(k + 1);
    for (let i = 0; i < nums.length; ++i) {
        if (nums[i] === 1) {
            if (i - j - 1 < k) {
                return false;
            }
            j = i;
        }
    }
    return true;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
impl Solution {
    pub fn k_length_apart(nums: Vec<i32>, k: i32) -> bool {
        let mut j = -(k + 1);
        for (i, &x) in nums.iter().enumerate() {
            if x == 1 {
                if (i as i32) - j - 1 < k {
                    return false;
                }
                j = i as i32;
            }
        }
        true
    }
}

评论