617. Merge Two Binary Trees

Description

You are given two binary trees root1 and root2.

Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.

Return the merged tree.

Note: The merging process must start from the root nodes of both trees.

 

Example 1:

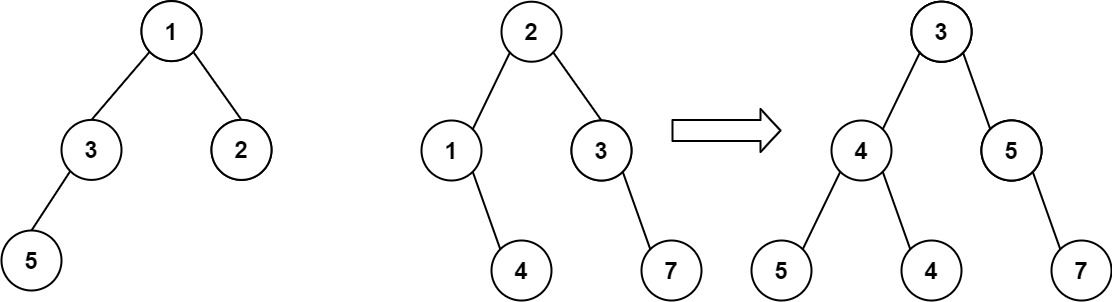
Input: root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
Output: [3,4,5,5,4,null,7]

Example 2:

Input: root1 = [1], root2 = [1,2]
Output: [2,2]

 

Constraints:

• The number of nodes in both trees is in the range [0, 2000].
• -104 <= Node.val <= 104

Solutions

Solution 1

Python3JavaC++GoTypeScriptRustJavaScript

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def mergeTrees(
        self, root1: Optional[TreeNode], root2: Optional[TreeNode]
    ) -> Optional[TreeNode]:
        if root1 is None:
            return root2
        if root2 is None:
            return root1
        node = TreeNode(root1.val + root2.val)
        node.left = self.mergeTrees(root1.left, root2.left)
        node.right = self.mergeTrees(root1.right, root2.right)
        return node

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) {
            return root2;
        }
        if (root2 == null) {
            return root1;
        }
        TreeNode node = new TreeNode(root1.val + root2.val);
        node.left = mergeTrees(root1.left, root2.left);
        node.right = mergeTrees(root1.right, root2.right);
        return node;
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (!root1) return root2;
        if (!root2) return root1;
        TreeNode* node = new TreeNode(root1->val + root2->val);
        node->left = mergeTrees(root1->left, root2->left);
        node->right = mergeTrees(root1->right, root2->right);
        return node;
    }
};

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
    if root1 == nil {
        return root2
    }
    if root2 == nil {
        return root1
    }
    node := &TreeNode{Val: root1.Val + root2.Val}
    node.Left = mergeTrees(root1.Left, root2.Left)
    node.Right = mergeTrees(root1.Right, root2.Right)
    return node
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function mergeTrees(root1: TreeNode | null, root2: TreeNode | null): TreeNode | null {
    if (root1 === null && root2 === null) return null;
    if (root1 === null) return root2;
    if (root2 === null) return root1;
    const left = mergeTrees(root1.left, root2.left);
    const right = mergeTrees(root1.right, root2.right);
    return new TreeNode(root1.val + root2.val, left, right);
}

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    pub fn merge_trees(
        root1: Option<Rc<RefCell<TreeNode>>>,
        root2: Option<Rc<RefCell<TreeNode>>>,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        match (root1.is_some(), root2.is_some()) {
            (false, false) => None,
            (true, false) => root1,
            (false, true) => root2,
            (true, true) => {
                {
                    let mut r1 = root1.as_ref().unwrap().borrow_mut();
                    let mut r2 = root2.as_ref().unwrap().borrow_mut();
                    r1.val += r2.val;
                    r1.left = Self::merge_trees(r1.left.take(), r2.left.take());
                    r1.right = Self::merge_trees(r1.right.take(), r2.right.take());
                }
                root1
            }
        }
    }
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {TreeNode}
 */
var mergeTrees = function (root1, root2) {
    if (!root1) {
        return root2;
    }
    if (!root2) {
        return root1;
    }
    const node = new TreeNode(root1.val + root2.val);
    node.left = mergeTrees(root1.left, root2.left);
    node.right = mergeTrees(root1.right, root2.right);
    return node;
};

Comments