Skip to content

407. Trapping Rain Water II

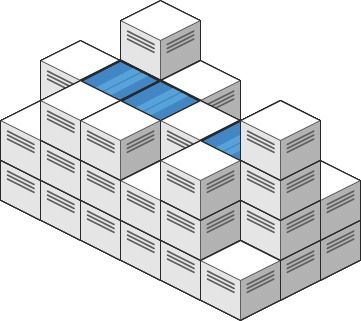
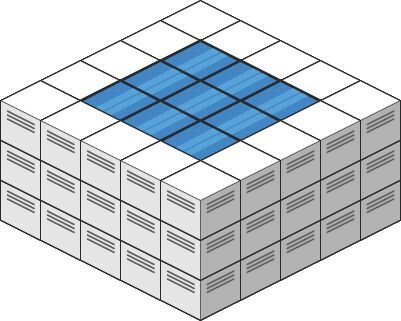
Description

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

 

Example 1:

Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.

Example 2:

Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10

 

Constraints:

  • m == heightMap.length
  • n == heightMap[i].length
  • 1 <= m, n <= 200
  • 0 <= heightMap[i][j] <= 2 * 104

Solutions

Solution 1: Priority Queue (Min Heap)

This is a variant of the trapping rain water problem. Since the heights on the matrix boundaries are fixed, we can add these boundary heights to a priority queue. Then, we repeatedly take out the minimum height from the priority queue and compare it with the heights of its four adjacent cells. If an adjacent cell's height is less than the current height, we can trap water there. The volume of trapped water is the difference between the current height and the adjacent height. We then add the larger height back to the priority queue and repeat this process until the priority queue is empty.

The time complexity is \(O(m \times n \times \log (m \times n))\), and the space complexity is \(O(m \times n)\), where \(m\) and \(n\) are the number of rows and columns in the matrix, respectively.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def trapRainWater(self, heightMap: List[List[int]]) -> int:
        m, n = len(heightMap), len(heightMap[0])
        vis = [[False] * n for _ in range(m)]
        pq = []
        for i in range(m):
            for j in range(n):
                if i == 0 or i == m - 1 or j == 0 or j == n - 1:
                    heappush(pq, (heightMap[i][j], i, j))
                    vis[i][j] = True
        ans = 0
        dirs = (-1, 0, 1, 0, -1)
        while pq:
            h, i, j = heappop(pq)
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if x >= 0 and x < m and y >= 0 and y < n and not vis[x][y]:
                    ans += max(0, h - heightMap[x][y])
                    vis[x][y] = True
                    heappush(pq, (max(h, heightMap[x][y]), x, y))
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int trapRainWater(int[][] heightMap) {
        int m = heightMap.length, n = heightMap[0].length;
        boolean[][] vis = new boolean[m][n];
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    pq.offer(new int[] {heightMap[i][j], i, j});
                    vis[i][j] = true;
                }
            }
        }
        int ans = 0;
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!pq.isEmpty()) {
            var p = pq.poll();
            for (int k = 0; k < 4; ++k) {
                int x = p[1] + dirs[k], y = p[2] + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]) {
                    ans += Math.max(0, p[0] - heightMap[x][y]);
                    vis[x][y] = true;
                    pq.offer(new int[] {Math.max(p[0], heightMap[x][y]), x, y});
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        using tii = tuple<int, int, int>;
        priority_queue<tii, vector<tii>, greater<tii>> pq;
        int m = heightMap.size(), n = heightMap[0].size();
        bool vis[m][n];
        memset(vis, 0, sizeof vis);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    pq.emplace(heightMap[i][j], i, j);
                    vis[i][j] = true;
                }
            }
        }
        int ans = 0;
        int dirs[5] = {-1, 0, 1, 0, -1};
        while (!pq.empty()) {
            auto [h, i, j] = pq.top();
            pq.pop();
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]) {
                    ans += max(0, h - heightMap[x][y]);
                    vis[x][y] = true;
                    pq.emplace(max(heightMap[x][y], h), x, y);
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
func trapRainWater(heightMap [][]int) (ans int) {
    m, n := len(heightMap), len(heightMap[0])
    pq := hp{}
    vis := make([][]bool, m)
    for i, row := range heightMap {
        vis[i] = make([]bool, n)
        for j, v := range row {
            if i == 0 || i == m-1 || j == 0 || j == n-1 {
                heap.Push(&pq, tuple{v, i, j})
                vis[i][j] = true
            }
        }
    }
    dirs := []int{-1, 0, 1, 0, -1}
    for len(pq) > 0 {
        p := heap.Pop(&pq).(tuple)
        for k := 0; k < 4; k++ {
            x, y := p.i+dirs[k], p.j+dirs[k+1]
            if x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] {
                ans += max(0, p.v-heightMap[x][y])
                vis[x][y] = true
                heap.Push(&pq, tuple{max(p.v, heightMap[x][y]), x, y})
            }
        }
    }
    return
}

type tuple struct{ v, i, j int }
type hp []tuple

func (h hp) Len() int           { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].v < h[j].v }
func (h hp) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v any)        { *h = append(*h, v.(tuple)) }
func (h *hp) Pop() any          { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
function trapRainWater(heightMap: number[][]): number {
    const m = heightMap.length;
    const n = heightMap[0].length;
    const vis: boolean[][] = Array.from({ length: m }, () => new Array(n).fill(false));
    const pq = new MinPriorityQueue<[number, number, number]>({
        compare: (a, b) => a[0] - b[0],
    });
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (i === 0 || i === m - 1 || j === 0 || j === n - 1) {
                pq.enqueue([heightMap[i][j], i, j]);
                vis[i][j] = true;
            }
        }
    }

    let ans = 0;
    const dirs = [-1, 0, 1, 0, -1];
    while (!pq.isEmpty()) {
        const [h, i, j] = pq.dequeue();
        for (let k = 0; k < 4; ++k) {
            const x = i + dirs[k];
            const y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]) {
                ans += Math.max(0, h - heightMap[x][y]);
                vis[x][y] = true;
                pq.enqueue([Math.max(h, heightMap[x][y]), x, y]);
            }
        }
    }
    return ans;
}

Comments