3807. Minimum Cost to Repair Edges to Traverse a Graph 🔒

Description

You are given an undirected graph with n nodes labeled from 0 to n - 1. The graph consists of m edges represented by a 2D integer array edges, where edges[i] = [u_i, v_i, w_i] indicates that there is an edge between nodes u_i and v_i with a repair cost of w_i.

You are also given an integer k. Initially, all edges are damaged.

You may choose a non-negative integer money and repair all edges whose repair cost is less than or equal to money. All other edges remain damaged and cannot be used.

You want to travel from node 0 to node n - 1 using at most k edges.

Return an integer denoting the minimum amount of money required to make this possible, or return -1 if it is impossible.

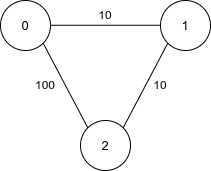
Example 1:

Input: n = 3, edges = [[0,1,10],[1,2,10],[0,2,100]], k = 1

Output: 100

Explanation:

The only valid path using at most k = 1 edge is 0 -> 2, which requires repairing the edge with cost 100. Therefore, the minimum required amount of money is 100.

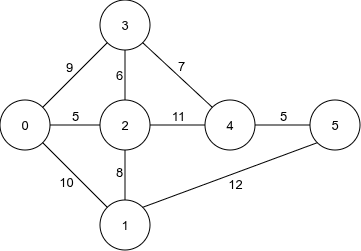
Example 2:

Input: n = 6, edges = [[0,2,5],[2,3,6],[3,4,7],[4,5,5],[0,1,10],[1,5,12],[0,3,9],[1,2,8],[2,4,11]], k = 2

Output: 12

Explanation:

With money = 12, all edges with repair cost at most 12 become usable.
This allows the path 0 -> 1 -> 5, which uses exactly 2 edges and reaches node 5.
If money < 12, there is no available path of length at most k = 2 from node 0 to node 5.
Therefore, the minimum required money is 12.

Example 3:

Input: n = 3, edges = [[0,1,1]], k = 1

Output: -1

Explanation:

It is impossible to reach node 2 from node 0 using any amount of money. Therefore, the answer is -1.

Constraints:

2 <= n <= 5 * 10⁴
1 <= edges.length == m <= 10⁵
edges[i] = [u_i, v_i, w_i]
0 <= u_i, v_i < n
1 <= w_i <= 10⁹
1 <= k <= n
There are no self-loops or duplicate edges in the graph.

Solutions

Solution 1: Binary Search + BFS

We observe that the higher the repair cost, the more edges become available, making it easier to satisfy the requirement of reaching node \(n - 1\) from node \(0\) using at most \(k\) edges. Moreover, the minimum repair cost must be among the costs in \(\textit{edges}\). Therefore, we first sort \(\textit{edges}\) by repair cost, then use binary search to find the minimum repair cost that satisfies the requirement.

We perform binary search on the index of the repair cost, defining the left boundary as \(l = 0\) and the right boundary as \(r = |\textit{edges}| - 1\). For the middle position \(mid = \lfloor (l + r) / 2 \rfloor\), we add all edges with repair cost less than or equal to \(\textit{edges}[mid][2]\) to the graph, then use BFS to determine whether we can reach node \(n - 1\) from node \(0\) using at most \(k\) edges. If possible, we update the right boundary to \(r = mid\); otherwise, we update the left boundary to \(l = mid + 1\). After the binary search completes, we need to perform one more BFS to check if \(\textit{edges}[l][2]\) satisfies the requirement. If it does, we return \(\textit{edges}[l][2]\); otherwise, we return \(-1\).

The time complexity is \(O((m + n) \times \log m)\) and the space complexity is \(O(n)\), where \(n\) and \(m\) are the number of nodes and edges, respectively.

Python3JavaC++GoTypeScript

class Solution:
    def minCost(self, n: int, edges: List[List[int]], k: int) -> int:
        def check(idx: int) -> bool:
            g = [[] for _ in range(n)]
            for u, v, _ in edges[: idx + 1]:
                g[u].append(v)
                g[v].append(u)
            q = [0]
            dist = 0
            vis = [False] * n
            vis[0] = True
            while q:
                nq = []
                for u in q:
                    if u == n - 1:
                        return dist <= k
                    for v in g[u]:
                        if not vis[v]:
                            vis[v] = True
                            nq.append(v)
                q = nq
                dist += 1
            return False

        m = len(edges)
        edges.sort(key=lambda x: x[2])
        l, r = 0, m - 1
        while l < r:
            mid = (l + r) >> 1
            if check(mid):
                r = mid
            else:
                l = mid + 1
        return edges[l][2] if check(l) else -1

class Solution {
    private int n;
    private int[][] edges;
    private int k;

    public int minCost(int n, int[][] edges, int k) {
        this.n = n;
        this.edges = edges;
        this.k = k;
        Arrays.sort(edges, (a, b) -> a[2] - b[2]);
        int l = 0, r = edges.length - 1;
        while (l < r) {
            int mid = (l + r) >> 1;
            if (check(mid)) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return check(l) ? edges[l][2] : -1;
    }

    private boolean check(int idx) {
        List<Integer>[] g = new List[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (int i = 0; i <= idx; ++i) {
            int u = edges[i][0], v = edges[i][1];
            g[u].add(v);
            g[v].add(u);
        }
        List<Integer> q = new ArrayList<>();
        q.add(0);
        int dist = 0;
        boolean[] vis = new boolean[n];
        vis[0] = true;
        while (!q.isEmpty()) {
            List<Integer> nq = new ArrayList<>();
            for (int u : q) {
                if (u == n - 1) {
                    return dist <= k;
                }
                for (int v : g[u]) {
                    if (!vis[v]) {
                        vis[v] = true;
                        nq.add(v);
                    }
                }
            }
            q = nq;
            ++dist;
        }
        return false;
    }
}

class Solution {
public:
    int minCost(int n, vector<vector<int>>& edges, int k) {
        sort(edges.begin(), edges.end(),
            [](const vector<int>& a, const vector<int>& b) {
                return a[2] < b[2];
            });

        auto check = [&](int idx) -> bool {
            vector<vector<int>> g(n);
            for (int i = 0; i <= idx; ++i) {
                int u = edges[i][0], v = edges[i][1];
                g[u].push_back(v);
                g[v].push_back(u);
            }

            vector<int> q;
            q.push_back(0);
            vector<char> vis(n, 0);
            vis[0] = 1;

            int dist = 0;
            while (!q.empty()) {
                vector<int> nq;
                for (int u : q) {
                    if (u == n - 1) {
                        return dist <= k;
                    }
                    for (int v : g[u]) {
                        if (!vis[v]) {
                            vis[v] = 1;
                            nq.push_back(v);
                        }
                    }
                }
                q.swap(nq);
                ++dist;
            }
            return false;
        };

        int m = edges.size();
        int l = 0, r = m - 1;
        while (l < r) {
            int mid = (l + r) >> 1;
            if (check(mid)) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return check(l) ? edges[l][2] : -1;
    }
};

func minCost(n int, edges [][]int, k int) int {
    sort.Slice(edges, func(i, j int) bool {
        return edges[i][2] < edges[j][2]
    })

    check := func(idx int) bool {
        g := make([][]int, n)
        for i := 0; i <= idx; i++ {
            u, v := edges[i][0], edges[i][1]
            g[u] = append(g[u], v)
            g[v] = append(g[v], u)
        }

        q := make([]int, 0, n)
        q = append(q, 0)
        vis := make([]bool, n)
        vis[0] = true

        dist := 0
        for len(q) > 0 {
            nq := make([]int, 0)
            for _, u := range q {
                if u == n-1 {
                    return dist <= k
                }
                for _, v := range g[u] {
                    if !vis[v] {
                        vis[v] = true
                        nq = append(nq, v)
                    }
                }
            }
            q = nq
            dist++
        }
        return false
    }

    m := len(edges)
    l, r := 0, m-1
    for l < r {
        mid := (l + r) >> 1
        if check(mid) {
            r = mid
        } else {
            l = mid + 1
        }
    }
    if check(l) {
        return edges[l][2]
    }
    return -1
}

function minCost(n: number, edges: number[][], k: number): number {
    edges.sort((a, b) => a[2] - b[2]);

    const check = (idx: number): boolean => {
        const g: number[][] = Array.from({ length: n }, () => []);
        for (let i = 0; i <= idx; i++) {
            const [u, v] = edges[i];
            g[u].push(v);
            g[v].push(u);
        }

        let q: number[] = [0];
        const vis: boolean[] = Array(n).fill(false);
        vis[0] = true;

        let dist = 0;
        while (q.length > 0) {
            const nq: number[] = [];
            for (const u of q) {
                if (u === n - 1) {
                    return dist <= k;
                }
                for (const v of g[u]) {
                    if (!vis[v]) {
                        vis[v] = true;
                        nq.push(v);
                    }
                }
            }
            q = nq;
            dist++;
        }
        return false;
    };

    let [l, r] = [0, edges.length - 1];
    while (l < r) {
        const mid = (l + r) >> 1;
        if (check(mid)) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    return check(l) ? edges[l][2] : -1;
}

3807. Minimum Cost to Repair Edges to Traverse a Graph 🔒

Description

Solutions

Solution 1: Binary Search + BFS

Comments