3786. Total Sum of Interaction Cost in Tree Groups
Description
You are given an integer n and an undirected tree with n nodes numbered from 0 to n - 1. This is represented by a 2D array edges of length n - 1, where edges[i] = [ui, vi] indicates an undirected edge between nodes ui and vi.
You are also given an integer array group of length n, where group[i] denotes the group label assigned to node i.
- Two nodes
uandvare considered part of the same group ifgroup[u] == group[v]. - The interaction cost between
uandvis defined as the number of edges on the unique path connecting them in the tree.
Return an integer denoting the sum of interaction costs over all unordered pairs (u, v) with u != v such that group[u] == group[v].
Example 1:
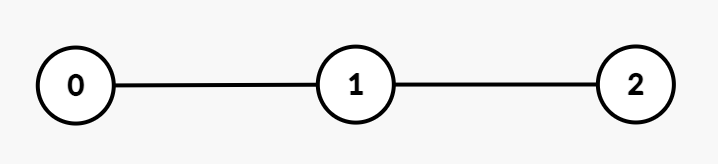
Input: n = 3, edges = [[0,1],[1,2]], group = [1,1,1]
Output: 4
Explanation:
All nodes belong to group 1. The interaction costs between the pairs of nodes are:
- Nodes
(0, 1): 1 - Nodes
(1, 2): 1 - Nodes
(0, 2): 2
Thus, the total interaction cost is 1 + 1 + 2 = 4.
Example 2:
Input: n = 3, edges = [[0,1],[1,2]], group = [3,2,3]
Output: 2
Explanation:
- Nodes 0 and 2 belong to group 3. The interaction cost between this pair is 2.
- Node 1 belongs to a different group and forms no valid pair. Therefore, the total interaction cost is 2.
Example 3:
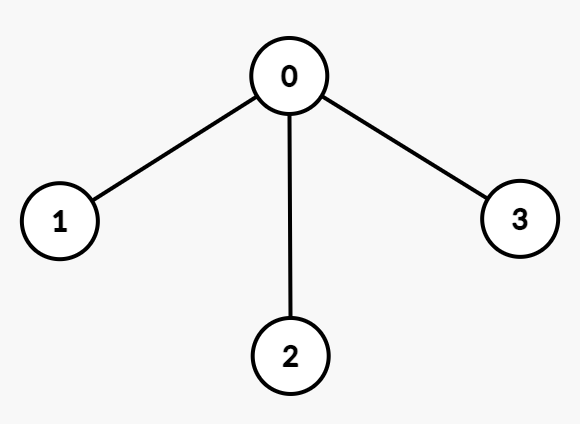
Input: n = 4, edges = [[0,1],[0,2],[0,3]], group = [1,1,4,4]
Output: 3
Explanation:
Nodes belonging to the same groups and their interaction costs are:
- Group 1: Nodes
(0, 1): 1 - Group 4: Nodes
(2, 3): 2
Thus, the total interaction cost is 1 + 2 = 3.
Example 4:
Input: n = 2, edges = [[0,1]], group = [9,8]
Output: 0
Explanation:
All nodes belong to different groups and there are no valid pairs. Therefore, the total interaction cost is 0.
Constraints:
1 <= n <= 105edges.length == n - 1edges[i] = [ui, vi]0 <= ui, vi <= n - 1group.length == n1 <= group[i] <= 20- The input is generated such that
edgesrepresents a valid tree.
Solutions
Solution 1
1 | |
1 | |
1 | |
1 | |