3615. Longest Palindromic Path in Graph
Description
You are given an integer n and an undirected graph with n nodes labeled from 0 to n - 1 and a 2D array edges, where edges[i] = [ui, vi] indicates an edge between nodes ui and vi.
You are also given a string label of length n, where label[i] is the character associated with node i.
You may start at any node and move to any adjacent node, visiting each node at most once.
Return the maximum possible length of a palindrome that can be formed by visiting a set of unique nodes along a valid path.
Example 1:
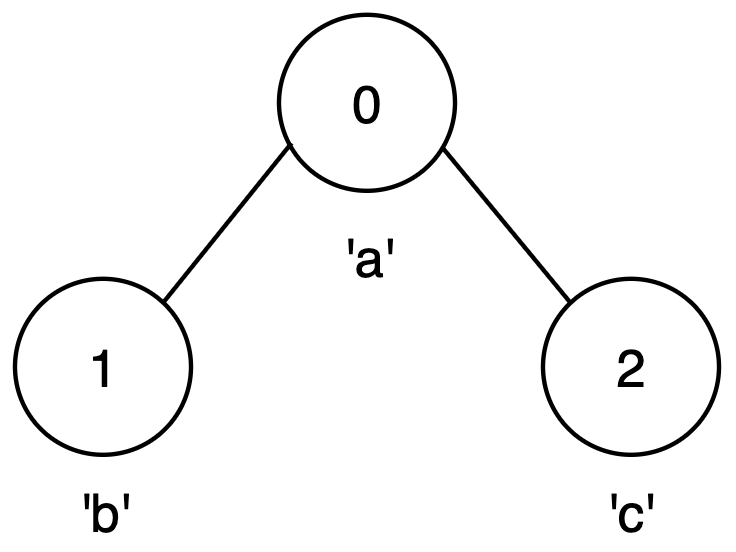
Input: n = 3, edges = [[0,1],[1,2]], label = "aba"
Output: 3
Explanation:
- The longest palindromic path is from node 0 to node 2 via node 1, following the path
0 → 1 → 2forming string"aba". - This is a valid palindrome of length 3.
Example 2:
Input: n = 3, edges = [[0,1],[0,2]], label = "abc"
Output: 1
Explanation:
- No path with more than one node forms a palindrome.
- The best option is any single node, giving a palindrome of length 1.
Example 3:
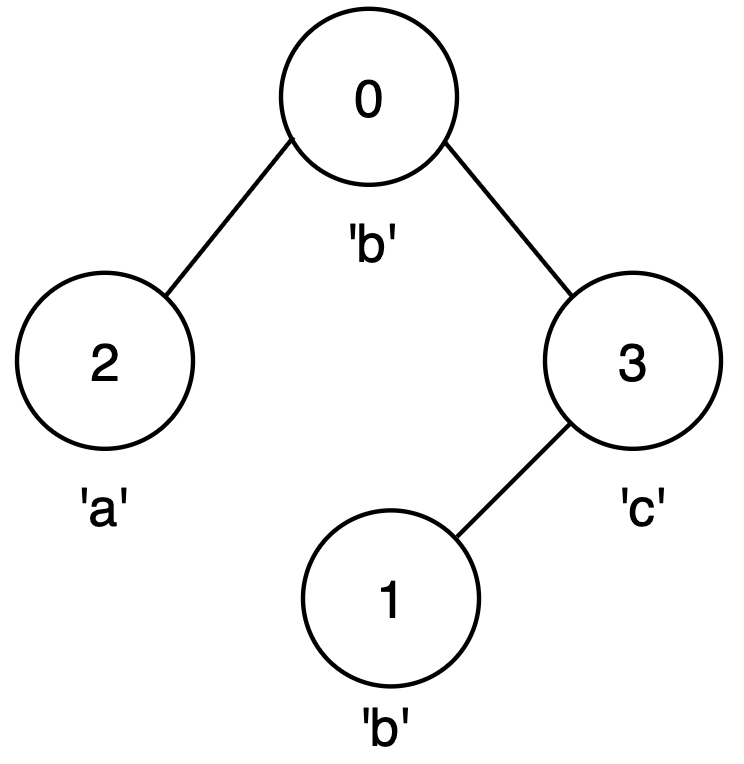
Input: n = 4, edges = [[0,2],[0,3],[3,1]], label = "bbac"
Output: 3
Explanation:
- The longest palindromic path is from node 0 to node 1, following the path
0 → 3 → 1, forming string"bcb". - This is a valid palindrome of length 3.
Constraints:
1 <= n <= 14n - 1 <= edges.length <= n * (n - 1) / 2edges[i] == [ui, vi]0 <= ui, vi <= n - 1ui != vilabel.length == nlabelconsists of lowercase English letters.- There are no duplicate edges.
Solutions
Solution 1
1 | |
1 | |
1 | |
1 | |