Skip to content

3585. Find Weighted Median Node in Tree

Description

You are given an integer n and an undirected, weighted tree rooted at node 0 with n nodes numbered from 0 to n - 1. This is represented by a 2D array edges of length n - 1, where edges[i] = [ui, vi, wi] indicates an edge from node ui to vi with weight wi.

The weighted median node is defined as the first node x on the path from ui to vi such that the sum of edge weights from ui to x is greater than or equal to half of the total path weight.

You are given a 2D integer array queries. For each queries[j] = [uj, vj], determine the weighted median node along the path from uj to vj.

Return an array ans, where ans[j] is the node index of the weighted median for queries[j].

 

Example 1:

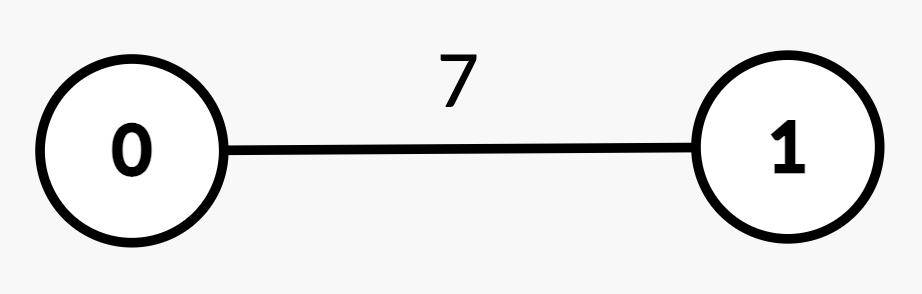
Input: n = 2, edges = [[0,1,7]], queries = [[1,0],[0,1]]

Output: [0,1]

Explanation:

Query Path Edge
Weights		 Total
Path
Weight		 Half Explanation Answer
[1, 0] 1 → 0 [7] 7 3.5 Sum from 1 → 0 = 7 >= 3.5, median is node 0. 0
[0, 1] 0 → 1 [7] 7 3.5 Sum from 0 → 1 = 7 >= 3.5, median is node 1. 1

Example 2:

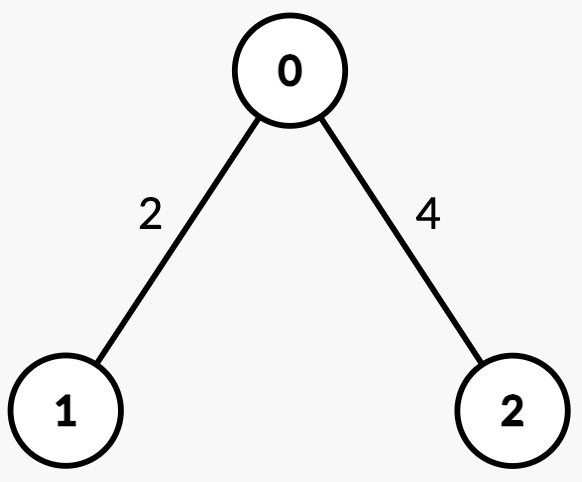
Input: n = 3, edges = [[0,1,2],[2,0,4]], queries = [[0,1],[2,0],[1,2]]

Output: [1,0,2]

Explanation:

Query Path Edge
Weights		 Total
Path
Weight		 Half Explanation Answer
[0, 1] 0 → 1 [2] 2 1 Sum from 0 → 1 = 2 >= 1, median is node 1. 1
[2, 0] 2 → 0 [4] 4 2 Sum from 2 → 0 = 4 >= 2, median is node 0. 0
[1, 2] 1 → 0 → 2 [2, 4] 6 3 Sum from 1 → 0 = 2 < 3.
Sum from 1 → 2 = 2 + 4 = 6 >= 3, median is node 2.		 2

Example 3:

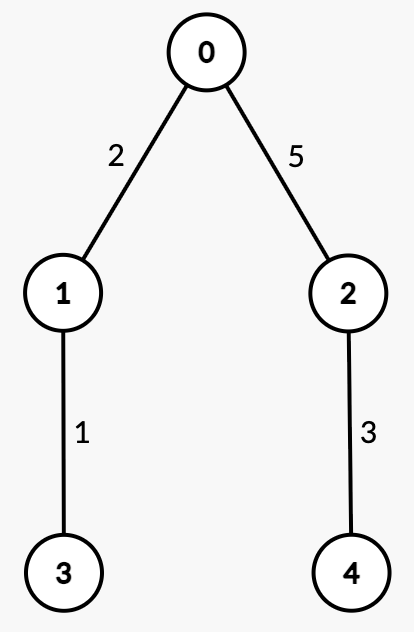
Input: n = 5, edges = [[0,1,2],[0,2,5],[1,3,1],[2,4,3]], queries = [[3,4],[1,2]]

Output: [2,2]

Explanation:

Query Path Edge
Weights		 Total
Path
Weight		 Half Explanation Answer
[3, 4] 3 → 1 → 0 → 2 → 4 [1, 2, 5, 3] 11 5.5 Sum from 3 → 1 = 1 < 5.5.
Sum from 3 → 0 = 1 + 2 = 3 < 5.5.
Sum from 3 → 2 = 1 + 2 + 5 = 8 >= 5.5, median is node 2.		 2
[1, 2] 1 → 0 → 2 [2, 5] 7 3.5

Sum from 1 → 0 = 2 < 3.5.
Sum from 1 → 2 = 2 + 5 = 7 >= 3.5, median is node 2.

 2

 

Constraints:

  • 2 <= n <= 105
  • edges.length == n - 1
  • edges[i] == [ui, vi, wi]
  • 0 <= ui, vi < n
  • 1 <= wi <= 109
  • 1 <= queries.length <= 105
  • queries[j] == [uj, vj]
  • 0 <= uj, vj < n
  • The input is generated such that edges represents a valid tree.

Solutions

Solution 1

1


1


1


1

Comments