Skip to content

2943. Maximize Area of Square Hole in Grid

Description

You are given the two integers, n and m and two integer arrays, hBars and vBars. The grid has n + 2 horizontal and m + 2 vertical bars, creating 1 x 1 unit cells. The bars are indexed starting from 1.

You can remove some of the bars in hBars from horizontal bars and some of the bars in vBars from vertical bars. Note that other bars are fixed and cannot be removed.

Return an integer denoting the maximum area of a square-shaped hole in the grid, after removing some bars (possibly none).

Β 

Example 1:

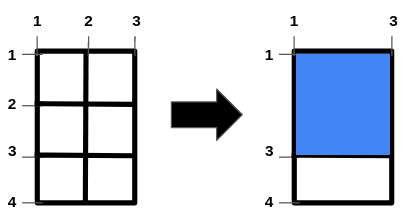
Input: n = 2, m = 1, hBars = [2,3], vBars = [2]

Output: 4

Explanation:

The left image shows the initial grid formed by the bars. The horizontal bars are [1,2,3,4], and the vertical bars areΒ [1,2,3].

One way to get the maximum square-shaped hole is by removing horizontal bar 2 and vertical bar 2.

Example 2:

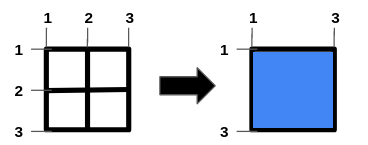
Input: n = 1, m = 1, hBars = [2], vBars = [2]

Output: 4

Explanation:

To get the maximum square-shaped hole, we remove horizontal bar 2 and vertical bar 2.

Example 3:

Input: n = 2, m = 3, hBars = [2,3], vBars = [2,4]

Output: 4

Explanation:

One way to get the maximum square-shaped hole is by removing horizontal bar 3, and vertical bar 4.

Β 

Constraints:

  • 1 <= n <= 109
  • 1 <= m <= 109
  • 1 <= hBars.length <= 100
  • 2 <= hBars[i] <= n + 1
  • 1 <= vBars.length <= 100
  • 2 <= vBars[i] <= m + 1
  • All values in hBars are distinct.
  • All values in vBars are distinct.

Solutions

Solution 1: Sorting

The problem essentially asks us to find the length of the longest consecutive increasing subsequence in the array, and then add \(1\).

We define a function \(f(\textit{nums})\) to represent the length of the longest consecutive increasing subsequence in the array \(\textit{nums}\).

For the array \(\textit{nums}\), we first sort it, then iterate through the array. If the current element \(\textit{nums}[i]\) equals the previous element \(\textit{nums}[i - 1]\) plus \(1\), it means the current element can be added to the consecutive increasing subsequence. Otherwise, the current element cannot be added to the consecutive increasing subsequence, and we need to restart counting the length of the consecutive increasing subsequence. Finally, we return the length of the consecutive increasing subsequence plus \(1\).

After finding the lengths of the longest consecutive increasing subsequences in \(\textit{hBars}\) and \(\textit{vBars}\), we take the minimum of the two as the side length of the square, and then calculate the area of the square.

The time complexity is \(O(n \times \log n)\), and the space complexity is \(O(n)\), where \(n\) is the length of the array \(\textit{hBars}\) or \(\textit{vBars}\).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution:
    def maximizeSquareHoleArea(
        self, n: int, m: int, hBars: List[int], vBars: List[int]
    ) -> int:
        def f(nums: List[int]) -> int:
            nums.sort()
            ans = cnt = 1
            for i in range(1, len(nums)):
                if nums[i] == nums[i - 1] + 1:
                    cnt += 1
                    ans = max(ans, cnt)
                else:
                    cnt = 1
            return ans + 1

        return min(f(hBars), f(vBars)) ** 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int maximizeSquareHoleArea(int n, int m, int[] hBars, int[] vBars) {
        int x = Math.min(f(hBars), f(vBars));
        return x * x;
    }

    private int f(int[] nums) {
        Arrays.sort(nums);
        int ans = 1, cnt = 1;
        for (int i = 1; i < nums.length; ++i) {
            if (nums[i] == nums[i - 1] + 1) {
                ans = Math.max(ans, ++cnt);
            } else {
                cnt = 1;
            }
        }
        return ans + 1;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maximizeSquareHoleArea(int n, int m, vector<int>& hBars, vector<int>& vBars) {
        auto f = [](vector<int>& nums) {
            int ans = 1, cnt = 1;
            sort(nums.begin(), nums.end());
            for (int i = 1; i < nums.size(); ++i) {
                if (nums[i] == nums[i - 1] + 1) {
                    ans = max(ans, ++cnt);
                } else {
                    cnt = 1;
                }
            }
            return ans + 1;
        };
        int x = min(f(hBars), f(vBars));
        return x * x;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
func maximizeSquareHoleArea(n int, m int, hBars []int, vBars []int) int {
    f := func(nums []int) int {
        sort.Ints(nums)
        ans, cnt := 1, 1
        for i, x := range nums[1:] {
            if x == nums[i]+1 {
                cnt++
                ans = max(ans, cnt)
            } else {
                cnt = 1
            }
        }
        return ans + 1
    }
    x := min(f(hBars), f(vBars))
    return x * x
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
function maximizeSquareHoleArea(n: number, m: number, hBars: number[], vBars: number[]): number {
    const f = (nums: number[]): number => {
        nums.sort((a, b) => a - b);
        let [ans, cnt] = [1, 1];
        for (let i = 1; i < nums.length; ++i) {
            if (nums[i] === nums[i - 1] + 1) {
                ans = Math.max(ans, ++cnt);
            } else {
                cnt = 1;
            }
        }
        return ans + 1;
    };
    return Math.min(f(hBars), f(vBars)) ** 2;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
impl Solution {
    pub fn maximize_square_hole_area(n: i32, m: i32, h_bars: Vec<i32>, v_bars: Vec<i32>) -> i32 {
        let f = |nums: &mut Vec<i32>| -> i32 {
            let mut ans = 1;
            let mut cnt = 1;
            nums.sort();
            for i in 1..nums.len() {
                if nums[i] == nums[i - 1] + 1 {
                    cnt += 1;
                    ans = ans.max(cnt);
                } else {
                    cnt = 1;
                }
            }
            ans + 1
        };

        let mut h_bars = h_bars;
        let mut v_bars = v_bars;
        let x = f(&mut h_bars).min(f(&mut v_bars));
        x * x
    }
}

Comments