2360. Longest Cycle in a Graph

Description

You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.

Return the length of the longest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node.

 

Example 1:

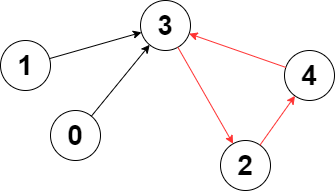
Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.

Example 2:

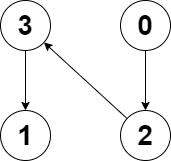
Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.

 

Constraints:

• n == edges.length
• 2 <= n <= 105
• -1 <= edges[i] < n
• edges[i] != i

Solutions

Solution 1: Traverse Starting Points

We can traverse each node in the range \([0,..,n-1]\). If a node has not been visited, we start from this node and search for adjacent nodes until we encounter a cycle or a node that has already been visited. If we encounter a cycle, we update the answer.

The time complexity is \(O(n)\) and the space complexity is \(O(n)\), where \(n\) is the number of nodes.

Similar problems:

• 2127. Maximum Employees to Be Invited to a Meeting

Python3JavaC++GoTypeScriptRust

class Solution:
    def longestCycle(self, edges: List[int]) -> int:
        n = len(edges)
        vis = [False] * n
        ans = -1
        for i in range(n):
            if vis[i]:
                continue
            j = i
            cycle = []
            while j != -1 and not vis[j]:
                vis[j] = True
                cycle.append(j)
                j = edges[j]
            if j == -1:
                continue
            m = len(cycle)
            k = next((k for k in range(m) if cycle[k] == j), inf)
            ans = max(ans, m - k)
        return ans

class Solution {
    public int longestCycle(int[] edges) {
        int n = edges.length;
        boolean[] vis = new boolean[n];
        int ans = -1;
        for (int i = 0; i < n; ++i) {
            if (vis[i]) {
                continue;
            }
            int j = i;
            List<Integer> cycle = new ArrayList<>();
            for (; j != -1 && !vis[j]; j = edges[j]) {
                vis[j] = true;
                cycle.add(j);
            }
            if (j == -1) {
                continue;
            }
            for (int k = 0; k < cycle.size(); ++k) {
                if (cycle.get(k) == j) {
                    ans = Math.max(ans, cycle.size() - k);
                    break;
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    int longestCycle(vector<int>& edges) {
        int n = edges.size();
        vector<bool> vis(n);
        int ans = -1;
        for (int i = 0; i < n; ++i) {
            if (vis[i]) {
                continue;
            }
            int j = i;
            vector<int> cycle;
            for (; j != -1 && !vis[j]; j = edges[j]) {
                vis[j] = true;
                cycle.push_back(j);
            }
            if (j == -1) {
                continue;
            }
            for (int k = 0; k < cycle.size(); ++k) {
                if (cycle[k] == j) {
                    ans = max(ans, (int) cycle.size() - k);
                    break;
                }
            }
        }
        return ans;
    }
};

func longestCycle(edges []int) int {
    vis := make([]bool, len(edges))
    ans := -1
    for i := range edges {
        if vis[i] {
            continue
        }
        j := i
        cycle := []int{}
        for ; j != -1 && !vis[j]; j = edges[j] {
            vis[j] = true
            cycle = append(cycle, j)
        }
        if j == -1 {
            continue
        }
        for k := range cycle {
            if cycle[k] == j {
                ans = max(ans, len(cycle)-k)
                break
            }
        }
    }
    return ans
}

function longestCycle(edges: number[]): number {
    const n = edges.length;
    const vis: boolean[] = Array(n).fill(false);
    let ans = -1;
    for (let i = 0; i < n; ++i) {
        if (vis[i]) {
            continue;
        }
        let j = i;
        const cycle: number[] = [];
        for (; j !== -1 && !vis[j]; j = edges[j]) {
            vis[j] = true;
            cycle.push(j);
        }
        if (j === -1) {
            continue;
        }
        for (let k = 0; k < cycle.length; ++k) {
            if (cycle[k] === j) {
                ans = Math.max(ans, cycle.length - k);
                break;
            }
        }
    }
    return ans;
}

impl Solution {
    pub fn longest_cycle(edges: Vec<i32>) -> i32 {
        let n = edges.len();
        let mut vis = vec![false; n];
        let mut ans = -1;

        for i in 0..n {
            if vis[i] {
                continue;
            }
            let mut j = i as i32;
            let mut cycle = Vec::new();

            while j != -1 && !vis[j as usize] {
                vis[j as usize] = true;
                cycle.push(j);
                j = edges[j as usize];
            }

            if j == -1 {
                continue;
            }

            for k in 0..cycle.len() {
                if cycle[k] == j {
                    ans = ans.max((cycle.len() - k) as i32);
                    break;
                }
            }
        }
        ans
    }
}

Comments