Skip to content

2313. Minimum Flips in Binary Tree to Get Result πŸ”’

Description

You are given the root of a binary tree with the following properties:

  • Leaf nodes have either the value 0 or 1, representing false and true respectively.
  • Non-leaf nodes have either the value 2, 3, 4, or 5, representing the boolean operations OR, AND, XOR, and NOT, respectively.

You are also given a boolean result, which is the desired result of the evaluation of the root node.

The evaluation of a node is as follows:

  • If the node is a leaf node, the evaluation is the value of the node, i.e. true or false.
  • Otherwise, evaluate the node's children and apply the boolean operation of its value with the children's evaluations.

In one operation, you can flip a leaf node, which causes a false node to become true, and a true node to become false.

Return the minimum number of operations that need to be performed such that the evaluation of root yields result. It can be shown that there is always a way to achieve result.

A leaf node is a node that has zero children.

Note: NOT nodes have either a left child or a right child, but other non-leaf nodes have both a left child and a right child.

 

Example 1:

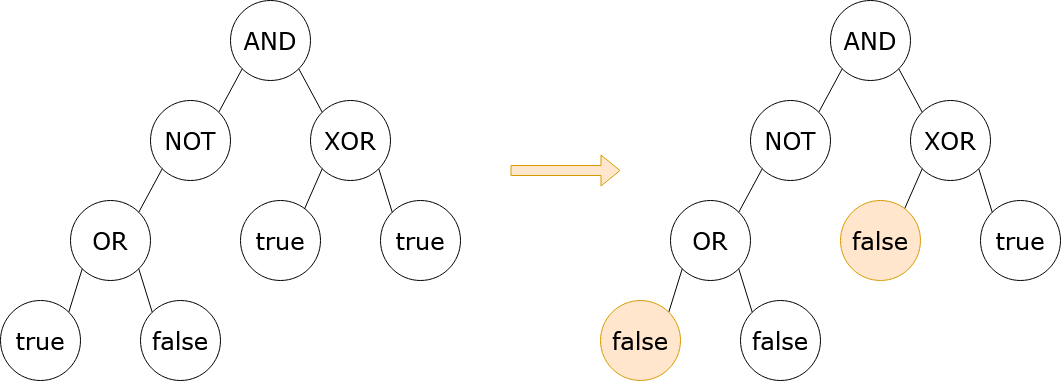
Input: root = [3,5,4,2,null,1,1,1,0], result = true
Output: 2
Explanation:
It can be shown that a minimum of 2 nodes have to be flipped to make the root of the tree
evaluate to true. One way to achieve this is shown in the diagram above.

Example 2:

Input: root = [0], result = false
Output: 0
Explanation:
The root of the tree already evaluates to false, so 0 nodes have to be flipped.

 

Constraints:

  • The number of nodes in the tree is in the range [1, 105].
  • 0 <= Node.val <= 5
  • OR, AND, and XOR nodes have 2 children.
  • NOT nodes have 1 child.
  • Leaf nodes have a value of 0 or 1.
  • Non-leaf nodes have a value of 2, 3, 4, or 5.

Solutions

Solution 1: Tree DP + Case Analysis

We define a function \(dfs(root)\), which returns an array of length 2. The first element represents the minimum number of flips needed to change the value of the \(root\) node to false, and the second element represents the minimum number of flips needed to change the value of the \(root\) node to true. The answer is \(dfs(root)[result]\).

The implementation of the function \(dfs(root)\) is as follows:

If \(root\) is null, return \([+\infty, +\infty]\).

Otherwise, let \(x\) be the value of \(root\), \(l\) be the return value of the left subtree, and \(r\) be the return value of the right subtree. Then we discuss the following cases:

  • If \(x \in \{0, 1\}\), return \([x, x \oplus 1]\).
  • If \(x = 2\), which means the boolean operator is OR, to make the value of \(root\) false, we need to make both the left and right subtrees false. Therefore, the first element of the return value is \(l[0] + r[0]\). To make the value of \(root\) true, we need at least one of the left or right subtrees to be true. Therefore, the second element of the return value is \(\min(l[0] + r[1], l[1] + r[0], l[1] + r[1])\).
  • If \(x = 3\), which means the boolean operator is AND, to make the value of \(root\) false, we need at least one of the left or right subtrees to be false. Therefore, the first element of the return value is \(\min(l[0] + r[0], l[0] + r[1], l[1] + r[0])\). To make the value of \(root\) true, we need both the left and right subtrees to be true. Therefore, the second element of the return value is \(l[1] + r[1]\).
  • If \(x = 4\), which means the boolean operator is XOR, to make the value of \(root\) false, we need both the left and right subtrees to be either false or true. Therefore, the first element of the return value is \(\min(l[0] + r[0], l[1] + r[1])\). To make the value of \(root\) true, we need the left and right subtrees to be different. Therefore, the second element of the return value is \(\min(l[0] + r[1], l[1] + r[0])\).
  • If \(x = 5\), which means the boolean operator is NOT, to make the value of \(root\) false, we need at least one of the left or right subtrees to be true. Therefore, the first element of the return value is \(\min(l[1], r[1])\). To make the value of \(root\) true, we need at least one of the left or right subtrees to be false. Therefore, the second element of the return value is \(\min(l[0], r[0])\).

The time complexity is \(O(n)\), and the space complexity is \(O(n)\). Where \(n\) is the number of nodes in the binary tree.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minimumFlips(self, root: Optional[TreeNode], result: bool) -> int:
        def dfs(root: Optional[TreeNode]) -> (int, int):
            if root is None:
                return inf, inf
            x = root.val
            if x in (0, 1):
                return x, x ^ 1
            l, r = dfs(root.left), dfs(root.right)
            if x == 2:
                return l[0] + r[0], min(l[0] + r[1], l[1] + r[0], l[1] + r[1])
            if x == 3:
                return min(l[0] + r[0], l[0] + r[1], l[1] + r[0]), l[1] + r[1]
            if x == 4:
                return min(l[0] + r[0], l[1] + r[1]), min(l[0] + r[1], l[1] + r[0])
            return min(l[1], r[1]), min(l[0], r[0])

        return dfs(root)[int(result)]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int minimumFlips(TreeNode root, boolean result) {
        return dfs(root)[result ? 1 : 0];
    }

    private int[] dfs(TreeNode root) {
        if (root == null) {
            return new int[] {1 << 30, 1 << 30};
        }
        int x = root.val;
        if (x < 2) {
            return new int[] {x, x ^ 1};
        }
        var l = dfs(root.left);
        var r = dfs(root.right);
        int a = 0, b = 0;
        if (x == 2) {
            a = l[0] + r[0];
            b = Math.min(l[0] + r[1], Math.min(l[1] + r[0], l[1] + r[1]));
        } else if (x == 3) {
            a = Math.min(l[0] + r[0], Math.min(l[0] + r[1], l[1] + r[0]));
            b = l[1] + r[1];
        } else if (x == 4) {
            a = Math.min(l[0] + r[0], l[1] + r[1]);
            b = Math.min(l[0] + r[1], l[1] + r[0]);
        } else {
            a = Math.min(l[1], r[1]);
            b = Math.min(l[0], r[0]);
        }
        return new int[] {a, b};
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minimumFlips(TreeNode* root, bool result) {
        function<pair<int, int>(TreeNode*)> dfs = [&](TreeNode* root) -> pair<int, int> {
            if (!root) {
                return {1 << 30, 1 << 30};
            }
            int x = root->val;
            if (x < 2) {
                return {x, x ^ 1};
            }
            auto [l0, l1] = dfs(root->left);
            auto [r0, r1] = dfs(root->right);
            int a = 0, b = 0;
            if (x == 2) {
                a = l0 + r0;
                b = min({l0 + r1, l1 + r0, l1 + r1});
            } else if (x == 3) {
                a = min({l0 + r0, l0 + r1, l1 + r0});
                b = l1 + r1;
            } else if (x == 4) {
                a = min(l0 + r0, l1 + r1);
                b = min(l0 + r1, l1 + r0);
            } else {
                a = min(l1, r1);
                b = min(l0, r0);
            }
            return {a, b};
        };
        auto [a, b] = dfs(root);
        return result ? b : a;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func minimumFlips(root *TreeNode, result bool) int {
    var dfs func(*TreeNode) (int, int)
    dfs = func(root *TreeNode) (int, int) {
        if root == nil {
            return 1 << 30, 1 << 30
        }
        x := root.Val
        if x < 2 {
            return x, x ^ 1
        }
        l0, l1 := dfs(root.Left)
        r0, r1 := dfs(root.Right)
        var a, b int
        if x == 2 {
            a = l0 + r0
            b = min(l0+r1, min(l1+r0, l1+r1))
        } else if x == 3 {
            a = min(l0+r0, min(l0+r1, l1+r0))
            b = l1 + r1
        } else if x == 4 {
            a = min(l0+r0, l1+r1)
            b = min(l0+r1, l1+r0)
        } else {
            a = min(l1, r1)
            b = min(l0, r0)
        }
        return a, b
    }
    a, b := dfs(root)
    if result {
        return b
    }
    return a
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function minimumFlips(root: TreeNode | null, result: boolean): number {
    const dfs = (root: TreeNode | null): [number, number] => {
        if (!root) {
            return [1 << 30, 1 << 30];
        }
        const x = root.val;
        if (x < 2) {
            return [x, x ^ 1];
        }
        const [l0, l1] = dfs(root.left);
        const [r0, r1] = dfs(root.right);
        if (x === 2) {
            return [l0 + r0, Math.min(l0 + r1, l1 + r0, l1 + r1)];
        }
        if (x === 3) {
            return [Math.min(l0 + r0, l0 + r1, l1 + r0), l1 + r1];
        }
        if (x === 4) {
            return [Math.min(l0 + r0, l1 + r1), Math.min(l0 + r1, l1 + r0)];
        }
        return [Math.min(l1, r1), Math.min(l0, r0)];
    };
    return dfs(root)[result ? 1 : 0];
}

Comments