Skip to content

2293. Min Max Game

Description

You are given a 0-indexed integer array nums whose length is a power of 2.

Apply the following algorithm on nums:

  1. Let n be the length of nums. If n == 1, end the process. Otherwise, create a new 0-indexed integer array newNums of length n / 2.
  2. For every even index i where 0 <= i < n / 2, assign the value of newNums[i] as min(nums[2 * i], nums[2 * i + 1]).
  3. For every odd index i where 0 <= i < n / 2, assign the value of newNums[i] as max(nums[2 * i], nums[2 * i + 1]).
  4. Replace the array nums with newNums.
  5. Repeat the entire process starting from step 1.

Return the last number that remains in nums after applying the algorithm.

 

Example 1:

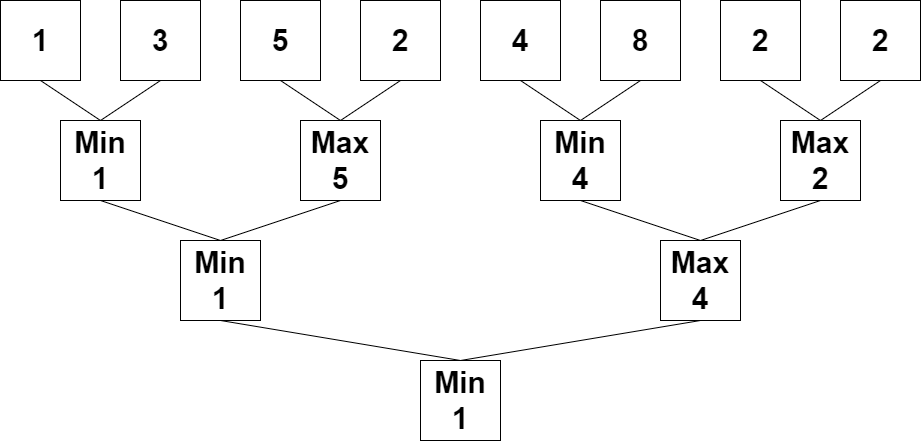
Input: nums = [1,3,5,2,4,8,2,2]
Output: 1
Explanation: The following arrays are the results of applying the algorithm repeatedly.
First: nums = [1,5,4,2]
Second: nums = [1,4]
Third: nums = [1]
1 is the last remaining number, so we return 1.

Example 2:

Input: nums = [3]
Output: 3
Explanation: 3 is already the last remaining number, so we return 3.

 

Constraints:

  • 1 <= nums.length <= 1024
  • 1 <= nums[i] <= 109
  • nums.length is a power of 2.

Solutions

Solution 1: Simulation

According to the problem statement, we can simulate the entire process, and the remaining number will be the answer. In implementation, we do not need to create an additional array; we can directly operate on the original array.

The time complexity is \(O(n)\), where \(n\) is the length of the array \(\textit{nums}\). The space complexity is \(O(1)\).

1
2
3
4
5
6
7
8
9
class Solution:
    def minMaxGame(self, nums: List[int]) -> int:
        n = len(nums)
        while n > 1:
            n >>= 1
            for i in range(n):
                a, b = nums[i << 1], nums[i << 1 | 1]
                nums[i] = min(a, b) if i % 2 == 0 else max(a, b)
        return nums[0]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
    public int minMaxGame(int[] nums) {
        for (int n = nums.length; n > 1;) {
            n >>= 1;
            for (int i = 0; i < n; ++i) {
                int a = nums[i << 1], b = nums[i << 1 | 1];
                nums[i] = i % 2 == 0 ? Math.min(a, b) : Math.max(a, b);
            }
        }
        return nums[0];
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution {
public:
    int minMaxGame(vector<int>& nums) {
        for (int n = nums.size(); n > 1;) {
            n >>= 1;
            for (int i = 0; i < n; ++i) {
                int a = nums[i << 1], b = nums[i << 1 | 1];
                nums[i] = i % 2 == 0 ? min(a, b) : max(a, b);
            }
        }
        return nums[0];
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
func minMaxGame(nums []int) int {
    for n := len(nums); n > 1; {
        n >>= 1
        for i := 0; i < n; i++ {
            a, b := nums[i<<1], nums[i<<1|1]
            if i%2 == 0 {
                nums[i] = min(a, b)
            } else {
                nums[i] = max(a, b)
            }
        }
    }
    return nums[0]
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
function minMaxGame(nums: number[]): number {
    for (let n = nums.length; n > 1; ) {
        n >>= 1;
        for (let i = 0; i < n; ++i) {
            const a = nums[i << 1];
            const b = nums[(i << 1) | 1];
            nums[i] = i % 2 == 0 ? Math.min(a, b) : Math.max(a, b);
        }
    }
    return nums[0];
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
impl Solution {
    pub fn min_max_game(mut nums: Vec<i32>) -> i32 {
        let mut n = nums.len();
        while n != 1 {
            n >>= 1;
            for i in 0..n {
                nums[i] = (if (i & 1) == 1 { i32::max } else { i32::min })(
                    nums[i << 1],
                    nums[(i << 1) | 1],
                );
            }
        }
        nums[0]
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
#define min(a, b) (((a) < (b)) ? (a) : (b))
#define max(a, b) (((a) > (b)) ? (a) : (b))

int minMaxGame(int* nums, int numsSize) {
    while (numsSize != 1) {
        numsSize >>= 1;
        for (int i = 0; i < numsSize; i++) {
            int a = nums[i << 1];
            int b = nums[i << 1 | 1];
            nums[i] = i & 1 ? max(a, b) : min(a, b);
        }
    }
    return nums[0];
}

Comments