Skip to content

2212. Maximum Points in an Archery Competition

Description

Alice and Bob are opponents in an archery competition. The competition has set the following rules:

  1. Alice first shoots numArrows arrows and then Bob shoots numArrows arrows.
  2. The points are then calculated as follows:
    1. The target has integer scoring sections ranging from 0 to 11 inclusive.
    2. For each section of the target with score k (in between 0 to 11), say Alice and Bob have shot ak and bk arrows on that section respectively. If ak >= bk, then Alice takes k points. If ak < bk, then Bob takes k points.
    3. However, if ak == bk == 0, then nobody takes k points.

  • For example, if Alice and Bob both shot 2 arrows on the section with score 11, then Alice takes 11 points. On the other hand, if Alice shot 0 arrows on the section with score 11 and Bob shot 2 arrows on that same section, then Bob takes 11 points.

You are given the integer numArrows and an integer array aliceArrows of size 12, which represents the number of arrows Alice shot on each scoring section from 0 to 11. Now, Bob wants to maximize the total number of points he can obtain.

Return the array bobArrows which represents the number of arrows Bob shot on each scoring section from 0 to 11. The sum of the values in bobArrows should equal numArrows.

If there are multiple ways for Bob to earn the maximum total points, return any one of them.

 

Example 1:

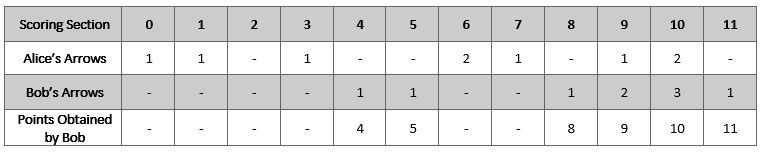
Input: numArrows = 9, aliceArrows = [1,1,0,1,0,0,2,1,0,1,2,0]
Output: [0,0,0,0,1,1,0,0,1,2,3,1]
Explanation: The table above shows how the competition is scored. 
Bob earns a total point of 4 + 5 + 8 + 9 + 10 + 11 = 47.
It can be shown that Bob cannot obtain a score higher than 47 points.

Example 2:

Input: numArrows = 3, aliceArrows = [0,0,1,0,0,0,0,0,0,0,0,2]
Output: [0,0,0,0,0,0,0,0,1,1,1,0]
Explanation: The table above shows how the competition is scored.
Bob earns a total point of 8 + 9 + 10 = 27.
It can be shown that Bob cannot obtain a score higher than 27 points.

 

Constraints:

  • 1 <= numArrows <= 105
  • aliceArrows.length == bobArrows.length == 12
  • 0 <= aliceArrows[i], bobArrows[i] <= numArrows
  • sum(aliceArrows[i]) == numArrows

Solutions

Solution 1: Binary Enumeration

Since there are only \(12\) regions, we use binary enumeration to determine in which regions \(\textit{Bob}\) scores. We use a variable \(\textit{st}\) to represent the scheme in which \(\textit{Bob}\) obtains the maximum score, and \(\textit{mx}\) to represent the maximum score \(\textit{Bob}\) obtains.

We enumerate \(\textit{Bob}\)'s scoring schemes in the range \([1, 2^m)\), where \(m\) is the length of \(\textit{aliceArrows}\). For each scheme, we calculate \(\textit{Bob}\)'s score \(\textit{s}\) and the number of arrows \(\textit{cnt}\). If \(\textit{cnt} \leq \textit{numArrows}\) and \(\textit{s} > \textit{mx}\), we update \(\textit{mx}\) and \(\textit{st}\).

Then, we calculate \(\textit{Bob}\)'s scoring scheme based on \(\textit{st}\). If there are any remaining arrows, we allocate the remaining arrows to the first region, which is the region with index \(0\).

The time complexity is \(O(2^m \times m)\), where \(m\) is the length of \(\textit{aliceArrows}\). Ignoring the space consumption of the answer array, the space complexity is \(O(1)\).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def maximumBobPoints(self, numArrows: int, aliceArrows: List[int]) -> List[int]:
        st = mx = 0
        m = len(aliceArrows)
        for mask in range(1, 1 << m):
            cnt = s = 0
            for i, x in enumerate(aliceArrows):
                if mask >> i & 1:
                    s += i
                    cnt += x + 1
            if cnt <= numArrows and s > mx:
                mx = s
                st = mask
        ans = [0] * m
        for i, x in enumerate(aliceArrows):
            if st >> i & 1:
                ans[i] = x + 1
                numArrows -= ans[i]
        ans[0] += numArrows
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int[] maximumBobPoints(int numArrows, int[] aliceArrows) {
        int st = 0, mx = 0;
        int m = aliceArrows.length;
        for (int mask = 1; mask < 1 << m; ++mask) {
            int cnt = 0, s = 0;
            for (int i = 0; i < m; ++i) {
                if ((mask >> i & 1) == 1) {
                    s += i;
                    cnt += aliceArrows[i] + 1;
                }
            }
            if (cnt <= numArrows && s > mx) {
                mx = s;
                st = mask;
            }
        }
        int[] ans = new int[m];
        for (int i = 0; i < m; ++i) {
            if ((st >> i & 1) == 1) {
                ans[i] = aliceArrows[i] + 1;
                numArrows -= ans[i];
            }
        }
        ans[0] += numArrows;
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<int> maximumBobPoints(int numArrows, vector<int>& aliceArrows) {
        int st = 0, mx = 0;
        int m = aliceArrows.size();
        for (int mask = 1; mask < 1 << m; ++mask) {
            int cnt = 0, s = 0;
            for (int i = 0; i < m; ++i) {
                if (mask >> i & 1) {
                    s += i;
                    cnt += aliceArrows[i] + 1;
                }
            }
            if (cnt <= numArrows && s > mx) {
                mx = s;
                st = mask;
            }
        }
        vector<int> ans(m);
        for (int i = 0; i < m; ++i) {
            if (st >> i & 1) {
                ans[i] = aliceArrows[i] + 1;
                numArrows -= ans[i];
            }
        }
        ans[0] += numArrows;
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func maximumBobPoints(numArrows int, aliceArrows []int) []int {
    st, mx := 0, 0
    m := len(aliceArrows)
    for mask := 1; mask < 1<<m; mask++ {
        cnt, s := 0, 0
        for i, x := range aliceArrows {
            if mask>>i&1 == 1 {
                s += i
                cnt += x + 1
            }
        }
        if cnt <= numArrows && s > mx {
            mx = s
            st = mask
        }
    }
    ans := make([]int, m)
    for i, x := range aliceArrows {
        if (st>>i)&1 == 1 {
            ans[i] = x + 1
            numArrows -= ans[i]
        }
    }
    ans[0] += numArrows
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function maximumBobPoints(numArrows: number, aliceArrows: number[]): number[] {
    let [st, mx] = [0, 0];
    const m = aliceArrows.length;
    for (let mask = 1; mask < 1 << m; mask++) {
        let [cnt, s] = [0, 0];
        for (let i = 0; i < m; i++) {
            if ((mask >> i) & 1) {
                cnt += aliceArrows[i] + 1;
                s += i;
            }
        }
        if (cnt <= numArrows && s > mx) {
            mx = s;
            st = mask;
        }
    }
    const ans: number[] = Array(m).fill(0);
    for (let i = 0; i < m; i++) {
        if ((st >> i) & 1) {
            ans[i] = aliceArrows[i] + 1;
            numArrows -= ans[i];
        }
    }
    ans[0] += numArrows;
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
impl Solution {
    pub fn maximum_bob_points(num_arrows: i32, alice_arrows: Vec<i32>) -> Vec<i32> {
        let mut st = 0;
        let mut mx = 0;
        let m = alice_arrows.len();
        for mask in 1..(1 << m) {
            let mut cnt = 0;
            let mut s = 0;
            for i in 0..m {
                if (mask >> i) & 1 == 1 {
                    s += i as i32;
                    cnt += alice_arrows[i] + 1;
                }
            }
            if cnt <= num_arrows && s > mx {
                mx = s;
                st = mask;
            }
        }
        let mut ans = vec![0; m];
        let mut num_arrows = num_arrows;
        for i in 0..m {
            if (st >> i) & 1 == 1 {
                ans[i] = alice_arrows[i] + 1;
                num_arrows -= ans[i];
            }
        }
        ans[0] += num_arrows;
        ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * @param {number} numArrows
 * @param {number[]} aliceArrows
 * @return {number[]}
 */
var maximumBobPoints = function (numArrows, aliceArrows) {
    let [st, mx] = [0, 0];
    const m = aliceArrows.length;
    for (let mask = 1; mask < 1 << m; mask++) {
        let [cnt, s] = [0, 0];
        for (let i = 0; i < m; i++) {
            if ((mask >> i) & 1) {
                cnt += aliceArrows[i] + 1;
                s += i;
            }
        }
        if (cnt <= numArrows && s > mx) {
            mx = s;
            st = mask;
        }
    }
    const ans = Array(m).fill(0);
    for (let i = 0; i < m; i++) {
        if ((st >> i) & 1) {
            ans[i] = aliceArrows[i] + 1;
            numArrows -= ans[i];
        }
    }
    ans[0] += numArrows;
    return ans;
};

Comments