2128. Remove All Ones With Row and Column Flips 🔒

Description

You are given an m x n binary matrix grid.

In one operation, you can choose any row or column and flip each value in that row or column (i.e., changing all 0's to 1's, and all 1's to 0's).

Return true if it is possible to remove all 1's from grid using any number of operations or false otherwise.

Example 1:

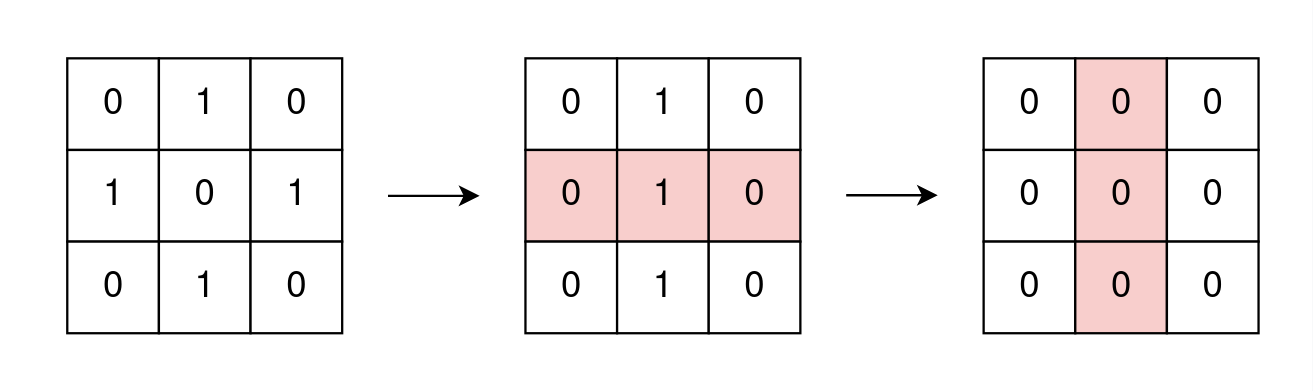
Input: grid = [[0,1,0],[1,0,1],[0,1,0]]
Output: true
Explanation: One possible way to remove all 1's from grid is to:
- Flip the middle row
- Flip the middle column

Example 2:

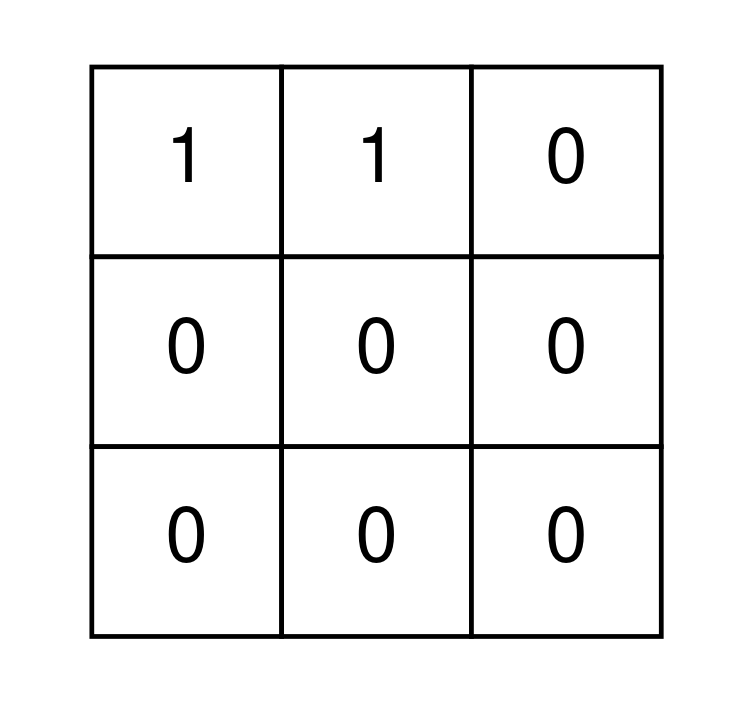
Input: grid = [[1,1,0],[0,0,0],[0,0,0]]
Output: false
Explanation: It is impossible to remove all 1's from grid.

Example 3:

Input: grid = [[0]]
Output: true
Explanation: There are no 1's in grid.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] is either 0 or 1.

Solutions

Solution 1: Hash Table

We observe that if two rows in the matrix satisfy one of the following conditions, they can be made equal by flipping certain columns:

The corresponding elements of the two rows are equal, i.e., if one row is \(1,0,0,1\), the other row is also \(1,0,0,1\);
The corresponding elements of the two rows are opposite, i.e., if one row is \(1,0,0,1\), the other row is \(0,1,1,0\).

We call two rows that satisfy one of the above conditions "equivalent rows." The answer to the problem is the maximum number of equivalent rows in the matrix.

Therefore, we can traverse each row of the matrix and convert each row into an "equivalent row" that starts with \(0\). Specifically:

If the first element of the current row is \(0\), keep the row unchanged;
If the first element of the current row is \(1\), flip every element in the row, i.e., \(0\) becomes \(1\), \(1\) becomes \(0\). In other words, we flip rows starting with \(1\) into "equivalent rows" starting with \(0\).

In this way, we only need to use a hash table to count each converted row. If the hash table contains only one element at the end, it means we can remove all \(1\)s from the matrix by flipping rows or columns.

The time complexity is \(O(mn)\) and the space complexity is \(O(m)\), where \(m\) and \(n\) are the number of rows and columns in the matrix, respectively.

Related problem:

1072. Flip Columns For Maximum Number of Equal Rows

Python3JavaC++GoTypeScriptRust

class Solution:
    def removeOnes(self, grid: List[List[int]]) -> bool:
        s = set()
        for row in grid:
            t = tuple(row) if row[0] == grid[0][0] else tuple(x ^ 1 for x in row)
            s.add(t)
        return len(s) == 1

class Solution {
    public boolean removeOnes(int[][] grid) {
        Set<String> s = new HashSet<>();
        int n = grid[0].length;
        for (var row : grid) {
            var cs = new char[n];
            for (int i = 0; i < n; ++i) {
                cs[i] = (char) (row[0] ^ row[i]);
            }
            s.add(String.valueOf(cs));
        }
        return s.size() == 1;
    }
}

class Solution {
public:
    bool removeOnes(vector<vector<int>>& grid) {
        unordered_set<string> s;
        for (auto& row : grid) {
            string t;
            for (int x : row) {
                t.push_back('0' + (row[0] == 0 ? x : x ^ 1));
            }
            s.insert(t);
        }
        return s.size() == 1;
    }
};

func removeOnes(grid [][]int) bool {
    s := map[string]bool{}
    for _, row := range grid {
        t := []byte{}
        for _, x := range row {
            if row[0] == 1 {
                x ^= 1
            }
            t = append(t, byte(x)+'0')
        }
        s[string(t)] = true
    }
    return len(s) == 1
}

function removeOnes(grid: number[][]): boolean {
    const s = new Set<string>();
    for (const row of grid) {
        if (row[0] === 1) {
            for (let i = 0; i < row.length; i++) {
                row[i] ^= 1;
            }
        }
        const t = row.join('');
        s.add(t);
    }
    return s.size === 1;
}

use std::collections::HashSet;

impl Solution {
    pub fn remove_ones(grid: Vec<Vec<i32>>) -> bool {
        let n = grid[0].len();
        let mut set = HashSet::new();

        for row in grid.iter() {
            let mut pattern = String::with_capacity(n);
            for &x in row.iter() {
                pattern.push(((row[0] ^ x) as u8 + b'0') as char);
            }
            set.insert(pattern);
        }

        set.len() == 1
    }
}

2128. Remove All Ones With Row and Column Flips 🔒

Description

Solutions

Solution 1: Hash Table

Comments