1656. Design an Ordered Stream

Description

There is a stream of n (idKey, value) pairs arriving in an arbitrary order, where idKey is an integer between 1 and n and value is a string. No two pairs have the same id.

Design a stream that returns the values in increasing order of their IDs by returning a chunk (list) of values after each insertion. The concatenation of all the chunks should result in a list of the sorted values.

Implement the OrderedStream class:

OrderedStream(int n) Constructs the stream to take n values.
String[] insert(int idKey, String value) Inserts the pair (idKey, value) into the stream, then returns the largest possible chunk of currently inserted values that appear next in the order.

Example:

Input
["OrderedStream", "insert", "insert", "insert", "insert", "insert"]
[[5], [3, "ccccc"], [1, "aaaaa"], [2, "bbbbb"], [5, "eeeee"], [4, "ddddd"]]
Output
[null, [], ["aaaaa"], ["bbbbb", "ccccc"], [], ["ddddd", "eeeee"]]

Explanation
// Note that the values ordered by ID is ["aaaaa", "bbbbb", "ccccc", "ddddd", "eeeee"].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc"); // Inserts (3, "ccccc"), returns [].
os.insert(1, "aaaaa"); // Inserts (1, "aaaaa"), returns ["aaaaa"].
os.insert(2, "bbbbb"); // Inserts (2, "bbbbb"), returns ["bbbbb", "ccccc"].
os.insert(5, "eeeee"); // Inserts (5, "eeeee"), returns [].
os.insert(4, "ddddd"); // Inserts (4, "ddddd"), returns ["ddddd", "eeeee"].
// Concatentating all the chunks returned:
// [] + ["aaaaa"] + ["bbbbb", "ccccc"] + [] + ["ddddd", "eeeee"] = ["aaaaa", "bbbbb", "ccccc", "ddddd", "eeeee"]
// The resulting order is the same as the order above.

Constraints:

1 <= n <= 1000
1 <= id <= n
value.length == 5
value consists only of lowercase letters.
Each call to insert will have a unique id.
Exactly n calls will be made to insert.

Solutions

Solution 1: Array Simulation

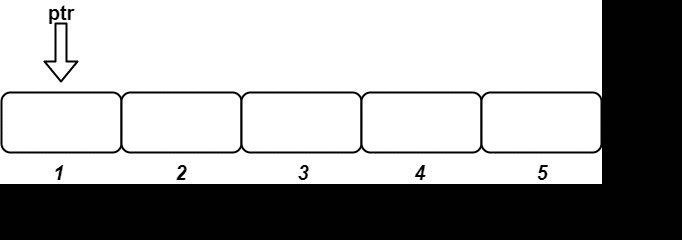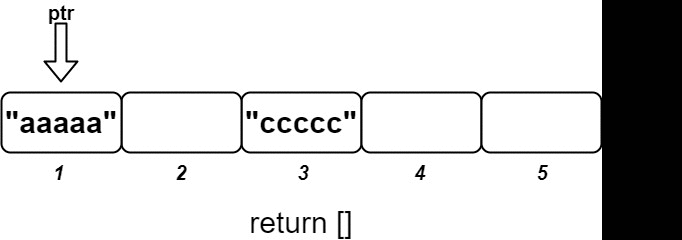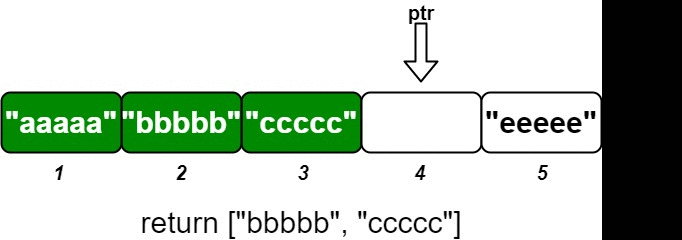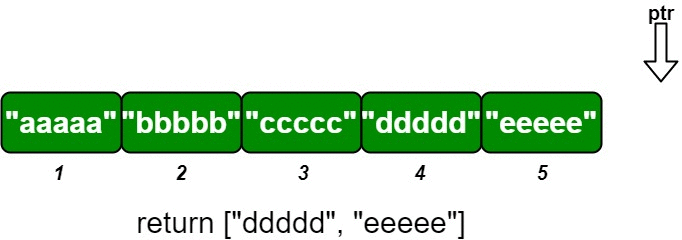
We can use an array \(\textit{data}\) of length \(n + 1\) to simulate this stream, where \(\textit{data}[i]\) represents the value of \(\textit{id} = i\). At the same time, we use a pointer \(\textit{ptr}\) to represent the current position. Initially, \(\textit{ptr} = 1\).

When inserting a new \((\textit{idKey}, \textit{value})\) pair, we update \(\textit{data}[\textit{idKey}]\) to \(\textit{value}\). Then, starting from \(\textit{ptr}\), we sequentially add \(\textit{data}[\textit{ptr}]\) to the answer until \(\textit{data}[\textit{ptr}]\) is empty.

The time complexity is \(O(n)\), and the space complexity is \(O(n)\). Where \(n\) is the length of the data stream.

Python3JavaC++GoTypeScriptRust

class OrderedStream:

    def __init__(self, n: int):
        self.ptr = 1
        self.data = [None] * (n + 1)

    def insert(self, idKey: int, value: str) -> List[str]:
        self.data[idKey] = value
        ans = []
        while self.ptr < len(self.data) and self.data[self.ptr]:
            ans.append(self.data[self.ptr])
            self.ptr += 1
        return ans


# Your OrderedStream object will be instantiated and called as such:
# obj = OrderedStream(n)
# param_1 = obj.insert(idKey,value)

class OrderedStream {
    private int ptr = 1;
    private String[] data;

    public OrderedStream(int n) {
        data = new String[n + 1];
    }

    public List<String> insert(int idKey, String value) {
        data[idKey] = value;
        List<String> ans = new ArrayList<>();
        while (ptr < data.length && data[ptr] != null) {
            ans.add(data[ptr++]);
        }
        return ans;
    }
}

/**
 * Your OrderedStream object will be instantiated and called as such:
 * OrderedStream obj = new OrderedStream(n);
 * List<String> param_1 = obj.insert(idKey,value);
 */

class OrderedStream {
public:
    OrderedStream(int n) {
        ptr = 1;
        data = vector<string>(n + 1);
    }

    vector<string> insert(int idKey, string value) {
        data[idKey] = value;
        vector<string> ans;
        while (ptr < data.size() && !data[ptr].empty()) {
            ans.push_back(data[ptr++]);
        }
        return ans;
    }

private:
    int ptr;
    vector<string> data;
};

/**
 * Your OrderedStream object will be instantiated and called as such:
 * OrderedStream* obj = new OrderedStream(n);
 * vector<string> param_1 = obj->insert(idKey,value);
 */

type OrderedStream struct {
    ptr  int
    data []string
}

func Constructor(n int) OrderedStream {
    return OrderedStream{
        ptr:  1,
        data: make([]string, n+1),
    }
}

func (this *OrderedStream) Insert(idKey int, value string) []string {
    this.data[idKey] = value
    var ans []string
    for this.ptr < len(this.data) && this.data[this.ptr] != "" {
        ans = append(ans, this.data[this.ptr])
        this.ptr++
    }
    return ans
}

/**
 * Your OrderedStream object will be instantiated and called as such:
 * obj := Constructor(n);
 * param_1 := obj.Insert(idKey,value);
 */

class OrderedStream {
    private ptr: number;
    private data: string[];

    constructor(n: number) {
        this.ptr = 1;
        this.data = Array(n + 1);
    }

    insert(idKey: number, value: string): string[] {
        this.data[idKey] = value;
        const ans: string[] = [];
        while (this.data[this.ptr]) {
            ans.push(this.data[this.ptr++]);
        }
        return ans;
    }
}

/**
 * Your OrderedStream object will be instantiated and called as such:
 * var obj = new OrderedStream(n)
 * var param_1 = obj.insert(idKey,value)
 */

struct OrderedStream {
    ptr: usize,
    data: Vec<Option<String>>,
}

impl OrderedStream {
    fn new(n: i32) -> Self {
        OrderedStream {
            ptr: 1,
            data: vec![None; (n + 1) as usize],
        }
    }

    fn insert(&mut self, id_key: i32, value: String) -> Vec<String> {
        self.data[id_key as usize] = Some(value);
        let mut ans = Vec::new();
        while self.ptr < self.data.len() && self.data[self.ptr].is_some() {
            ans.push(self.data[self.ptr].take().unwrap());
            self.ptr += 1;
        }
        ans
    }
}

1656. Design an Ordered Stream

Description

Solutions

Solution 1: Array Simulation

Comments