Skip to content

1386. Cinema Seat Allocation

Description

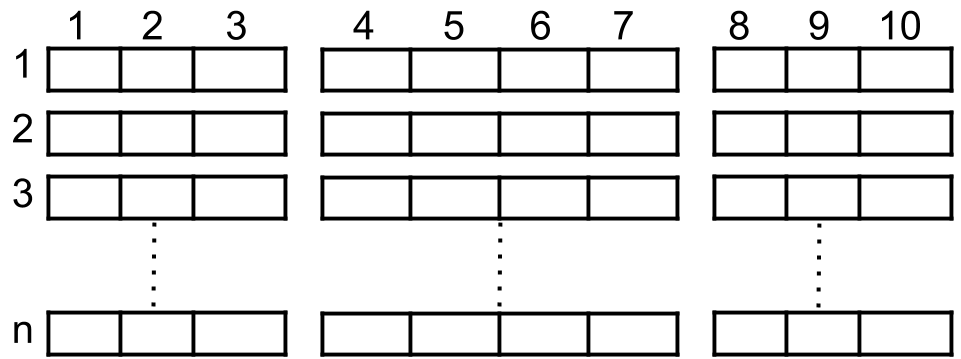
A cinemaย has nย rows of seats, numbered from 1 to nย and there are tenย seats in each row, labelled from 1ย to 10ย as shown in the figure above.

Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i] = [3,8]ย means the seat located in row 3 and labelled with 8ย is already reserved.

Return the maximum number of four-person groupsย you can assign on the cinemaย seats. A four-person groupย occupies fourย adjacent seats in one single row. Seats across an aisle (such as [3,3]ย and [3,4]) are not considered to be adjacent, but there is an exceptional caseย on which an aisle splitย a four-person group, in that case, the aisle splitย a four-person group in the middle,ย which means to have two people on each side.

ย 

Example 1:

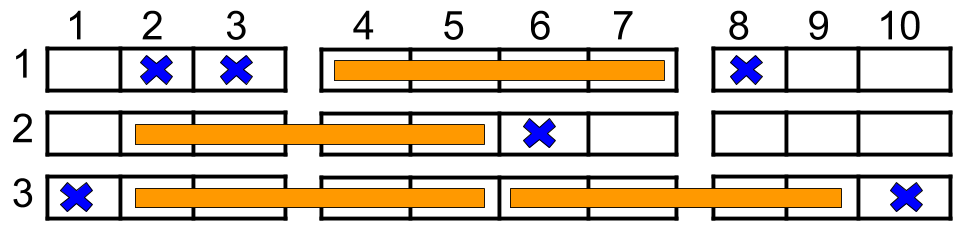
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
Explanation: The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.

Example 2:

Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2

Example 3:

Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
Output: 4

ย 

Constraints:

  • 1 <= n <= 10^9
  • 1 <=ย reservedSeats.length <= min(10*n, 10^4)
  • reservedSeats[i].length == 2
  • 1ย <=ย reservedSeats[i][0] <= n
  • 1 <=ย reservedSeats[i][1] <= 10
  • All reservedSeats[i] are distinct.

Solutions

Solution 1: Hash Table + Bit Manipulation

We use a hash table \(d\) to store all the reserved seats, where the key is the row number, and the value is the state of the reserved seats in that row, i.e., a binary number. The \(j\)-th bit being \(1\) means the \(j\)-th seat is reserved, and \(0\) means the \(j\)-th seat is not reserved.

We traverse \(reservedSeats\), for each seat \((i, j)\), we add the state of the \(j\)-th seat (corresponding to the \(10-j\) bit in the lower bits) to \(d[i]\).

For rows that do not appear in the hash table \(d\), we can arrange \(2\) families arbitrarily, so the initial answer is \((n - len(d)) \times 2\).

Next, we traverse the state of each row in the hash table. For each row, we try to arrange the situations \(1234, 5678, 3456\) in turn. If a situation can be arranged, we add \(1\) to the answer.

After the traversal, we get the final answer.

The time complexity is \(O(m)\), and the space complexity is \(O(m)\). Where \(m\) is the length of \(reservedSeats\).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution:
    def maxNumberOfFamilies(self, n: int, reservedSeats: List[List[int]]) -> int:
        d = defaultdict(int)
        for i, j in reservedSeats:
            d[i] |= 1 << (10 - j)
        masks = (0b0111100000, 0b0000011110, 0b0001111000)
        ans = (n - len(d)) * 2
        for x in d.values():
            for mask in masks:
                if (x & mask) == 0:
                    x |= mask
                    ans += 1
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int maxNumberOfFamilies(int n, int[][] reservedSeats) {
        Map<Integer, Integer> d = new HashMap<>();
        for (var e : reservedSeats) {
            int i = e[0], j = e[1];
            d.merge(i, 1 << (10 - j), (x, y) -> x | y);
        }
        int[] masks = {0b0111100000, 0b0000011110, 0b0001111000};
        int ans = (n - d.size()) * 2;
        for (int x : d.values()) {
            for (int mask : masks) {
                if ((x & mask) == 0) {
                    x |= mask;
                    ++ans;
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int maxNumberOfFamilies(int n, vector<vector<int>>& reservedSeats) {
        unordered_map<int, int> d;
        for (auto& e : reservedSeats) {
            int i = e[0], j = e[1];
            d[i] |= 1 << (10 - j);
        }
        int masks[3] = {0b0111100000, 0b0000011110, 0b0001111000};
        int ans = (n - d.size()) * 2;
        for (auto& [_, x] : d) {
            for (int& mask : masks) {
                if ((x & mask) == 0) {
                    x |= mask;
                    ++ans;
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
func maxNumberOfFamilies(n int, reservedSeats [][]int) int {
    d := map[int]int{}
    for _, e := range reservedSeats {
        i, j := e[0], e[1]
        d[i] |= 1 << (10 - j)
    }
    ans := (n - len(d)) * 2
    masks := [3]int{0b0111100000, 0b0000011110, 0b0001111000}
    for _, x := range d {
        for _, mask := range masks {
            if x&mask == 0 {
                x |= mask
                ans++
            }
        }
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
function maxNumberOfFamilies(n: number, reservedSeats: number[][]): number {
    const d: Map<number, number> = new Map();
    for (const [i, j] of reservedSeats) {
        d.set(i, (d.get(i) ?? 0) | (1 << (10 - j)));
    }
    let ans = (n - d.size) << 1;
    const masks = [0b0111100000, 0b0000011110, 0b0001111000];
    for (let [_, x] of d) {
        for (const mask of masks) {
            if ((x & mask) === 0) {
                x |= mask;
                ++ans;
            }
        }
    }
    return ans;
}

Comments