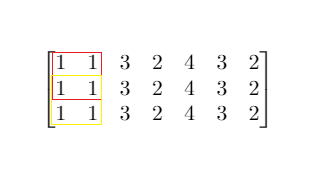Skip to content

1292. Maximum Side Length of a Square with Sum Less than or Equal to Threshold

Description

Given a m x n matrix mat and an integer threshold, return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square.

Β 

Example 1:

Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output: 2
Explanation: The maximum side length of square with sum less than 4 is 2 as shown.

Example 2:

Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output: 0

Β 

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 300
  • 0 <= mat[i][j] <= 104
  • 0 <= threshold <= 105

Solutions

We can precompute a 2D prefix sum array \(s\), where \(s[i + 1][j + 1]\) represents the sum of elements in the matrix \(mat\) from \((0, 0)\) to \((i, j)\). With this, we can calculate the sum of elements in any square region in \(O(1)\) time.

Next, we can use binary search to find the maximum side length. We enumerate the side length \(k\) of the square, and then iterate through all possible top-left positions \((i, j)\) of the square. We can calculate the sum of elements \(v\) for the square. If \(v \leq threshold\), it indicates that there exists a square region with side length \(k\) whose sum is less than or equal to the threshold; otherwise, no such square exists for the current \(k\).

The time complexity is \(O(m \times n \times \log \min(m, n))\), and the space complexity is \(O(m \times n)\).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:
        def check(k: int) -> bool:
            for i in range(m - k + 1):
                for j in range(n - k + 1):
                    v = s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j]
                    if v <= threshold:
                        return True
            return False

        m, n = len(mat), len(mat[0])
        s = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(mat, 1):
            for j, x in enumerate(row, 1):
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + x
        l, r = 0, min(m, n)
        while l < r:
            mid = (l + r + 1) >> 1
            if check(mid):
                l = mid
            else:
                r = mid - 1
        return l

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    private int m;
    private int n;
    private int threshold;
    private int[][] s;

    public int maxSideLength(int[][] mat, int threshold) {
        m = mat.length;
        n = mat[0].length;
        this.threshold = threshold;
        s = new int[m + 1][n + 1];
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
        int l = 0, r = Math.min(m, n);
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (check(mid)) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }

    private boolean check(int k) {
        for (int i = 0; i < m - k + 1; ++i) {
            for (int j = 0; j < n - k + 1; ++j) {
                if (s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j] <= threshold) {
                    return true;
                }
            }
        }
        return false;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        int m = mat.size(), n = mat[0].size();
        int s[m + 1][n + 1];
        memset(s, 0, sizeof(s));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
        auto check = [&](int k) {
            for (int i = 0; i < m - k + 1; ++i) {
                for (int j = 0; j < n - k + 1; ++j) {
                    if (s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j] <= threshold) {
                        return true;
                    }
                }
            }
            return false;
        };
        int l = 0, r = min(m, n);
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (check(mid)) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func maxSideLength(mat [][]int, threshold int) int {
    m, n := len(mat), len(mat[0])
    s := make([][]int, m+1)
    for i := range s {
        s[i] = make([]int, n+1)
    }
    for i := 1; i <= m; i++ {
        for j := 1; j <= n; j++ {
            s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + mat[i-1][j-1]
        }
    }
    check := func(k int) bool {
        for i := 0; i < m-k+1; i++ {
            for j := 0; j < n-k+1; j++ {
                if s[i+k][j+k]-s[i][j+k]-s[i+k][j]+s[i][j] <= threshold {
                    return true
                }
            }
        }
        return false
    }
    l, r := 0, min(m, n)
    for l < r {
        mid := (l + r + 1) >> 1
        if check(mid) {
            l = mid
        } else {
            r = mid - 1
        }
    }
    return l
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
function maxSideLength(mat: number[][], threshold: number): number {
    const m = mat.length;
    const n = mat[0].length;
    const s: number[][] = Array(m + 1)
        .fill(0)
        .map(() => Array(n + 1).fill(0));
    for (let i = 1; i <= m; ++i) {
        for (let j = 1; j <= n; ++j) {
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
        }
    }
    const check = (k: number): boolean => {
        for (let i = 0; i < m - k + 1; ++i) {
            for (let j = 0; j < n - k + 1; ++j) {
                if (s[i + k][j + k] - s[i + k][j] - s[i][j + k] + s[i][j] <= threshold) {
                    return true;
                }
            }
        }
        return false;
    };

    let l = 0;
    let r = Math.min(m, n);
    while (l < r) {
        const mid = (l + r + 1) >> 1;
        if (check(mid)) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }
    return l;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
impl Solution {
    pub fn max_side_length(mat: Vec<Vec<i32>>, threshold: i32) -> i32 {
        let m = mat.len();
        let n = mat[0].len();
        let mut s = vec![vec![0; n + 1]; m + 1];
        for i in 1..=m {
            for j in 1..=n {
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
        let check = |k: usize| -> bool {
            for i in 0..=m - k {
                for j in 0..=n - k {
                    if s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j] <= threshold {
                        return true;
                    }
                }
            }
            false
        };
        let mut l = 0usize;
        let mut r = m.min(n);
        while l < r {
            let mid = (l + r + 1) >> 1;
            if check(mid) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        l as i32
    }
}

Comments