Skip to content

1059. All Paths from Source Lead to Destination πŸ”’

Description

Given the edges of a directed graph where edges[i] = [ai, bi] indicates there is an edge between nodes ai and bi, and two nodes source and destination of this graph, determine whether or not all paths starting from source eventually, end at destination, that is:

  • At least one path exists from the source node to the destination node
  • If a path exists from the source node to a node with no outgoing edges, then that node is equal to destination.
  • The number of possible paths from source to destination is a finite number.

Return true if and only if all roads from source lead to destination.

 

Example 1:

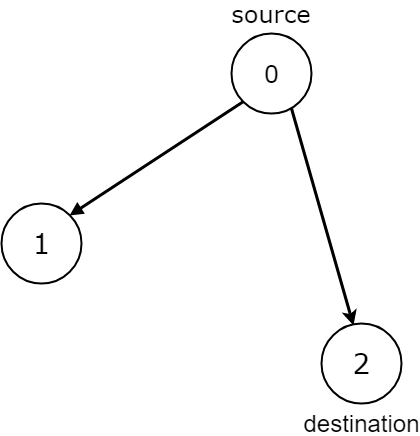
Input: n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
Output: false
Explanation: It is possible to reach and get stuck on both node 1 and node 2.

Example 2:

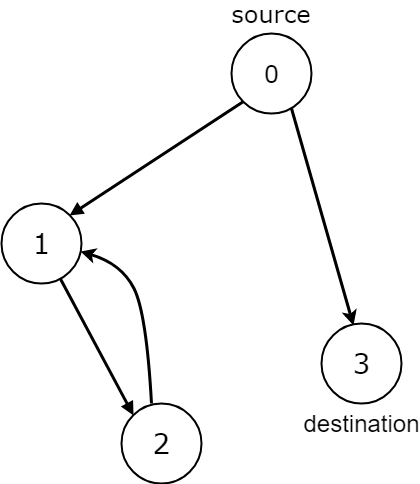
Input: n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3
Output: false
Explanation: We have two possibilities: to end at node 3, or to loop over node 1 and node 2 indefinitely.

Example 3:

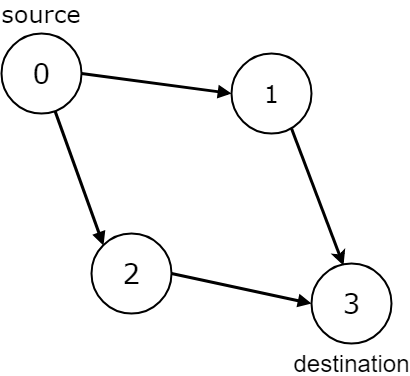
Input: n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3
Output: true

 

Constraints:

  • 1 <= n <= 104
  • 0 <= edges.length <= 104
  • edges.length == 2
  • 0 <= ai, bi <= n - 1
  • 0 <= source <= n - 1
  • 0 <= destination <= n - 1
  • The given graph may have self-loops and parallel edges.

Solutions

Solution 1: DFS

We use a state array \(\textit{state}\) to record the status of each node, where:

  • State 0 indicates the node has not been visited;
  • State 1 indicates the node is currently being visited;
  • State 2 indicates the node has been visited and can lead to the destination.

First, we build the graph as an adjacency list, then perform a depth-first search (DFS) starting from the source node. During the DFS process:

  • If the current node's state is 1, it means we have encountered a cycle, and we return \(\text{false}\) directly;
  • If the current node's state is 2, it means the node has been visited and can lead to the destination, and we return \(\text{true}\) directly;
  • If the current node has no outgoing edges, we check whether it is the destination node. If so, return \(\text{true}\); otherwise, return \(\text{false}\);
  • Otherwise, set the current node's state to 1 and recursively visit all adjacent nodes;
  • If all adjacent nodes can lead to the destination, set the current node's state to 2 and return \(\text{true}\); otherwise, return \(\text{false}\).

The answer is the result of \(\text{dfs}(\text{source})\).

The time complexity is \(O(n + m)\), where \(n\) and \(m\) are the number of nodes and edges, respectively. The space complexity is \(O(n + m)\), used to store the graph's adjacency list and state array.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def leadsToDestination(
        self, n: int, edges: List[List[int]], source: int, destination: int
    ) -> bool:
        def dfs(i: int) -> bool:
            if st[i]:
                return st[i] == 2
            if not g[i]:
                return i == destination

            st[i] = 1
            for j in g[i]:
                if not dfs(j):
                    return False
            st[i] = 2
            return True

        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
        if g[destination]:
            return False

        st = [0] * n
        return dfs(source)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    private List<Integer>[] g;
    private int[] st;
    private int destination;

    public boolean leadsToDestination(int n, int[][] edges, int source, int destination) {
        this.destination = destination;
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (int[] e : edges) {
            g[e[0]].add(e[1]);
        }
        if (!g[destination].isEmpty()) {
            return false;
        }
        st = new int[n];
        return dfs(source);
    }

    private boolean dfs(int i) {
        if (st[i] != 0) {
            return st[i] == 2;
        }
        if (g[i].isEmpty()) {
            return i == destination;
        }
        st[i] = 1;
        for (int j : g[i]) {
            if (!dfs(j)) {
                return false;
            }
        }
        st[i] = 2;
        return true;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    vector<vector<int>> g;
    vector<int> st;
    int destination;

    bool leadsToDestination(int n, vector<vector<int>>& edges, int source, int destination) {
        this->destination = destination;
        g.assign(n, {});
        for (auto& e : edges) {
            g[e[0]].push_back(e[1]);
        }
        if (!g[destination].empty()) {
            return false;
        }
        st.assign(n, 0);
        return dfs(source);
    }

    bool dfs(int i) {
        if (st[i] != 0) {
            return st[i] == 2;
        }
        if (g[i].empty()) {
            return i == destination;
        }
        st[i] = 1;
        for (int j : g[i]) {
            if (!dfs(j)) {
                return false;
            }
        }
        st[i] = 2;
        return true;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
func leadsToDestination(n int, edges [][]int, source int, destination int) bool {
    g := make([][]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], e[1])
    }
    if len(g[destination]) > 0 {
        return false
    }

    st := make([]int, n)

    var dfs func(i int) bool
    dfs = func(i int) bool {
        if st[i] != 0 {
            return st[i] == 2
        }
        if len(g[i]) == 0 {
            return i == destination
        }
        st[i] = 1
        for _, j := range g[i] {
            if !dfs(j) {
                return false
            }
        }
        st[i] = 2
        return true
    }

    return dfs(source)
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
function leadsToDestination(
    n: number,
    edges: number[][],
    source: number,
    destination: number,
): boolean {
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
    }
    if (g[destination].length > 0) {
        return false;
    }

    const st: number[] = Array(n).fill(0);

    const dfs = (i: number): boolean => {
        if (st[i] !== 0) {
            return st[i] === 2;
        }
        if (g[i].length === 0) {
            return i === destination;
        }
        st[i] = 1;
        for (const j of g[i]) {
            if (!dfs(j)) {
                return false;
            }
        }
        st[i] = 2;
        return true;
    };

    return dfs(source);
}

Comments