Skip to content

1039. Minimum Score Triangulation of Polygon

Description

You have a convex n-sided polygon where each vertex has an integer value. You are given an integer array values where values[i] is the value of the ith vertex in clockwise order.

Polygon triangulation is a process where you divide a polygon into a set of triangles and the vertices of each triangle must also be vertices of the original polygon. Note that no other shapes other than triangles are allowed in the division. This process will result in n - 2 triangles.

You will triangulate the polygon. For each triangle, the weight of that triangle is the product of the values at its vertices. The total score of the triangulation is the sum of these weights over all n - 2 triangles.

Return the minimum possible score that you can achieve with some triangulation of the polygon.

 

Example 1:

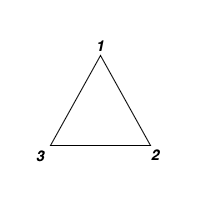
Input: values = [1,2,3]

Output: 6

Explanation: The polygon is already triangulated, and the score of the only triangle is 6.

Example 2:

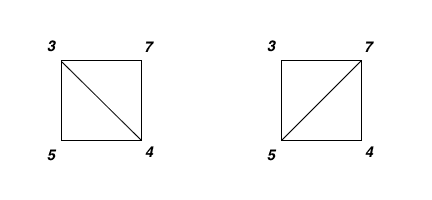
Input: values = [3,7,4,5]

Output: 144

Explanation: There are two triangulations, with possible scores: 3*7*5 + 4*5*7 = 245, or 3*4*5 + 3*4*7 = 144.
The minimum score is 144.

Example 3:

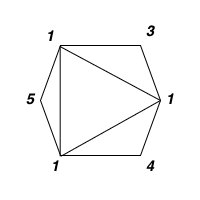
Input: values = [1,3,1,4,1,5]

Output: 13

Explanation: The minimum score triangulation is 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13.

 

Constraints:

  • n == values.length
  • 3 <= n <= 50
  • 1 <= values[i] <= 100

Solutions

Solution 1: Memoization

We design a function \(\text{dfs}(i, j)\), which represents the minimum score after triangulating the polygon from vertex \(i\) to \(j\). The answer is \(\text{dfs}(0, n - 1)\).

The calculation process of \(\text{dfs}(i, j)\) is as follows:

  • If \(i + 1 = j\), it means the polygon has only two vertices and cannot be triangulated, so we return \(0\);
  • Otherwise, we enumerate a vertex \(k\) between \(i\) and \(j\), i.e., \(i \lt k \lt j\). Triangulating the polygon from vertex \(i\) to \(j\) can be divided into two subproblems: triangulating the polygon from vertex \(i\) to \(k\) and triangulating the polygon from vertex \(k\) to \(j\). The minimum scores of these two subproblems are \(\text{dfs}(i, k)\) and \(\text{dfs}(k, j)\), respectively. The score of the triangle formed by vertices \(i\), \(j\), and \(k\) is \(\text{values}[i] \times \text{values}[k] \times \text{values}[j]\). Thus, the minimum score for this triangulation is \(\text{dfs}(i, k) + \text{dfs}(k, j) + \text{values}[i] \times \text{values}[k] \times \text{values}[j]\). We take the minimum value of all possibilities, which is the value of \(\text{dfs}(i, j)\).

To avoid repeated calculations, we can use memoization, i.e., use a hash table or an array to store the already computed function values.

Finally, we return \(\text{dfs}(0, n - 1)\).

The time complexity is \(O(n^3)\), and the space complexity is \(O(n^2)\), where \(n\) is the number of vertices in the polygon.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution:
    def minScoreTriangulation(self, values: List[int]) -> int:
        @cache
        def dfs(i: int, j: int) -> int:
            if i + 1 == j:
                return 0
            return min(
                dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]
                for k in range(i + 1, j)
            )

        return dfs(0, len(values) - 1)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    private int n;
    private int[] values;
    private Integer[][] f;

    public int minScoreTriangulation(int[] values) {
        n = values.length;
        this.values = values;
        f = new Integer[n][n];
        return dfs(0, n - 1);
    }

    private int dfs(int i, int j) {
        if (i + 1 == j) {
            return 0;
        }
        if (f[i][j] != null) {
            return f[i][j];
        }
        int ans = 1 << 30;
        for (int k = i + 1; k < j; ++k) {
            ans = Math.min(ans, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
        }
        return f[i][j] = ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int minScoreTriangulation(vector<int>& values) {
        int n = values.size();
        int f[n][n];
        memset(f, 0, sizeof(f));
        function<int(int, int)> dfs = [&](int i, int j) -> int {
            if (i + 1 == j) {
                return 0;
            }
            if (f[i][j]) {
                return f[i][j];
            }
            int ans = 1 << 30;
            for (int k = i + 1; k < j; ++k) {
                ans = min(ans, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
            }
            return f[i][j] = ans;
        };
        return dfs(0, n - 1);
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
func minScoreTriangulation(values []int) int {
    n := len(values)
    f := [50][50]int{}
    var dfs func(int, int) int
    dfs = func(i, j int) int {
        if i+1 == j {
            return 0
        }
        if f[i][j] != 0 {
            return f[i][j]
        }
        f[i][j] = 1 << 30
        for k := i + 1; k < j; k++ {
            f[i][j] = min(f[i][j], dfs(i, k)+dfs(k, j)+values[i]*values[k]*values[j])
        }
        return f[i][j]
    }
    return dfs(0, n-1)
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
function minScoreTriangulation(values: number[]): number {
    const n = values.length;
    const f: number[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => 0));
    const dfs = (i: number, j: number): number => {
        if (i + 1 === j) {
            return 0;
        }
        if (f[i][j] > 0) {
            return f[i][j];
        }
        let ans = 1 << 30;
        for (let k = i + 1; k < j; ++k) {
            ans = Math.min(ans, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
        }
        f[i][j] = ans;
        return ans;
    };
    return dfs(0, n - 1);
}

Solution 2: Dynamic Programming

We can convert the memoization approach in Solution 1 into a dynamic programming approach.

Define \(f[i][j]\) as the minimum score after triangulating the polygon from vertex \(i\) to \(j\). Initially, \(f[i][j] = 0\), and the answer is \(f[0][n-1]\).

For \(f[i][j]\) (where \(i + 1 \lt j\)), we first initialize \(f[i][j]\) to \(\infty\).

We enumerate a vertex \(k\) between \(i\) and \(j\), i.e., \(i \lt k \lt j\). Triangulating the polygon from vertex \(i\) to \(j\) can be divided into two subproblems: triangulating the polygon from vertex \(i\) to \(k\) and triangulating the polygon from vertex \(k\) to \(j\). The minimum scores of these two subproblems are \(f[i][k]\) and \(f[k][j]\), respectively. The score of the triangle formed by vertices \(i\), \(j\), and \(k\) is \(\text{values}[i] \times \text{values}[k] \times \text{values}[j]\). Thus, the minimum score for this triangulation is \(f[i][k] + f[k][j] + \text{values}[i] \times \text{values}[k] \times \text{values}[j]\). We take the minimum value of all possibilities, which becomes the value of \(f[i][j]\).

In summary, we can derive the state transition equation:

\[ f[i][j]= \begin{cases} 0, & i+1=j \\ \infty, & i+1<j \\ \min_{i<k<j} \{f[i][k]+f[k][j]+\text{values}[i] \times \text{values}[k] \times \text{values}[j]\}, & i+1<j \end{cases} \]

Note that when enumerating \(i\) and \(j\), there are two possible enumeration strategies:

  1. Enumerate \(i\) from large to small and \(j\) from small to large. This ensures that when calculating the state \(f[i][j]\), the states \(f[i][k]\) and \(f[k][j]\) have already been computed.
  2. Enumerate the interval length \(l\) from small to large, where \(3 \leq l \leq n\). Then enumerate the left endpoint \(i\) of the interval, and the right endpoint can be calculated as \(j = i + l - 1\). This also ensures that when calculating the larger interval \(f[i][j]\), the smaller intervals \(f[i][k]\) and \(f[k][j]\) have already been computed.

Finally, we return \(f[0][n-1]\).

The time complexity is \(O(n^3)\), and the space complexity is \(O(n^2)\), where \(n\) is the number of vertices in the polygon.

Related problems:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution:
    def minScoreTriangulation(self, values: List[int]) -> int:
        n = len(values)
        f = [[0] * n for _ in range(n)]
        for i in range(n - 3, -1, -1):
            for j in range(i + 2, n):
                f[i][j] = min(
                    f[i][k] + f[k][j] + values[i] * values[k] * values[j]
                    for k in range(i + 1, j)
                )
        return f[0][-1]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
    public int minScoreTriangulation(int[] values) {
        int n = values.length;
        int[][] f = new int[n][n];
        for (int i = n - 3; i >= 0; --i) {
            for (int j = i + 2; j < n; ++j) {
                f[i][j] = 1 << 30;
                for (int k = i + 1; k < j; ++k) {
                    f[i][j]
                        = Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
                }
            }
        }
        return f[0][n - 1];
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
public:
    int minScoreTriangulation(vector<int>& values) {
        int n = values.size();
        int f[n][n];
        memset(f, 0, sizeof(f));
        for (int i = n - 3; i >= 0; --i) {
            for (int j = i + 2; j < n; ++j) {
                f[i][j] = 1 << 30;
                for (int k = i + 1; k < j; ++k) {
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
                }
            }
        }
        return f[0][n - 1];
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
func minScoreTriangulation(values []int) int {
    n := len(values)
    f := [50][50]int{}
    for i := n - 3; i >= 0; i-- {
        for j := i + 2; j < n; j++ {
            f[i][j] = 1 << 30
            for k := i + 1; k < j; k++ {
                f[i][j] = min(f[i][j], f[i][k]+f[k][j]+values[i]*values[k]*values[j])
            }
        }
    }
    return f[0][n-1]
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
function minScoreTriangulation(values: number[]): number {
    const n = values.length;
    const f: number[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => 0));
    for (let i = n - 3; i >= 0; --i) {
        for (let j = i + 2; j < n; ++j) {
            f[i][j] = 1 << 30;
            for (let k = i + 1; k < j; ++k) {
                f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
            }
        }
    }
    return f[0][n - 1];
}

Solution 3: Dynamic Programming (Alternative Implementation)

In Solution 2, we mentioned two enumeration strategies. Here, we use the second strategy: enumerate the interval length \(l\) from small to large, where \(3 \leq l \leq n\). Then, enumerate the left endpoint \(i\) of the interval, and the right endpoint can be calculated as \(j = i + l - 1\).

The time complexity is \(O(n^3)\), and the space complexity is \(O(n^2)\), where \(n\) is the number of vertices in the polygon.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution:
    def minScoreTriangulation(self, values: List[int]) -> int:
        n = len(values)
        f = [[0] * n for _ in range(n)]
        for l in range(3, n + 1):
            for i in range(n - l + 1):
                j = i + l - 1
                f[i][j] = min(
                    f[i][k] + f[k][j] + values[i] * values[k] * values[j]
                    for k in range(i + 1, j)
                )
        return f[0][-1]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
    public int minScoreTriangulation(int[] values) {
        int n = values.length;
        int[][] f = new int[n][n];
        for (int l = 3; l <= n; ++l) {
            for (int i = 0; i + l - 1 < n; ++i) {
                int j = i + l - 1;
                f[i][j] = 1 << 30;
                for (int k = i + 1; k < j; ++k) {
                    f[i][j]
                        = Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
                }
            }
        }
        return f[0][n - 1];
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int minScoreTriangulation(vector<int>& values) {
        int n = values.size();
        int f[n][n];
        memset(f, 0, sizeof(f));
        for (int l = 3; l <= n; ++l) {
            for (int i = 0; i + l - 1 < n; ++i) {
                int j = i + l - 1;
                f[i][j] = 1 << 30;
                for (int k = i + 1; k < j; ++k) {
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
                }
            }
        }
        return f[0][n - 1];
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
func minScoreTriangulation(values []int) int {
    n := len(values)
    f := [50][50]int{}
    for l := 3; l <= n; l++ {
        for i := 0; i+l-1 < n; i++ {
            j := i + l - 1
            f[i][j] = 1 << 30
            for k := i + 1; k < j; k++ {
                f[i][j] = min(f[i][j], f[i][k]+f[k][j]+values[i]*values[k]*values[j])
            }
        }
    }
    return f[0][n-1]
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
function minScoreTriangulation(values: number[]): number {
    const n = values.length;
    const f: number[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => 0));
    for (let l = 3; l <= n; ++l) {
        for (let i = 0; i + l - 1 < n; ++i) {
            const j = i + l - 1;
            f[i][j] = 1 << 30;
            for (let k = i + 1; k < j; ++k) {
                f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
            }
        }
    }
    return f[0][n - 1];
}

Comments