跳转至

3643. 垂直翻转子矩阵

题目描述

给你一个 m x n 的整数矩阵 grid，以及三个整数 x、y 和 k。

整数 x 和 y 表示一个 正方形子矩阵 的左上角下标，整数 k 表示该正方形子矩阵的边长。

你的任务是垂直翻转子矩阵的行顺序。

返回更新后的矩阵。

 

示例 1：

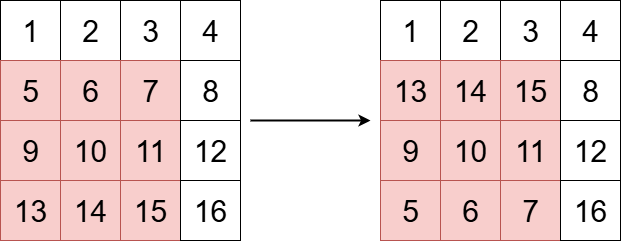
输入： grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], x = 1, y = 0, k = 3

输出： [[1,2,3,4],[13,14,15,8],[9,10,11,12],[5,6,7,16]]

解释：

上图展示了矩阵在变换前后的样子。

示例 2：

输入： grid = [[3,4,2,3],[2,3,4,2]], x = 0, y = 2, k = 2

输出： [[3,4,4,2],[2,3,2,3]]

解释：

上图展示了矩阵在变换前后的样子。

 

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 50
  • 1 <= grid[i][j] <= 100
  • 0 <= x < m
  • 0 <= y < n
  • 1 <= k <= min(m - x, n - y)

解法

方法一：模拟

我们从第 \(x\) 行开始，一共翻转 \(\lfloor \frac{k}{2} \rfloor\) 行。

对于每一行 \(i\)，我们需要将其与对应的行 \(i_2\) 进行交换，其中 \(i_2 = x + k - 1 - (i - x)\)。

在交换时，我们需要遍历 \(j \in [y, y + k)\)，将 \(\text{grid}[i][j]\) 和 \(\text{grid}[i_2][j]\) 进行交换。

最后，返回更新后的矩阵。

时间复杂度 \(O(k^2)\)，其中 \(k\) 是子矩阵的边长。空间复杂度 \(O(1)\)。

1
2
3
4
5
6
7
8
9
class Solution:
    def reverseSubmatrix(
        self, grid: List[List[int]], x: int, y: int, k: int
    ) -> List[List[int]]:
        for i in range(x, x + k // 2):
            i2 = x + k - 1 - (i - x)
            for j in range(y, y + k):
                grid[i][j], grid[i2][j] = grid[i2][j], grid[i][j]
        return grid

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution {
    public int[][] reverseSubmatrix(int[][] grid, int x, int y, int k) {
        for (int i = x; i < x + k / 2; i++) {
            int i2 = x + k - 1 - (i - x);
            for (int j = y; j < y + k; j++) {
                int t = grid[i][j];
                grid[i][j] = grid[i2][j];
                grid[i2][j] = t;
            }
        }
        return grid;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
public:
    vector<vector<int>> reverseSubmatrix(vector<vector<int>>& grid, int x, int y, int k) {
        for (int i = x; i < x + k / 2; i++) {
            int i2 = x + k - 1 - (i - x);
            for (int j = y; j < y + k; j++) {
                swap(grid[i][j], grid[i2][j]);
            }
        }
        return grid;
    }
};

1
2
3
4
5
6
7
8
9
func reverseSubmatrix(grid [][]int, x int, y int, k int) [][]int {
    for i := x; i < x+k/2; i++ {
        i2 := x + k - 1 - (i - x)
        for j := y; j < y+k; j++ {
            grid[i][j], grid[i2][j] = grid[i2][j], grid[i][j]
        }
    }
    return grid
}

1
2
3
4
5
6
7
8
9
function reverseSubmatrix(grid: number[][], x: number, y: number, k: number): number[][] {
    for (let i = x; i < x + Math.floor(k / 2); i++) {
        const i2 = x + k - 1 - (i - x);
        for (let j = y; j < y + k; j++) {
            [grid[i][j], grid[i2][j]] = [grid[i2][j], grid[i][j]];
        }
    }
    return grid;
}

评论