


题目描述
给你一个大小为 n x m 的二维整数矩阵 grid,其中每个元素的值为 0、1 或 2。
V 形对角线段 定义如下:
- 线段从
1 开始。 - 后续元素按照以下无限序列的模式排列:
2, 0, 2, 0, ...。 - 该线段:
- 起始于某个对角方向(左上到右下、右下到左上、右上到左下或左下到右上)。
- 沿着相同的对角方向继续,保持 序列模式 。
- 在保持 序列模式 的前提下,最多允许 一次顺时针 90 度转向 另一个对角方向。
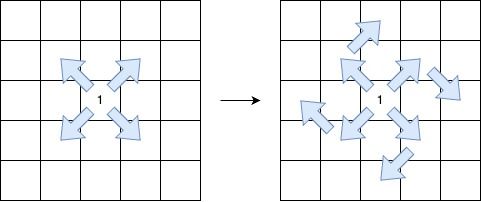
返回最长的 V 形对角线段 的 长度 。如果不存在有效的线段,则返回 0。
示例 1:
输入: grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]
输出: 5
解释:
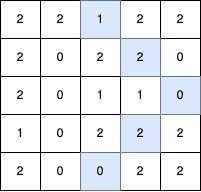
最长的 V 形对角线段长度为 5,路径如下:(0,2) → (1,3) → (2,4),在 (2,4) 处进行 顺时针 90 度转向 ,继续路径为 (3,3) → (4,2)。
示例 2:
输入: grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]
输出: 4
解释:
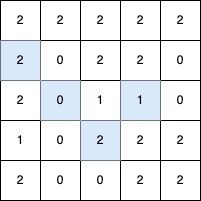
最长的 V 形对角线段长度为 4,路径如下:(2,3) → (3,2),在 (3,2) 处进行 顺时针 90 度转向 ,继续路径为 (2,1) → (1,0)。
示例 3:
输入: grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]
输出: 5
解释:
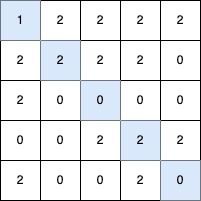
最长的 V 形对角线段长度为 5,路径如下:(0,0) → (1,1) → (2,2) → (3,3) → (4,4)。
示例 4:
输入: grid = [[1]]
输出: 1
解释:
最长的 V 形对角线段长度为 1,路径如下:(0,0)。
提示:
n == grid.lengthm == grid[i].length1 <= n, m <= 500grid[i][j] 的值为 0、1 或 2。
解法
方法一:记忆化搜索
我们设计一个函数 \(\text{dfs}(i, j, k, \textit{cnt})\),表示上一个位置为 \((i, j)\),当前方向为 \(k\),剩余可转向次数为 \(\textit{cnt}\) 时,返回最长的 V 形对角线段长度。
函数 \(\text{dfs}\) 的执行逻辑如下:
我们首先基于上一个位置以及当前的方向,计算当前得到当前位置 \((x, y)\),然后计算当前目标值 \(\textit{target}\)。如果 \(x\) 或 \(y\) 不在矩阵范围内,或者 \(\textit{grid}[x][y] \neq \textit{target}\),返回 \(0\)。
否则,我们有两种选择:
- 继续沿着当前方向前进。
- 在当前位置进行顺时针 90 度转向,然后继续前进。
我们可以通过改变方向来实现顺时针 90 度转向。具体来说,如果当前方向为 \(k\),则顺时针 90 度转向后的新方向为 \((k + 1) \bmod 4\)。最后,我们选择这两种选择中的最大值作为当前状态的结果。
在主函数中,我们遍历整个矩阵,对于每个值为 1 的位置,尝试四个方向的搜索,并更新答案。
遍历结束后,返回答案即可。
为了避免重复计算,我们使用记忆化搜索来缓存中间结果。
时间复杂度 \(O(m \times n)\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | class Solution:
def lenOfVDiagonal(self, grid: List[List[int]]) -> int:
@cache
def dfs(i: int, j: int, k: int, cnt: int) -> int:
x, y = i + dirs[k], j + dirs[k + 1]
target = 2 if grid[i][j] == 1 else (2 - grid[i][j])
if not 0 <= x < m or not 0 <= y < n or grid[x][y] != target:
return 0
res = dfs(x, y, k, cnt)
if cnt > 0:
res = max(res, dfs(x, y, (k + 1) % 4, 0))
return 1 + res
m, n = len(grid), len(grid[0])
dirs = (1, 1, -1, -1, 1)
ans = 0
for i, row in enumerate(grid):
for j, x in enumerate(row):
if x == 1:
for k in range(4):
ans = max(ans, dfs(i, j, k, 1) + 1)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | class Solution {
private int m, n;
private final int[] dirs = {1, 1, -1, -1, 1};
private Integer[][][][] f;
public int lenOfVDiagonal(int[][] grid) {
m = grid.length;
n = grid[0].length;
f = new Integer[m][n][4][2];
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
for (int k = 0; k < 4; k++) {
ans = Math.max(ans, dfs(grid, i, j, k, 1) + 1);
}
}
}
}
return ans;
}
private int dfs(int[][] grid, int i, int j, int k, int cnt) {
if (f[i][j][k][cnt] != null) {
return f[i][j][k][cnt];
}
int x = i + dirs[k];
int y = j + dirs[k + 1];
int target = grid[i][j] == 1 ? 2 : (2 - grid[i][j]);
if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y] != target) {
f[i][j][k][cnt] = 0;
return 0;
}
int res = dfs(grid, x, y, k, cnt);
if (cnt > 0) {
res = Math.max(res, dfs(grid, x, y, (k + 1) % 4, 0));
}
f[i][j][k][cnt] = 1 + res;
return 1 + res;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 | class Solution {
public:
static constexpr int MAXN = 501;
int f[MAXN][MAXN][4][2];
int lenOfVDiagonal(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int dirs[5] = {1, 1, -1, -1, 1};
memset(f, -1, sizeof(f));
auto dfs = [&](this auto&& dfs, int i, int j, int k, int cnt) -> int {
if (f[i][j][k][cnt] != -1) {
return f[i][j][k][cnt];
}
int x = i + dirs[k];
int y = j + dirs[k + 1];
int target = grid[i][j] == 1 ? 2 : (2 - grid[i][j]);
if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y] != target) {
f[i][j][k][cnt] = 0;
return 0;
}
int res = dfs(x, y, k, cnt);
if (cnt > 0) {
res = max(res, dfs(x, y, (k + 1) % 4, 0));
}
f[i][j][k][cnt] = 1 + res;
return 1 + res;
};
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
for (int k = 0; k < 4; ++k) {
ans = max(ans, dfs(i, j, k, 1) + 1);
}
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49 | func lenOfVDiagonal(grid [][]int) int {
m, n := len(grid), len(grid[0])
dirs := []int{1, 1, -1, -1, 1}
f := make([][][4][2]int, m)
for i := range f {
f[i] = make([][4][2]int, n)
}
var dfs func(i, j, k, cnt int) int
dfs = func(i, j, k, cnt int) int {
if f[i][j][k][cnt] != 0 {
return f[i][j][k][cnt]
}
x := i + dirs[k]
y := j + dirs[k+1]
var target int
if grid[i][j] == 1 {
target = 2
} else {
target = 2 - grid[i][j]
}
if x < 0 || x >= m || y < 0 || y >= n || grid[x][y] != target {
f[i][j][k][cnt] = 0
return 0
}
res := dfs(x, y, k, cnt)
if cnt > 0 {
res = max(res, dfs(x, y, (k+1)%4, 0))
}
f[i][j][k][cnt] = res + 1
return res + 1
}
ans := 0
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if grid[i][j] == 1 {
for k := 0; k < 4; k++ {
ans = max(ans, dfs(i, j, k, 1)+1)
}
}
}
}
return ans
}
|






