双指针 图 并查集 排序 数组
题目描述 给你一个 n 个点组成的无向图边集 edgeList ,其中 edgeList[i] = [ui , vi , disi ] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意,两个点之间可能有 超过一条边 。
给你一个查询数组queries ,其中 queries[j] = [pj , qj , limitj ] ,你的任务是对于每个查询 queries[j] ,判断是否存在从 pj 到 qj 的路径,且这条路径上的每一条边都 严格小于 limitj 。
请你返回一个 布尔数组 answer ,其中 answer.length == queries.length ,当 queries[j] 的查询结果为 true 时, answer 第 j 个值为 true ,否则为 false 。
示例 1:
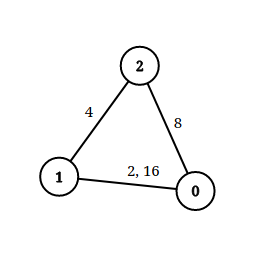
输入: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出: [false,true]
解释: 上图为给定的输入数据。注意到 0 和 1 之间有两条重边,分别为 2 和 16 。
对于第一个查询,0 和 1 之间没有小于 2 的边,所以我们返回 false 。
对于第二个查询,有一条路径(0 -> 1 -> 2)两条边都小于 5 ,所以这个查询我们返回 true 。
示例 2:
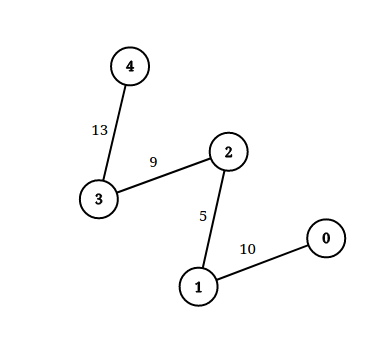
输入: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
输出: [true,false]
解释: 上图为给定数据。
提示:
2 <= n <= 105 1 <= edgeList.length, queries.length <= 105 edgeList[i].length == 3queries[j].length == 30 <= ui , vi , pj , qj <= n - 1ui != vi pj != qj 1 <= disi , limitj <= 109 两个点之间可能有 多条 边。 解法 方法一:离线查询 + 并查集 根据题目要求,我们需要对每个查询 \(queries[i]\) 进行判断,即判断当前查询的两个点 \(a\) 和 \(b\) 之间是否存在一条边权小于等于 \(limit\) 的路径。
判断两点是否连通可以通过并查集来实现。另外,由于查询的顺序对结果没有影响,因此我们可以先将所有查询按照 \(limit\) 从小到大排序,所有边也按照边权从小到大排序。
然后对于每个查询,我们从边权最小的边开始,将边权严格小于 \(limit\) 的所有边加入并查集,接着利用并查集的查询操作判断两点是否连通即可。
时间复杂度 \(O(m \times \log m + q \times \log q)\) ,其中 \(m\) 和 \(q\) 分别为边数和查询数。
Python3 Java C++ Go Rust
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 class Solution :
def distanceLimitedPathsExist (
self , n : int , edgeList : List [ List [ int ]], queries : List [ List [ int ]]
) -> List [ bool ]:
def find ( x ):
if p [ x ] != x :
p [ x ] = find ( p [ x ])
return p [ x ]
p = list ( range ( n ))
edgeList . sort ( key = lambda x : x [ 2 ])
j = 0
ans = [ False ] * len ( queries )
for i , ( a , b , limit ) in sorted ( enumerate ( queries ), key = lambda x : x [ 1 ][ 2 ]):
while j < len ( edgeList ) and edgeList [ j ][ 2 ] < limit :
u , v , _ = edgeList [ j ]
p [ find ( u )] = find ( v )
j += 1
ans [ i ] = find ( a ) == find ( b )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 class Solution {
private int [] p ;
public boolean [] distanceLimitedPathsExist ( int n , int [][] edgeList , int [][] queries ) {
p = new int [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
p [ i ] = i ;
}
Arrays . sort ( edgeList , ( a , b ) -> a [ 2 ] - b [ 2 ] );
int m = queries . length ;
boolean [] ans = new boolean [ m ] ;
Integer [] qid = new Integer [ m ] ;
for ( int i = 0 ; i < m ; ++ i ) {
qid [ i ] = i ;
}
Arrays . sort ( qid , ( i , j ) -> queries [ i ][ 2 ] - queries [ j ][ 2 ] );
int j = 0 ;
for ( int i : qid ) {
int a = queries [ i ][ 0 ] , b = queries [ i ][ 1 ] , limit = queries [ i ][ 2 ] ;
while ( j < edgeList . length && edgeList [ j ][ 2 ] < limit ) {
int u = edgeList [ j ][ 0 ] , v = edgeList [ j ][ 1 ] ;
p [ find ( u ) ] = find ( v );
++ j ;
}
ans [ i ] = find ( a ) == find ( b );
}
return ans ;
}
private int find ( int x ) {
if ( p [ x ] != x ) {
p [ x ] = find ( p [ x ] );
}
return p [ x ] ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 class Solution {
public :
vector < bool > distanceLimitedPathsExist ( int n , vector < vector < int >>& edgeList , vector < vector < int >>& queries ) {
vector < int > p ( n );
iota ( p . begin (), p . end (), 0 );
sort ( edgeList . begin (), edgeList . end (), []( auto & a , auto & b ) { return a [ 2 ] < b [ 2 ]; });
function < int ( int ) > find = [ & ]( int x ) -> int {
if ( p [ x ] != x ) p [ x ] = find ( p [ x ]);
return p [ x ];
};
int m = queries . size ();
vector < bool > ans ( m );
vector < int > qid ( m );
iota ( qid . begin (), qid . end (), 0 );
sort ( qid . begin (), qid . end (), [ & ]( int i , int j ) { return queries [ i ][ 2 ] < queries [ j ][ 2 ]; });
int j = 0 ;
for ( int i : qid ) {
int a = queries [ i ][ 0 ], b = queries [ i ][ 1 ], limit = queries [ i ][ 2 ];
while ( j < edgeList . size () && edgeList [ j ][ 2 ] < limit ) {
int u = edgeList [ j ][ 0 ], v = edgeList [ j ][ 1 ];
p [ find ( u )] = find ( v );
++ j ;
}
ans [ i ] = find ( a ) == find ( b );
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 func distanceLimitedPathsExist ( n int , edgeList [][] int , queries [][] int ) [] bool {
p := make ([] int , n )
for i := range p {
p [ i ] = i
}
sort . Slice ( edgeList , func ( i , j int ) bool { return edgeList [ i ][ 2 ] < edgeList [ j ][ 2 ] })
var find func ( int ) int
find = func ( x int ) int {
if p [ x ] != x {
p [ x ] = find ( p [ x ])
}
return p [ x ]
}
m := len ( queries )
qid := make ([] int , m )
ans := make ([] bool , m )
for i := range qid {
qid [ i ] = i
}
sort . Slice ( qid , func ( i , j int ) bool { return queries [ qid [ i ]][ 2 ] < queries [ qid [ j ]][ 2 ] })
j := 0
for _ , i := range qid {
a , b , limit := queries [ i ][ 0 ], queries [ i ][ 1 ], queries [ i ][ 2 ]
for j < len ( edgeList ) && edgeList [ j ][ 2 ] < limit {
u , v := edgeList [ j ][ 0 ], edgeList [ j ][ 1 ]
p [ find ( u )] = find ( v )
j ++
}
ans [ i ] = find ( a ) == find ( b )
}
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72 impl Solution {
#[allow(dead_code)]
pub fn distance_limited_paths_exist (
n : i32 ,
edge_list : Vec < Vec < i32 >> ,
queries : Vec < Vec < i32 >> ,
) -> Vec < bool > {
let mut disjoint_set : Vec < usize > = vec! [ 0 ; n as usize ];
let mut ans_vec : Vec < bool > = vec! [ false ; queries . len ()];
let mut q_vec : Vec < usize > = vec! [ 0 ; queries . len ()];
// Initialize the set
for i in 0 .. n {
disjoint_set [ i as usize ] = i as usize ;
}
// Initialize the q_vec
for i in 0 .. queries . len () {
q_vec [ i ] = i ;
}
// Sort the q_vec based on the query limit, from the lowest to highest
q_vec . sort_by ( | i , j | queries [ * i ][ 2 ]. cmp ( & queries [ * j ][ 2 ]));
// Sort the edge_list based on the edge weight, from the lowest to highest
let mut edge_list = edge_list . clone ();
edge_list . sort_by ( | i , j | i [ 2 ]. cmp ( & j [ 2 ]));
let mut edge_idx : usize = 0 ;
for q_idx in & q_vec {
let s = queries [ * q_idx ][ 0 ] as usize ;
let d = queries [ * q_idx ][ 1 ] as usize ;
let limit = queries [ * q_idx ][ 2 ];
// Construct the disjoint set
while edge_idx < edge_list . len () && edge_list [ edge_idx ][ 2 ] < limit {
Solution :: union (
edge_list [ edge_idx ][ 0 ] as usize ,
edge_list [ edge_idx ][ 1 ] as usize ,
& mut disjoint_set ,
);
edge_idx += 1 ;
}
// If the parents of s & d are the same, this query should be `true`
// Otherwise, the current query is `false`
ans_vec [ * q_idx ] = Solution :: check_valid ( s , d , & mut disjoint_set );
}
ans_vec
}
#[allow(dead_code)]
pub fn find ( x : usize , d_set : & mut Vec < usize > ) -> usize {
if d_set [ x ] != x {
d_set [ x ] = Solution :: find ( d_set [ x ], d_set );
}
return d_set [ x ];
}
#[allow(dead_code)]
pub fn union ( s : usize , d : usize , d_set : & mut Vec < usize > ) {
let p_s = Solution :: find ( s , d_set );
let p_d = Solution :: find ( d , d_set );
d_set [ p_s ] = p_d ;
}
#[allow(dead_code)]
pub fn check_valid ( s : usize , d : usize , d_set : & mut Vec < usize > ) -> bool {
let p_s = Solution :: find ( s , d_set );
let p_d = Solution :: find ( d , d_set );
p_s == p_d
}
}
附并查集相关介绍以及常用模板:
并查集是一种树形的数据结构,顾名思义,它用于处理一些不交集的合并 及查询 问题。 它支持两种操作:
查找(Find):确定某个元素处于哪个子集,单次操作时间复杂度 \(O(\alpha(n))\) 合并(Union):将两个子集合并成一个集合,单次操作时间复杂度 \(O(\alpha(n))\) 其中 \(\alpha\) 为阿克曼函数的反函数,其增长极其缓慢,也就是说其单次操作的平均运行时间可以认为是一个很小的常数。
以下是并查集的常用模板,需要熟练掌握。其中:
n 表示节点数p 存储每个点的父节点,初始时每个点的父节点都是自己size 只有当节点是祖宗节点时才有意义,表示祖宗节点所在集合中,点的数量find(x) 函数用于查找 \(x\) 所在集合的祖宗节点union(a, b) 函数用于合并 \(a\) 和 \(b\) 所在的集合 Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 p = list ( range ( n ))
size = [ 1 ] * n
def find ( x ):
if p [ x ] != x :
# 路径压缩
p [ x ] = find ( p [ x ])
return p [ x ]
def union ( a , b ):
pa , pb = find ( a ), find ( b )
if pa == pb :
return
p [ pa ] = pb
size [ pb ] += size [ pa ]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 int [] p = new int [ n ] ;
int [] size = new int [ n ] ;
for ( int i = 0 ; i < n ; ++ i ) {
p [ i ] = i ;
size [ i ] = 1 ;
}
int find ( int x ) {
if ( p [ x ] != x ) {
// 路径压缩
p [ x ] = find ( p [ x ] );
}
return p [ x ] ;
}
void union ( int a , int b ) {
int pa = find ( a ), pb = find ( b );
if ( pa == pb ) {
return ;
}
p [ pa ] = pb ;
size [ pb ] += size [ pa ] ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 vector < int > p ( n );
iota ( p . begin (), p . end (), 0 );
vector < int > size ( n , 1 );
int find ( int x ) {
if ( p [ x ] != x ) {
// 路径压缩
p [ x ] = find ( p [ x ]);
}
return p [ x ];
}
void unite ( int a , int b ) {
int pa = find ( a ), pb = find ( b );
if ( pa == pb ) return ;
p [ pa ] = pb ;
size [ pb ] += size [ pa ];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 p := make ([] int , n )
size := make ([] int , n )
for i := range p {
p [ i ] = i
size [ i ] = 1
}
func find ( x int ) int {
if p [ x ] != x {
// 路径压缩
p [ x ] = find ( p [ x ])
}
return p [ x ]
}
func union ( a , b int ) {
pa , pb := find ( a ), find ( b )
if pa == pb {
return
}
p [ pa ] = pb
size [ pb ] += size [ pa ]
}