935. Knight Dialer

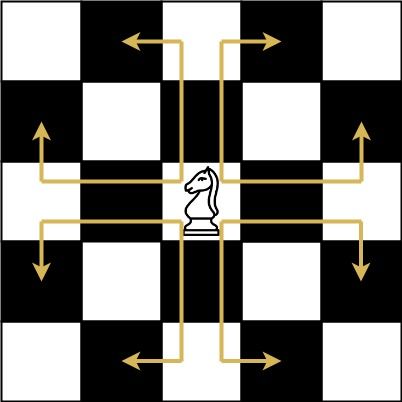
Description

The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagram:

A chess knight can move as indicated in the chess diagram below:

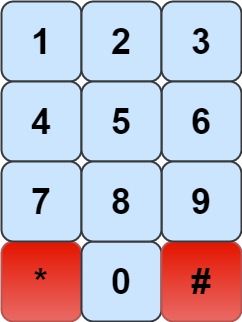
We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).

Given an integer n, return how many distinct phone numbers of length n we can dial.

You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.

As the answer may be very large, return the answer modulo 10⁹ + 7.

Example 1:

Input: n = 1
Output: 10
Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.

Example 2:

Input: n = 2
Output: 20
Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Example 3:

Input: n = 3131
Output: 136006598
Explanation: Please take care of the mod.

Constraints:

1 <= n <= 5000

Solutions

Solution 1: Recurrence

According to the problem description, we need to calculate the number of different phone numbers of length \(n\). Each digit can only follow certain fixed digits, which we can list as follows:

Current Digit	Previous Digits
0	4, 6
1	6, 8
2	7, 9
3	4, 8
4	0, 3, 9
5
6	0, 1, 7
7	2, 6
8	1, 3
9	2, 4

We can use a recurrence approach to calculate the number of different phone numbers of length \(n\). Let \(f[i]\) represent the number of different phone numbers of length \(i\). Initially, \(f[1] = 1\). For phone numbers of length \(i\), we can calculate them based on phone numbers of length \(i - 1\). Therefore, we can derive the recurrence relations:

\[ \begin{aligned} g[0] & = f[4] + f[6] \\ g[1] & = f[6] + f[8] \\ g[2] & = f[7] + f[9] \\ g[3] & = f[4] + f[8] \\ g[4] & = f[0] + f[3] + f[9] \\ g[6] & = f[0] + f[1] + f[7] \\ g[7] & = f[2] + f[6] \\ g[8] & = f[1] + f[3] \\ g[9] & = f[2] + f[4] \end{aligned} \]

Then, we update \(f\) to \(g\) and continue calculating the phone numbers of the next length until we calculate the number of phone numbers of length \(n\).

Finally, we sum all the elements in \(f\) and take the result modulo \(10^9 + 7\) to get the answer.

The time complexity is \(O(n)\), where \(n\) is the length of the phone number. The space complexity is \(O(|\Sigma|)\), where \(\Sigma\) is the set of digits, and in this problem \(|\Sigma| = 10\).

Python3JavaC++GoTypeScriptC#

class Solution:
    def knightDialer(self, n: int) -> int:
        f = [1] * 10
        for _ in range(n - 1):
            g = [0] * 10
            g[0] = f[4] + f[6]
            g[1] = f[6] + f[8]
            g[2] = f[7] + f[9]
            g[3] = f[4] + f[8]
            g[4] = f[0] + f[3] + f[9]
            g[6] = f[0] + f[1] + f[7]
            g[7] = f[2] + f[6]
            g[8] = f[1] + f[3]
            g[9] = f[2] + f[4]
            f = g
        return sum(f) % (10**9 + 7)

class Solution {
    public int knightDialer(int n) {
        final int mod = (int) 1e9 + 7;
        long[] f = new long[10];
        Arrays.fill(f, 1);
        while (--n > 0) {
            long[] g = new long[10];
            g[0] = (f[4] + f[6]) % mod;
            g[1] = (f[6] + f[8]) % mod;
            g[2] = (f[7] + f[9]) % mod;
            g[3] = (f[4] + f[8]) % mod;
            g[4] = (f[0] + f[3] + f[9]) % mod;
            g[6] = (f[0] + f[1] + f[7]) % mod;
            g[7] = (f[2] + f[6]) % mod;
            g[8] = (f[1] + f[3]) % mod;
            g[9] = (f[2] + f[4]) % mod;
            f = g;
        }
        return (int) (Arrays.stream(f).sum() % mod);
    }
}

class Solution {
public:
    int knightDialer(int n) {
        const int mod = 1e9 + 7;
        vector<long long> f(10, 1);
        while (--n) {
            vector<long long> g(10);
            g[0] = (f[4] + f[6]) % mod;
            g[1] = (f[6] + f[8]) % mod;
            g[2] = (f[7] + f[9]) % mod;
            g[3] = (f[4] + f[8]) % mod;
            g[4] = (f[0] + f[3] + f[9]) % mod;
            g[6] = (f[0] + f[1] + f[7]) % mod;
            g[7] = (f[2] + f[6]) % mod;
            g[8] = (f[1] + f[3]) % mod;
            g[9] = (f[2] + f[4]) % mod;
            f = g;
        }
        return accumulate(f.begin(), f.end(), 0LL) % mod;
    }
};

func knightDialer(n int) (ans int) {
    f := make([]int, 10)
    for i := range f {
        f[i] = 1
    }
    const mod int = 1e9 + 7
    for i := 1; i < n; i++ {
        g := make([]int, 10)
        g[0] = (f[4] + f[6]) % mod
        g[1] = (f[6] + f[8]) % mod
        g[2] = (f[7] + f[9]) % mod
        g[3] = (f[4] + f[8]) % mod
        g[4] = (f[0] + f[3] + f[9]) % mod
        g[6] = (f[0] + f[1] + f[7]) % mod
        g[7] = (f[2] + f[6]) % mod
        g[8] = (f[1] + f[3]) % mod
        g[9] = (f[2] + f[4]) % mod
        f = g
    }
    for _, x := range f {
        ans = (ans + x) % mod
    }
    return
}

function knightDialer(n: number): number {
    const mod = 1e9 + 7;
    const f: number[] = Array(10).fill(1);
    while (--n) {
        const g: number[] = Array(10).fill(0);
        g[0] = (f[4] + f[6]) % mod;
        g[1] = (f[6] + f[8]) % mod;
        g[2] = (f[7] + f[9]) % mod;
        g[3] = (f[4] + f[8]) % mod;
        g[4] = (f[0] + f[3] + f[9]) % mod;
        g[6] = (f[0] + f[1] + f[7]) % mod;
        g[7] = (f[2] + f[6]) % mod;
        g[8] = (f[1] + f[3]) % mod;
        g[9] = (f[2] + f[4]) % mod;
        f.splice(0, 10, ...g);
    }
    return f.reduce((a, b) => (a + b) % mod);
}

public class Solution {
    public int KnightDialer(int n) {
        const int mod = 1000000007;
        long[] f = new long[10];
        for (int i = 0; i < 10; i++) {
            f[i] = 1;
        }

        while (--n > 0) {
            long[] g = new long[10];
            g[0] = (f[4] + f[6]) % mod;
            g[1] = (f[6] + f[8]) % mod;
            g[2] = (f[7] + f[9]) % mod;
            g[3] = (f[4] + f[8]) % mod;
            g[4] = (f[0] + f[3] + f[9]) % mod;
            g[6] = (f[0] + f[1] + f[7]) % mod;
            g[7] = (f[2] + f[6]) % mod;
            g[8] = (f[1] + f[3]) % mod;
            g[9] = (f[2] + f[4]) % mod;
            f = g;
        }

        return (int)(f.Sum() % mod);
    }
}

Solution 2: Matrix Exponentiation to Accelerate Recurrence

Let's denote \(T(n)\) as a \(1 \times 10\) matrix \(\begin{bmatrix} F_0 & F_1 & F_2 \cdots F_9 \end{bmatrix}\), where \(F_i\) represents the number of phone numbers ending with digit \(i\). We want to derive \(T(n)\) from \(T(n - 1)\). In other words, we need a matrix \(\textit{base}\) such that \(T(n - 1) \times \textit{base} = T(n)\), i.e.:

\[ \begin{bmatrix} F_0 & F_1 & F_2 \cdots F_9 \end{bmatrix} \times \textit{base} = \begin{bmatrix} F_0' & F_1' & F_2' \cdots F_9' \end{bmatrix} \]

Since \(F_i' = \sum_{j} F_j\), where \(j\) is the previous digit of \(i\), the first column of the matrix \(\textit{base}\) is:

\[ \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} \]

Similarly, we can derive the entire matrix \(\textit{base}\) as follows:

\[ \begin{bmatrix} 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \]

We define the initial matrix \(res = \begin{bmatrix} 1 & 1 & 1 \cdots 1 \end{bmatrix}\), and multiply it by the matrix \(\textit{base}\) raised to the power of \(n - 1\) to obtain \(T(n)\). Finally, we sum all elements in \(T(n)\) and take the result modulo \(10^9 + 7\) to get the answer. The matrix \(\textit{base}^{n - 1}\) can be computed using matrix exponentiation, which has a time complexity of \(O(\log n)\).

The time complexity is \(O(\log n)\), and the space complexity is \(O(|\Sigma|^2)\), where \(\Sigma\) is the set of digits, and in this problem \(|\Sigma| = 10\).